角格点三角形
Mon, 25th November 2019Edit on Githubgeometrytrianglecombination
摘要
wayne发现了一篇讨论三角形角格点问题 的文章,其中要求找出所以三个角都是10°的整数倍的,而且在三角形内部可以找到一个点P 使得的三个角都是10°的整数倍。
wayne把问题进行了推广 :三角形的三个内角的比例 使得都是整数;
而且三角形ABC内部存在一点P,使得的三个内角比例也都是整数,试问这样的三角形内有多少个这样的内点?
另外由于对于等腰三角形,P在其对称轴上时通常会有很多平凡解,我们又通常会淘汰这种情况。
比较有意思的是mathe最后利用正n边形对角线交点问题 的结果给这个问题的推广情况一种公式解。
详细内容
整数度数解
chyanog首先给出所有角度都是整数度数的倍数时解的数目是5257个(而限定角度是10°的倍数时为61个);不考虑等腰三角形对称轴上的点是3275个(限定角度为10°的倍数为45个)。
比如下图为他找出的几个特殊结果:
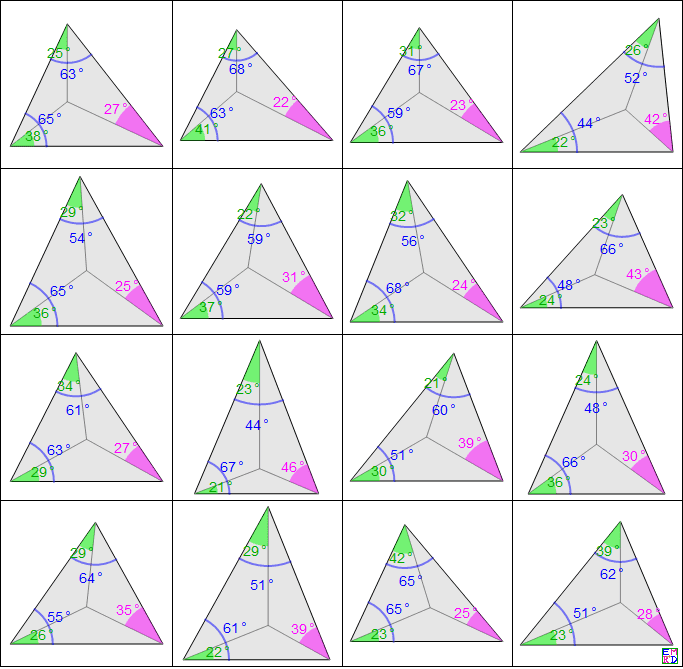
而对于一般情况的这种三角形,如下图
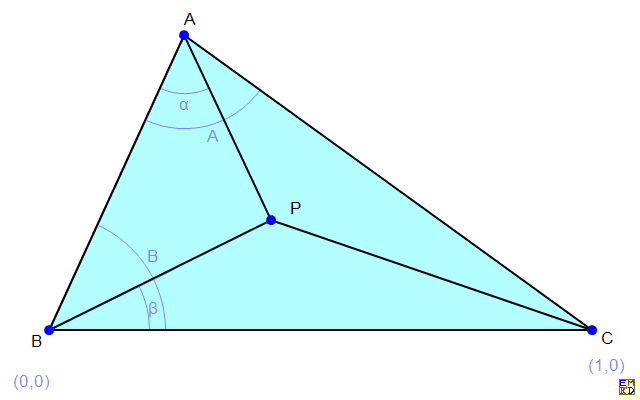
他给出了对应的mathematica代码来计数:
Clear[func];
func=Compile[{{A,_Integer}},
Module[{bag=Internal`Bag[Rest@{0}],angle},
Do[
If[A+B>=180,Continue[]];
angle=180+ArcTan[Cos[(A-α)°] Sin[(A+B)°] Sin[(B-β)°]-Sin[B °] Sin[(B+α-β)°],-Sin[(A+B)°] Sin[(A-α)°] Sin[(B-β)°]]/°;
If[0<angle<180-A-B&&0<angle<180&&Abs[Round[angle]-angle]<10^-10,Internal`StuffBag[bag,{A,α,B,β,180-A-B,Round@angle},1]];
,{B,179},{α,A},{β,B}];
Internal`BagPart[bag,All]
],
CompilationTarget->"C",RuntimeOptions->"Speed",RuntimeAttributes->{Listable}
];
Dimensions[data=Join@@(Partition[#,6]&/@func[Range[179]])]//AbsoluteTiming
Dimensions[res1=DeleteDuplicatesBy[data,Sort[Partition[#,2]]&]]
Dimensions[res2=Select[res1,DuplicateFreeQ[Sort[{#-#2,#2}]&@@@Partition[#,2]]&]]
Dimensions[res3=Select[res2,AllTrue[Divisible[#,10]&]]]与正n边形对角线交点问题的关联
mathe建议重新描述本题推广情况为:
我们可以改为要求找出所有这些角弧度都是的倍数时的数目,很显然,n不小于6才有解。
然后他采用如图记号
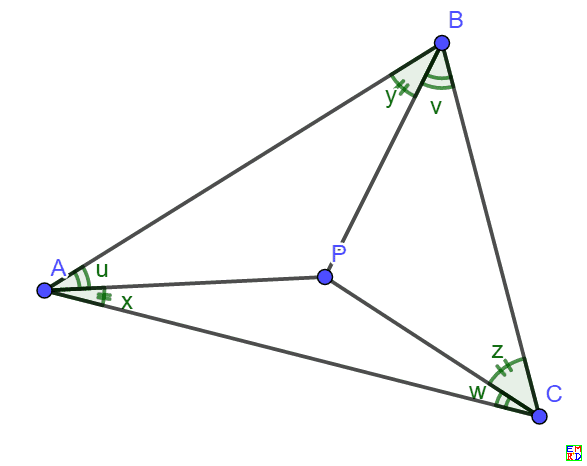
我们要求都是的正整数倍,
由于等,我们可以得出.
而这个正好是存在点P的充分必要条件。
比较有意思的是,对于任意一个合法的解,我们任意交换x,y,z的位置或u,v,w的位置还是合法的解。
非常有意思的是正n边形对角线交点问题 正好求解的是完全相同的等式。
而那个问题结果可以在A006600 找到。

其中论文 中定理4给出了完整的解,如下:
i) {u,v,w}={x,y,z} (当然)
ii)
{u,v,w}={}, {x,y,z}={}
{u,v,w}={}, {x,y,z}={}
{u,v,w}={},{x,y,z}={}
{u,v,w}={},{x,y,z}={}
iii)表格四种65组解(需要注意u,v,w任意交换或x,y,z任意交换也构成解,其中)
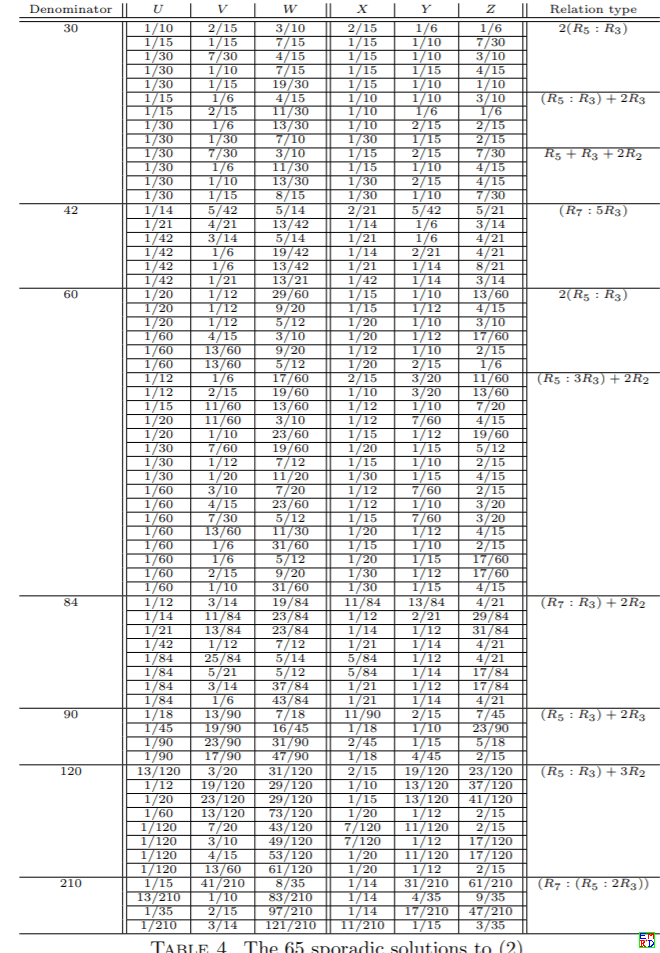
并且上面解中,唯一出现重复的解是第二类中
第二条方程时退化成第一类解
第一条和第四条方程在时相等
第二条和第四条方程在时相等。
经过复杂的分析,mathe最后得出所有角弧度为的倍数时的数目可以写成
于是
对于15°角倍数情况对应n=12,结果为13
对于10°角倍数情况对应n=18,结果为61
对于3°角倍数情况对应n=60,结果为1045
对于整数角度情况对应n=180,结果是5257
wayne问题计数的最大值
mathe注意到wayne问的其实和大家讨论的是不同的问题。wanye的问题是给定一个三个角都是有理度数的三角形,其内部有多少个满足条件的P点。当然在三角形为等腰三角形时,其对称轴上可以有无穷多个点, 使得它分割的三个小三角形的角都是有理度数。但是对于非等腰三角形(或者等腰三角形去除对称轴上的点),总是有而且只有有限个点满足条件。其中,每个三角形通常至少有三个第一类点,分别为角平分线交点和前面提到第一类一对共轭点(但是对于正三角形三个点重合)。而只有极少数三角形会拥有第二类和第三类点。所以对于给定的三角形,计算满足条件的所有P点也不能难,按上面公式逐一匹配即可。但是我们还有一个问题,非等腰三角形最多可以拥有几个满足条件的P点?等腰三角形最多可以拥有多少个不在对称轴上的满足条件的P点。
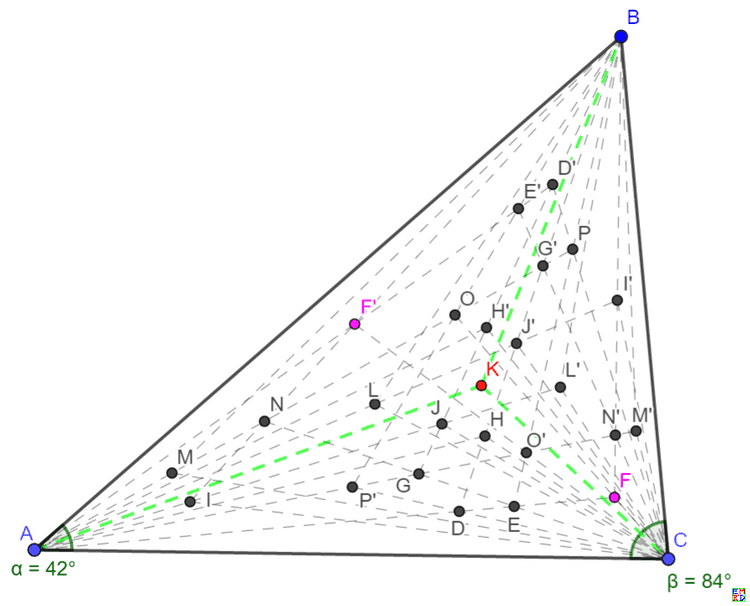
最终mathe计算得知非等腰三角形最多有25个满足条件的P点:
Triangle: {7/30,3/10,7/15} has 25 rational angle points
{1/30,1/6,2/5:1/5,2/15,1/15}
{1/30,1/5,11/30:1/5,1/10,1/10}
{1/30,4/15,1/5:7/60,3/20,7/30}
{1/15,1/10,2/5:1/6,1/5,1/15}
{1/15,2/15,11/30:1/6,1/6,1/10}
{1/15,1/5,4/15:1/6,1/10,1/5}
{1/15,4/15,1/10:1/6,1/30,11/30}
{1/15,17/60,1/20:1/6,1/60,5/12}
{1/12,1/6,17/60:3/20,2/15,11/60}
{1/10,1/30,13/30:2/15,4/15,1/30}
{1/10,2/15,3/10:2/15,1/6,1/6}
{1/10,13/60,3/20:2/15,1/12,19/60}
{7/60,3/20,7/30:7/60,3/20,7/30}
{2/15,1/12,19/60:1/10,13/60,3/20}
{2/15,1/6,1/6:1/10,2/15,3/10}
{2/15,4/15,1/30:1/10,1/30,13/30}
{3/20,2/15,11/60:1/12,1/6,17/60}
{1/6,1/60,5/12:1/15,17/60,1/20}
{1/6,1/30,11/30:1/15,4/15,1/10}
{1/6,1/10,1/5:1/15,1/5,4/15}
{1/6,1/6,1/10:1/15,2/15,11/30}
{1/6,1/5,1/15:1/15,1/10,2/5}
{1/5,1/30,4/15:7/60,3/20,7/30}
{1/5,1/10,1/10:1/30,1/5,11/30}
{1/5,2/15,1/15:1/30,1/6,2/5}
而chyanog最早发现等腰三角形可以有24个满足条件的非对称轴上P点,并且mathe的代码验证了这是最多的情况:
Triangle: {1/5,1/5,3/5} has 24 rational angle points
201(t=1/60){1/60,1/6,9/20:11/60,1/30,3/20}
202(t=1/15){1/30,1/15,17/30:1/6,2/15,1/30}
202(t=1/30){1/30,1/10,8/15:1/6,1/10,1/15}
200(t=2/15){1/30,2/15,7/15:1/6,1/15,2/15}
201(t=1/60){1/30,11/60,3/20:1/6,1/60,9/20}
203(t=1/20){1/20,2/15,23/60:3/20,1/15,13/60}
202(t=1/15){1/15,1/30,17/30:2/15,1/6,1/30}
200(t=1/10){1/15,1/10,13/30:2/15,1/10,1/6}
203(t=1/20){1/15,3/20,13/60:2/15,1/20,23/60}
200(t=2/15){1/15,1/6,2/15:2/15,1/30,7/15}
202(t=1/30){1/10,1/30,8/15:1/10,1/6,1/15}
200(t=1/10){1/10,1/15,13/30:1/10,2/15,1/6}
200(t=1/10){1/10,2/15,1/6:1/10,1/15,13/30}
202(t=1/30){1/10,1/6,1/15:1/10,1/30,8/15}
200(t=2/15){2/15,1/30,7/15:1/15,1/6,2/15}
203(t=1/20){2/15,1/20,23/60:1/15,3/20,13/60}
200(t=1/10){2/15,1/10,1/6:1/15,1/10,13/30}
202(t=1/15){2/15,1/6,1/30:1/15,1/30,17/30}
203(t=1/20){3/20,1/15,13/60:1/20,2/15,23/60}
201(t=1/60){1/6,1/60,9/20:1/30,11/60,3/20}
200(t=2/15){1/6,1/15,2/15:1/30,2/15,7/15}
202(t=1/30){1/6,1/10,1/15:1/30,1/10,8/15}
202(t=1/15){1/6,2/15,1/30:1/30,1/15,17/30}
201(t=1/60){11/60,1/30,3/20:1/60,1/6,9/20}
点击下载更多格点三角形结果 。
chyanog还从网络上发现了一篇类似的文章 ,里面讨论了所有整数度数情况的格点三角形.
王守恩发现文章里面有一处小错误,其中包含了一组重复的结果,除此之外,可以和我们的方法得出完全同样的结果。
最后zeroieme也给了一段简短的mathematica代码用于解决这个问题
(Sin[Subscript[\[Theta], 1]] Sin[Subscript[\[Theta], 2]] Sin[Subscript[\[Theta], 3]])/(Sin[30\[Degree]-Subscript[\[Theta], 1]] Sin[30\[Degree]-Subscript[\[Theta], 2]] Sin[120\[Degree]-Subscript[\[Theta], 3]])/.{Subscript[\[Theta], 1]->\[Pi]/2,Subscript[\[Theta], 2]->\[Pi]/2,Subscript[\[Theta], 3]->2 ArcTan[(-5+2 Sqrt[13])/(3 Sqrt[3])]}//FunctionExpand//TrigExpand//FullSimplify