2016年10月TSC999提问：
用 m 种颜色的珠子穿手串，每串有 n 颗珠子，每种颜色的珠子都足够多。有多少种配色不同的手串？

2019年10月markfang2050提问:
某珠宝商准备将蓝、绿、紫三种不同颜色的珠子串成由七颗珠子组成的手链进行出售。请问有多少种不同排列顺序的手链产生？
注意：1，没说一定要用全三色；2，手串是环形，对称性要排除。

详细内容

七色彩珠

markfang2050给他的问题配上几个例图:

mathe手工分析markfang2050的问题:
同色3种, 如果左右对称，对称轴过一棵珠子，$3^4-3=78$种（需要去除同色的三种）, 任意摆放的去掉同色和对称的有$\frac{3^7-3-78\times 7}{14}=117$, 得出总数为$3+78+117=198$.

northwolves很快回复markfang2050,对于他的问题，n颗珠子对应的答案为:

1 3
2 6
3 10
4 21
5 39
6 92
7 198
8 498
9 1219

并且后来右给出对应的python代码并且计算到n=30:

import numpy as np
def count(n):
    m=0
    for i in range(n):
        m+=3.0**np.gcd(n,i+1)
    m+=(2+n%2)*n*3**(n//2)
    return int(m//(2*n))
for n in range(1,31):
    print (n,count(n)) 

并且指出结果和A027671匹配。

markfang2050也同样给出了Python代码, 并且指出这个问题可以用burnside引理或Polya定理高效解决。

chyanog使用Mathematica代码计算和做出所有对应的手链:

dlpg070改进chyanog的代码将数据结果和图片放在一起:

彩色手串

hujunhua指出7色手链问题是我们已经讨论过的彩珠手串的配色计数的特例。
其中，TSC999首先自己给出了一个计算结果的表格:

并且根据上面表格外推出n小于等于6时通项公式：
$S(m,2)=\frac{m(m+1)}2$
$S(m,3)=\frac{m(m^2+3m+2)}6=\frac{m(m+1)(m+2)}6$
$S(m,4)=\frac{m(m^3+2m^2+3m+2)}8=\frac{m(m+1)(m^2+m+2)}8$
$S(m,5)=\frac{m(m^4+5m^2+4)}{10}=\frac{m(m^2+1)(m^2+4)}{10}$
$S(m,6)=\frac{m(m^5+3m^3+4m^2+2m+2)}{12}=\frac{m(m+1)(m^4-m^3+4m^2+2)}{12}$
后来又给出了S(m,7), S(m,8)的公式：
$S(m,7)=\frac{m(m^6+7m^3+6)}{14}$
$S(m,8)=\frac{m(m^7+4m^4+5m^3+2m+4)}{16}$
并且给出了S(3,4)对应的所有情况的图片:

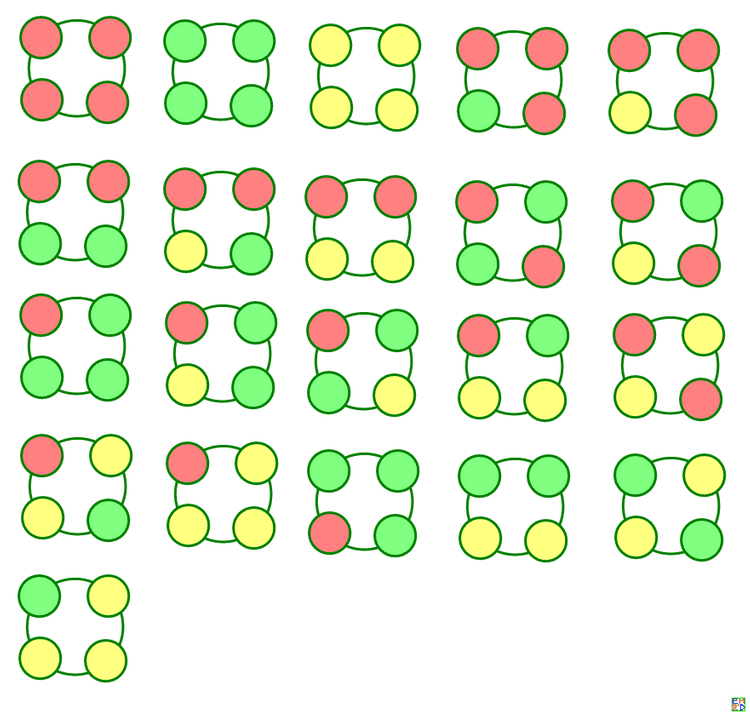
kastin给出分析:
下面内容引自 常新德 永城职业学院《有重复元素的圆排列和环排列的计数问题》:
记 $k\,(k\geqslant 1)$ 重集 $S=\{n_1\times e_1,n_2\times e_2,\cdots,n_k\times e_k\}$，其中 $e_i,\,n_i\;(i=1,2,\dots,k)$分别为元素以及相应的重复数，且集合的势 $|S|=n_1+n_2+\cdots+n_k=n$. 那么该集合所有元素的
1）圆排列数为$Q(S)=\frac{1}{n}\sum_{d|(n_1,\cdots,n_k)}\varphi(d)\frac{(\frac{n}{d})!}{\Pi_{i=1}^k(\frac{n_i}{d})!}$其中 $\varphi(x)$ 为数论中的欧拉函数，$(n_1,\cdots,n_k)$ 表示 $n_1,n_2,\cdots,n_k$ 的最大公约数。
2）环排列数为$R(S)=\frac{Q(S)+M(S)}{2}$其中，$M(S)=\frac{\left(\sum_{i=1}^k [\frac{n_i}2]\right)!}{\Pi_{i=1}^k [\frac{n_i}2]!}$ 为对称圆排列数，$[x]$ 为高斯函数（表示 $x$ 的整数部分）。
注意：环排列和圆排列，概念有细微区别。环排列考虑旋转不变且翻转不变，而圆排列考虑的是旋转不变。
现在，假定有$c$种$k$重集，那么楼主的手串总数就是$S(m,n)=\sum^m_{k=1}\sum^c_{i=1}C^k_mR(S_i)$问题分三步进行：

1. 求线性不定方程 $x_1+x_2+\cdots+x_m=n$ 的非负整数解（共 $C_{n+m-1}^{m-1}$ 组解）。
2. 对任一组解$(n_1,n_2,\cdots,n_m)$, 计算相应的重集 $S_i=\{n_1\times e_1,n_2\times e_2,\cdots,n_m\times e_m\}$的环排列数$R(S_i)$。
3. 将这些环排列数相加，$S(m,n)=\sum^c_{i=1}R(S_i)$。（这与上面的汇总公式不同，是因为这里第1步中允许$x_i$取0，$c=C_{n+m-1}^{m-1}$）
   TSC999又根据论文内容给出对应的红黄各四穿成八珠手串的漂亮图片：
   
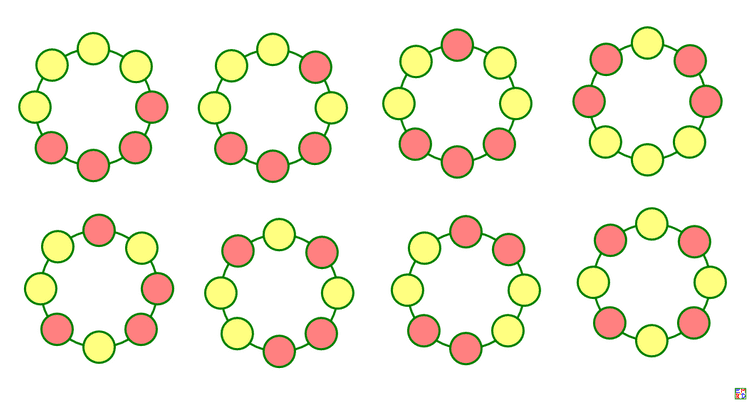
   hujunhua指出：
   可以在OEIS中找到 S(2,n)=A000029
   S(3,n)=A027671
   S(4,n)=A032275
   S(5,n)=A032276
   S(6,n)=A056341
   S(7,n)=A032276
   以及
   S(m,9)=A060561
   S(m,10)=A060562

kastin接着用伯恩赛德引理（Burnside's lemma，波利亚计数定理就是用它推导得来的）就能得到如下结论： 对于 $m$ 个颜色可重复地选取 $n$ 个排成一圈，圆排列数为$N(m,n)=\frac{1}{n}\sum_{i=1}^n m^{(n,i)}$环排列数为
$M(m,n)=\frac{N(m,n)}2+\begin{cases}\frac{m^{k+1}}{2},&n=2k+1 \\ \frac{(m+1)m^k}{4},&n=2k \end{cases}$

hujunhua 猜测对于$n$是一个奇素数$p$的情况，有$S(m,p)=\frac{m(m^{\frac{p-1}2}+p-1)(m^{\frac{p-1}2}+1)}{2p}$ .
并且得出$S(m,2p)=\frac{m\left(m^{2p-1}+p\cdot m^p+(p+1)m^{p-1}+(p-1)(m+1)\right)}{4p}$.