问题描述

求方程10^x=x^10的复数根有多少个?讨论见趣题：10^x=x^10

解答1

mathe很快给出解答:

根据儒歇定理，取$f(x)=x^{10},f(x)+g(x)=x^{10}-{10}^x$,于是在复平面中$|x|<=2$的区域里面$f(x)=0$只有10重根，所以在$|x|<=2$以内$x^{10}-{10}^x=0$也是10个根，1~3中的解和3#中解的共轭给出了所有这些结果。 而且容易看出$2<|x|<10$无解，但是对于$|x|>=10$,有无穷个解

由于过于抽象,大家反响不强烈,于是 lsr314 和wayne给出了复数解的图.

n=5;
ComplexPlot[10^x-x^10,{x,-n(1+I),n(1+I)},PlotPoints->400,Mesh->{Range[0,0],Range[0,0]},MeshFunctions->{Re[#2]&,Im[#2]&},MeshStyle->{Directive[Thickness[.005],Red],Directive[Dashed,Thickness[.005],Blue]},RegionFunction->Function[{z,f},Abs[f]<=n],BoundaryStyle->None,MeshShading->{{LightGray,White},{White, LightGray}},Epilog->{Thickness[.0001],Dashed,Circle[]},Frame->False,Axes->True]

$|x|<2$的情况下的根

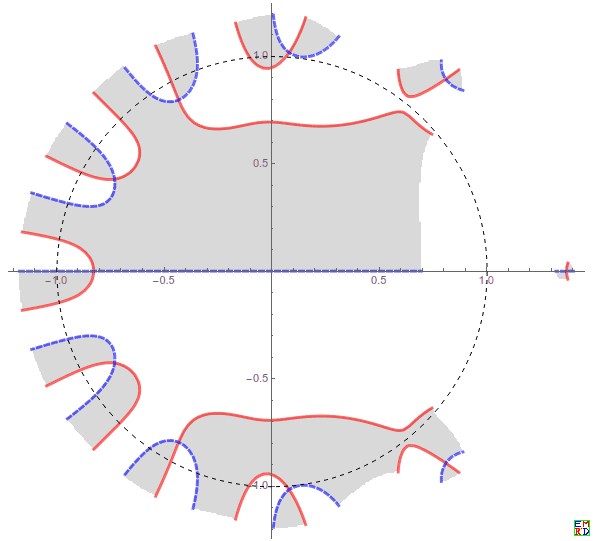
$|x|>10$的情况下的根

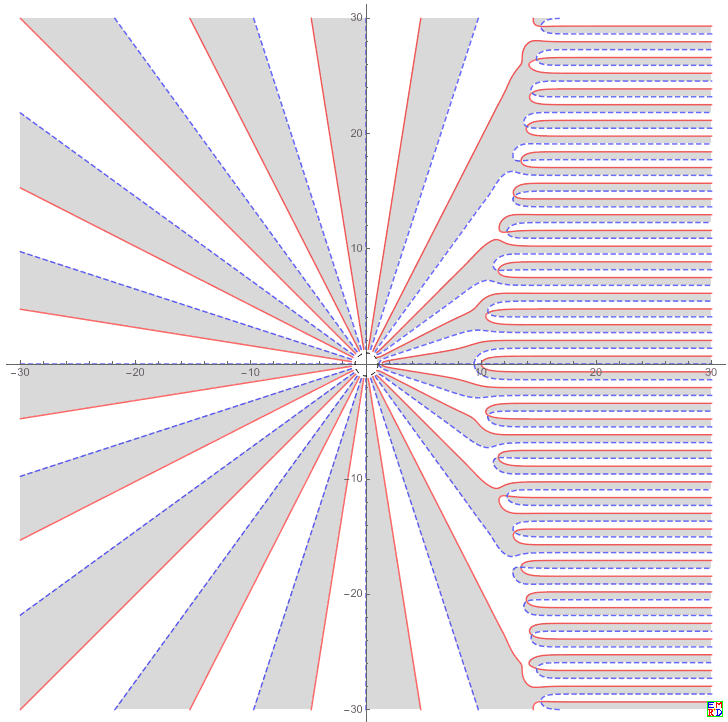
解答2

最后wayne经过一番折腾,给出了一种新的解答形式:

本题$z^a=a^z$的解 即解方程组 $r \cos\theta \ln a = a\ln r , r \sin\theta \ln a=a\theta+2n\pi$ 消元,那么得到 通解形式是: $z = \frac{a \theta +2 \pi n }{\ln a}(\cot\theta+i), n\in Z, n \neq 0$,其中 $\ln (\frac{a \theta +2 \pi n}{\ln a\sin\theta})=\frac{a \theta +2 \pi n}{a \tan \theta }$