问题起源

2009年11月， KeyTo9_Fans提问:
把平面的第一象限分割成单位小方块，把坐标(整数部分)互质的点染成黑色，其余为白色。
其效果如下图所示。（一个像素点是一个单位小方块，共1024*1024个像素，原点在左上角）

问题一（经典问题）：

在$[1,n]\times [1,n](n\to\infty)$的范围内，黑色方块所占的比例是否有极限？如何求这个极限值？

问题二（自编问题）：

考虑无限大的范围，能在里面找到大小为n*n的纯白色区域的n的最大值是多少？

问题三（自编问题）：

设想整个平面是一块黑布，我们挖去了坐标(整数部分)不互质的部分，然后把这块布“拎”起来。
这样，与主体失去连接的一些黑色方块会自动脱落，留下空洞。（用画板里的填充工具把上图的(1,1)填充一下就会发现有些黑色方块并没有被填充）
问对角线旁边的方块（坐标为(x,x+1)或(x+1,x)的方块）是否全部与(1,1)相连？请证明或找反例。

问题一证明

northwolves回复认为第一个问题的答案是$\frac6{\pi^2}$, 并且说这个问题他以前在CSDN上讨论过.
KeyTo9_Fans提供了他的思路:
P(N)有一个准确的上界：
我们只取$p_1,p_2,\dots,p_n$。
其中，$(p_1p_2\dots p_n)^2\lt N$
记$M=\sqrt{N}$，取下整。
记$T=p_1p_2\dots p_n$
那么k关于素数$p_1$、$p_2$、... 、$p_n$的余数在k=1到k=N之内至少完成了M个周期的变化。
在一个周期T里面，P(T)严格等于
$\frac{p1^2-1}{p1^2}\frac{p2^2-1}{p2^2}\dots\frac{p_n^2-1}{p_n^2}$
虽然至少完整地跑完了M个周期，但第(M+1)个周期并不完整。
（实际上可能不止M个完整的周期，但讨论的是上界，就放缩到$\frac M{M+1}$好了）
由于讨论的是上界，所以不完整的部分认为全满，一个空洞也没有。

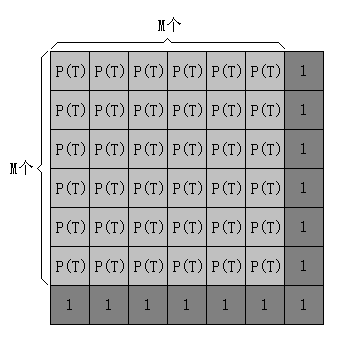
所以$P(N)\le \frac{P(T)M^2+2M+1}{(M+1)^2} \le \frac{P(T)M^2+3M}{M^2+2M}=\frac{P(T)M+3}{M+2}<P(T)+\frac1M$.
所以随着N的增大，这个上界单调递减。
另一方面，P(N)有一个准确的下界：
不完整的部分被清得一个不剩。
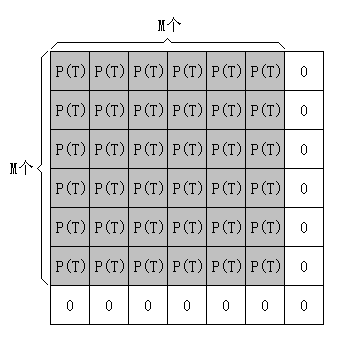
所以$P(N)\gt P(T)\frac{M^2}{(M+1)^2} - \dots \gt P(T)\frac{M^2}{(M^2+3M)} - \dots =\frac{P(T)M}{M+3}-\dots \gt P(T)-\frac3M-\dots$
除此之外，还要考虑剩下的素数
p(n+1)、p(n+2)、......
的影响。 在N*N的范围内，素数p造成的空洞不多于$\frac Np \times \frac Np$个，所占比例不多于$\frac 1{p^2}$。
我们假设剩下的素数造成的空洞与之前的素数完全不重叠。 所以P(N)大于 $P(T) - \frac3M - \frac1{{p^{\prime}}_1^2} - \frac1{{p^{\prime}}_2^2} - \frac1{{p^{\prime}}_3^2} - \dots$
其中 $p'_1$表示$p_{n+1}$，$p'_2$表示$p_{n+2}$，……，依次类推。
记 $S = \frac1{{p^{\prime}}_1^2} + \frac1{{p^{\prime}}_2^2} + \frac1{{p^{\prime}}_3^2} + \dots$
则$P(N)\gt P(T) - \frac3 M - S$
综上： $P(T) - \frac 3M - S \lt P(N) \lt P(T) + \frac 1M$
由极限的夹逼性，P(N)的极限与P(T)的极限相同, 由此在根据前面一些结论可以得出结果。

后来KeyTo9_Fans发现数学吧cqhm关于这个问题给了个很漂亮而且非常简单的证明:
R·查特在1904年发现，两个随意写出的数中，互素的概率为$\frac6{\pi^2}$。
证明:考虑两个正整数最大公约数为n的概率，记为p(n)。
明显两个数最大公约数为n当且仅当它们从n的倍数中选取且它们除以n的商互素。
因此$p(n)=\frac{p(1)}{n^2}$.
而显然所有p(n)之和为1，因为两个数有唯一的最大公约数，故p(1)乘以所有正整数平方倒数和为1,而这个和为$\frac{\pi^2}6$，故$p(1)=\frac6{\pi^2}$.
mathe评论说如果一定要给这个证明鸡蛋挑骨头，那么就是没有证明概率的存在性。

问题二讨论

mathe说问题二中纯白色正方形区域可以任意大：
取前$n^2$个素数排成$n\times n$方阵。
设方阵中每行n个数乘积为$u_i$,每列n个数乘积为$v_i$
那么所有的$u_i$之间互素，同样所有$v_i$之间互素。
根据中国剩余定理
$x\equiv -(i-1) (mod u_i) ,1\le i\le n$有解.
同样:
$y\equiv -(i-1) (mod v_i), 1\le i\le n$有解. 方阵$[x,x+n-1]\times[y,y+n-1]$满足条件.

问题三反例

问题三看上去很像是能够成立的样子，但是后来Fans在n=2189时找出了一个反例:

上图是截至[2160,2223]*[2160,2223]区间中的互质点。
左上角坐标为(2160,2160)，右下角坐标为(2223,2223)。
黑色方块表示不与(1,1)相连，红色方块表示与(1,1)相连，白色表示不互质。

问题二深入讨论计算

关于问题二，Fans又提出了一个最优解寻找问题:
对于n=2、n=3、n=4的情况，找对应的(x,y)，使得整数对
(x,y)，(x+1,y)，...，(x+n-1,y)
(x,y+1)，(x+1,y+1)，...，(x+n-1,y+1)
............
(x,y+n-1)，(x+1,y+n-1)，...，(x+n-1,y+n-1)
均不互质。
在满足上面的条件的前提下，(x+y)的值越小越好。 看看对于n=2、n=3、n=4的情况，找出来的整数对到底有多大。

northwolves快速给出n=2： (14,20)
n=3: (1274 ,1308)
mathe建议对于更大的n只搜索特殊模式的解:
如下的结构，其中?用互素而且不小于5的素数。
6 ? 2 3
? ? ? ?
2 ? 2 ?
3 ? ? 3
然后提供了一份C代码 并且找出n=4时可以有解x=726156780,y=68838054。
随后KeyTo9_Fans找出了一组更小的解: x=7247643,y=10199370 并且给出几组类似的不错的解:
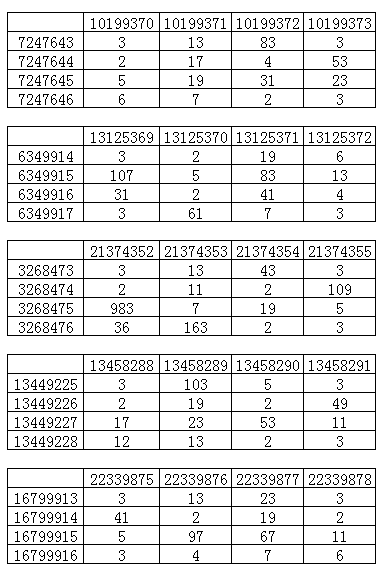并且发现已经有人捷足先登了.
Fans继续努力，程序经过通宵运行，找出n=5的解:
x=7759032126,y=247376414072

	y	y+1	y+2	y+3	y+4
x	2	3	2	41	2
x+1	137	37	103	7	11
x+2	2	19	2	29	2
x+3	23	3	109	31	3
x+4	2	47	2	5	2

x=14150396180,y=232889465522

	y	y+1	y+2	y+3	y+4
x	2	37	2	5	2
x+1	79	3	67	97	3
x+2	2	13	2	17	2
x+3	7	11	31	83	43
x+4	2	3	2	29	3

x=37945747188,y=131487690152

	y	y+1	y+2	y+3	y+4
x	2	3	2	73	2
x+1	7	41	277	151	109
x+2	2	89	2	5	2
x+3	31	3	83	19	3
x+4	2	17	2	409	2

其中最后一个结果最优秀并且被Fans提交到了A179594.