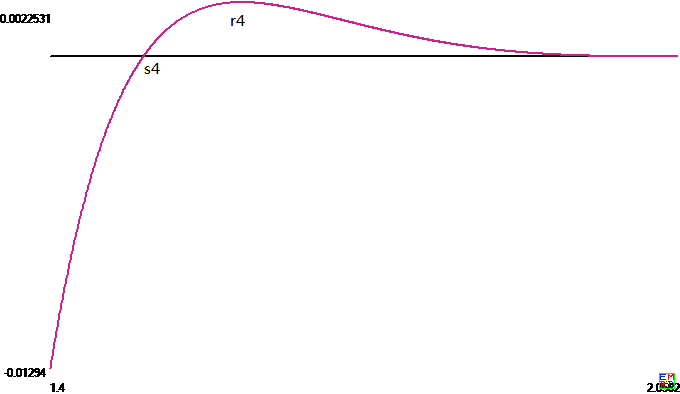摘要
mathe于2008年2月转载了陈计提出的一道不等式 a , b > 0 a,b\gt 0 a , b > 0 a + b = 4 a+b=4 a + b = 4 ( a + 1 a ) ( b + 1 b ) ≥ 25 4 (a+\frac1a)(b+\frac1b)\ge \frac{25}4 ( a + a 1 ) ( b + b 1 ) ≥ 4 2 5 a , b , c > 0 a,b,c\gt 0 a , b , c > 0 a + b + c = 6 a+b+c=6 a + b + c = 6 ( a + 1 a ) ( b + 1 b ) ( c + 1 c ) ≥ 125 8 (a+\frac1a)(b+\frac1b)(c+\frac1c)\ge \frac{125}8 ( a + a 1 ) ( b + b 1 ) ( c + c 1 ) ≥ 8 1 2 5
并且mathe希望将其推广到4个数以及更多数的一般情况。
这个不等式看上去挺简单的,在这些数都相等时取等号。但是实际上这个不等式在能够在数字相等时取等号还是挺凑巧的。
另外我们知道琴生不等式可以很好处理关于凹函数或凸函数的不等式,即只有所有变量相等时才取到极值。icesheep发现 的一个关于半凹半凸函数的不等式 可以很好的处理这里的不等式问题,并且可以处理一大批类似的不等式,比如下面这个不等式 也可以用类似方法来出来.x y z = 1 xyz=1 x y z = 1 1 ( 1 + x ) 2 + 1 ( 1 + y ) 2 + 1 ( 1 + z ) 2 ≥ 3 4 \frac{1}{(1+x)^2}+\frac{1}{(1+y)^2}+\frac{1}{(1+z)^2}\ge \frac{3}{4} ( 1 + x ) 2 1 + ( 1 + y ) 2 1 + ( 1 + z ) 2 1 ≥ 4 3
问题初探
troy很快给出了两个数情况的一种初等证明 :a , b > 0 a,b\gt 0 a , b > 0 a + b = 4 a+b=4 a + b = 4 f = ( a + 1 a ) ( b + 1 b ) = a b + a 2 + b 2 + 1 a b f=(a+\frac 1a)(b+\frac 1b)=ab+\frac{a^2+b^2+1}{ab} f = ( a + a 1 ) ( b + b 1 ) = a b + a b a 2 + b 2 + 1 a 2 + b 2 + 2 a b = ( a + b ) 2 a^2+b^2+2ab=(a+b)^2 a 2 + b 2 + 2 a b = ( a + b ) 2 f = a b + ( a + b ) 2 − 2 a b + 1 a b = a b + 16 − 2 a b a b + 1 a b = a b + 17 a b − 2 f = ab+\frac{(a+b)^2-2ab+1}{ab}=ab+\frac{16-2ab}{ab}+\frac1{ab}=ab+\frac{17}{ab}-2 f = a b + a b ( a + b ) 2 − 2 a b + 1 = a b + a b 1 6 − 2 a b + a b 1 = a b + a b 1 7 − 2 a b = t ab=t a b = t f = t + 17 t − 2 f = t+\frac{17}t-2 f = t + t 1 7 − 2 a , b a,b a , b x 2 − 4 x + t = 0 x^2-4x+t=0 x 2 − 4 x + t = 0 Δ = 4 2 − 4 t ≥ 0 \Delta=4^2-4t\ge 0 Δ = 4 2 − 4 t ≥ 0 t ≤ 4 t\le 4 t ≤ 4 a b ≤ 4 ab\le 4 a b ≤ 4 y = x + 17 x y=x+\frac{17}x y = x + x 1 7 ( 0 , 17 ) (0,\sqrt{17}) ( 0 , 1 7 ) ( 0 , 4 ] (0,4] ( 0 , 4 ] y m i n = 4 + 17 4 ymin=4+\frac{17}4 y m i n = 4 + 4 1 7 f = t + 17 t − 2 ≥ 4 + 17 4 − 2 = 25 4 f=t+\frac{17}t-2\ge 4+\frac{17}4-2=\frac{25}4 f = t + t 1 7 − 2 ≥ 4 + 4 1 7 − 2 = 4 2 5
2天后,mathe说他给出的附件里面通过使用数学分析给出了3个数情况的证明,并且得出四个数和为8不再在四个数都相等时取到最小值了,可惜附件已经无法访问了。
wayne分析得出 a + b = T ≥ 2 2 + 5 = 4.116342054542985 a+b=T\ge 2 \sqrt{2 + \sqrt{5}}=4.116342054542985 a + b = T ≥ 2 2 + 5 = 4 . 1 1 6 3 4 2 0 5 4 5 4 2 9 8 5 ( 1 a + a ) ( b + 1 b ) (\frac1a + a)(b + \frac1b) ( a 1 + a ) ( b + b 1 ) a 4 + a 2 T 2 − 2 a 3 T − T 2 − 1 = 0 a^4 + a^2 T^2- 2 a^3 T - T^2 -1 = 0 a 4 + a 2 T 2 − 2 a 3 T − T 2 − 1 = 0 1 2 ( a + a 2 − 4 1 + a 2 ) \frac12 (a + \sqrt{a^2 - 4 \sqrt{1 + a^2}}) 2 1 ( a + a 2 − 4 1 + a 2 ) 2 T 2 + 1 − 2 2\sqrt{T^2 + 1} - 2 2 T 2 + 1 − 2 a = T 2 a=\frac T2 a = 2 T
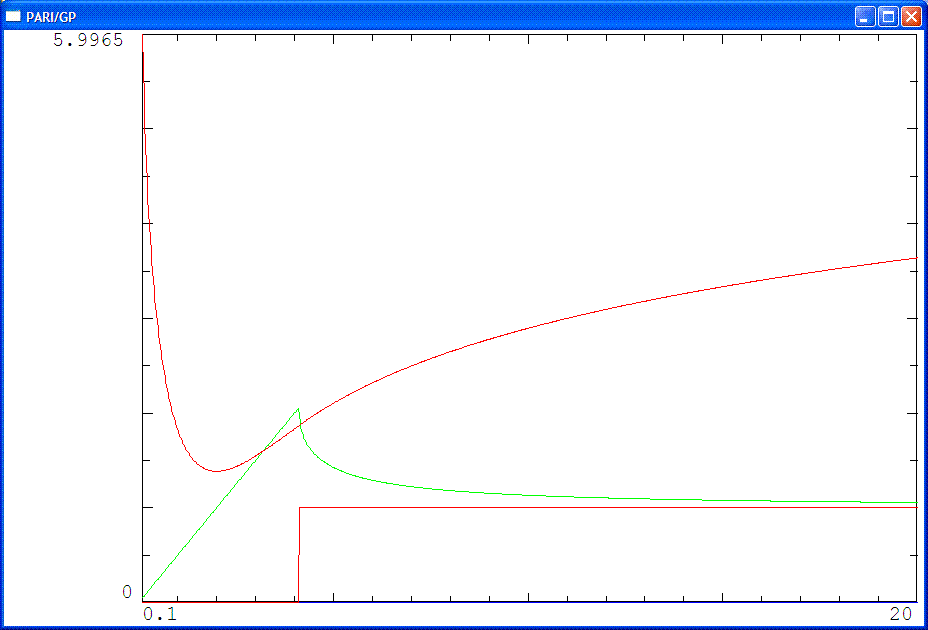
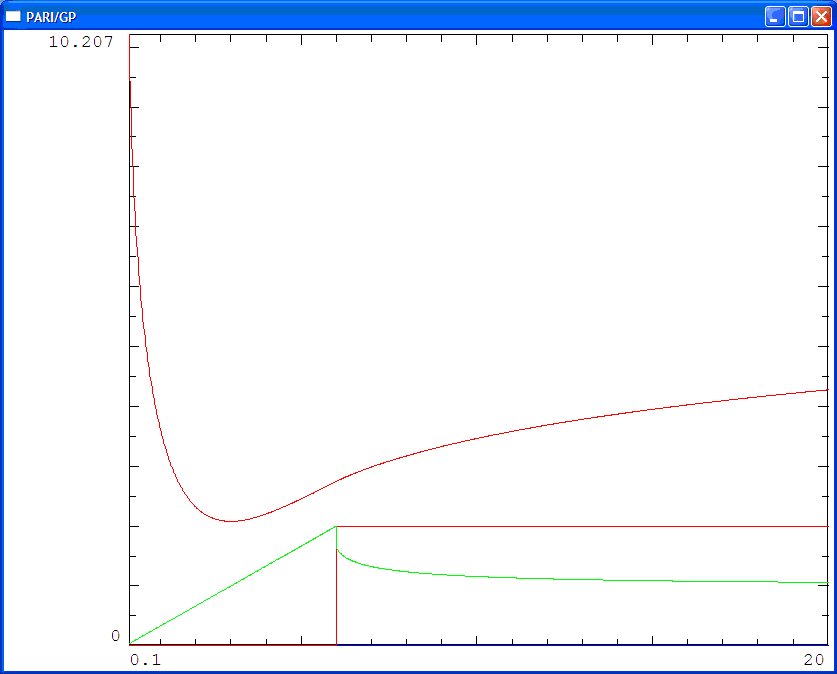
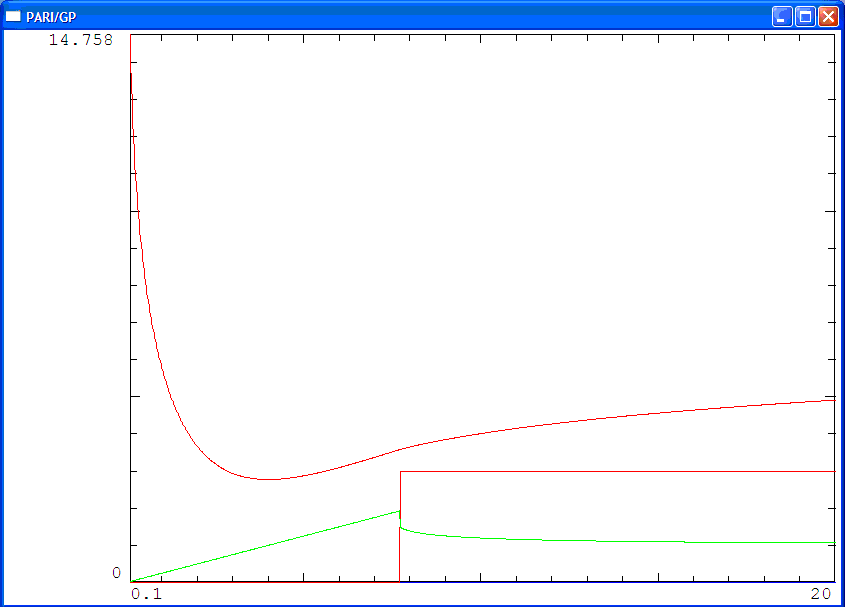
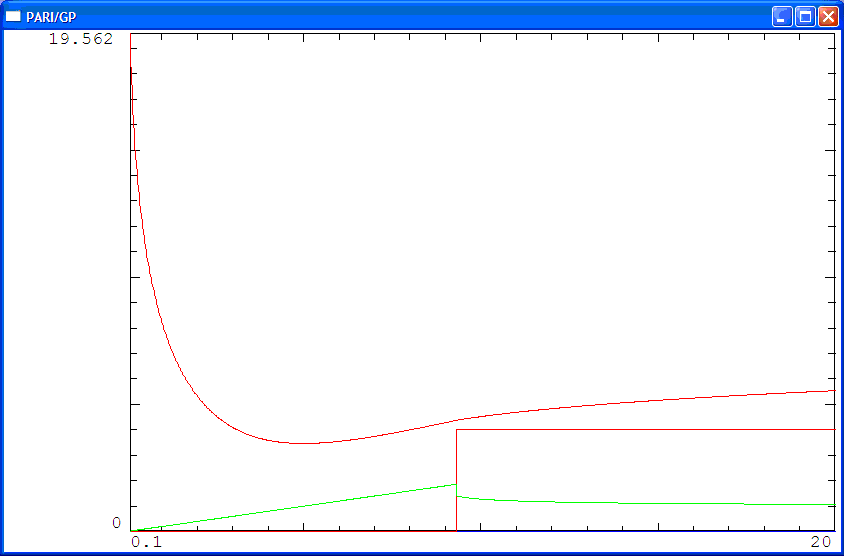
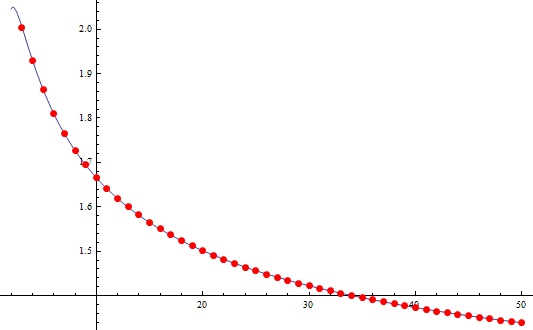
mathe试着用pari/gp做出不超过5个数时的最小值图像
从上面的图中可以看出,对于n比较大的情况,结论还是挺简单的:也就是n个数全相等或n-1个较小的数全相等时才取到最小值.n = k ≥ 3 n=k\ge 3 n = k ≥ 3 x 1 , x 2 , . . . , x k x_1,x_2,...,x_k x 1 , x 2 , . . . , x k x 1 = x 2 = . . . = x k = T k x_1=x_2=...=x_k=\frac Tk x 1 = x 2 = . . . = x k = k T x 1 = x 2 = . . . = x h , x h + 1 = . . . = x k , x 1 2 x k 2 = ( x 1 + x k ) 2 + 1 x_1=x_2=...=x_h,x_{h+1}=...=x_k,x_1^2x_k^2=(x_1+x_k)^2+1 x 1 = x 2 = . . . = x h , x h + 1 = . . . = x k , x 1 2 x k 2 = ( x 1 + x k ) 2 + 1 2 ≤ h ≤ k − 2 2\le h\le k-2 2 ≤ h ≤ k − 2 x 2 , x 3 , . . . , x h , x h + 1 , . . . , x k x_2,x_3,...,x_h,x_{h+1},...,x_k x 2 , x 3 , . . . , x h , x h + 1 , . . . , x k k − 1 k-1 k − 1 T − x 1 T-x_1 T − x 1 x 1 < x 2 = . . . = x h = . . . = x k − 1 x_1\lt x_2=...=x_h=...=x_{k-1} x 1 < x 2 = . . . = x h = . . . = x k − 1 k − 1 k-1 k − 1 T − x k T-x_k T − x k
但是上面证明从n = 2 n=2 n = 2 n = 3 n=3 n = 3 k ≥ 4 k\ge 4 k ≥ 4 k = 3 k=3 k = 3 x 1 < x 2 = x 3 x_1\lt x_2=x_3 x 1 < x 2 = x 3 ( x 1 , x 2 ) (x_1,x_2) ( x 1 , x 2 ) T − x 3 T-x_3 T − x 3 ( x 2 , x 2 ) (x_2,x_2) ( x 2 , x 2 ) T − x 1 T-x_1 T − x 1 T − x 3 < T − x 1 T-x_3\lt T-x_1 T − x 3 < T − x 1 T − x 3 T-x_3 T − x 3 T − x 1 T-x_1 T − x 1 2 2 + 5 2\sqrt{2+\sqrt{5}} 2 2 + 5 2 2 + 5 2\sqrt{2+\sqrt{5}} 2 2 + 5 n = 3 n=3 n = 3
现在还有余下几个问题:T ( n ) ≤ n n − 1 T ( n − 1 ) T(n)\le \frac{n}{n-1}T(n-1) T ( n ) ≤ n − 1 n T ( n − 1 )
凹凸函数不等式
icesheep提议使用一个控制不等式 x i x_i x i x i x_i x i x i x_i x i x i x_i x i x i x_i x i x y z = 1 xyz=1 x y z = 1 1 ( 1 + x ) 2 + 1 ( 1 + y ) 2 + 1 ( 1 + z ) 2 ≥ 3 4 \frac1{(1+x)^2}+\frac1{(1+y)^2}+\frac1{(1+z)^2}\ge \frac34 ( 1 + x ) 2 1 + ( 1 + y ) 2 1 + ( 1 + z ) 2 1 ≥ 4 3 x , y , z x,y,z x , y , z exp ( a ) , exp ( b ) , exp ( c ) \exp(a),\exp(b),\exp(c) exp ( a ) , exp ( b ) , exp ( c ) f ( a ) + f ( b ) + f ( c ) ≥ 3 4 f(a)+f(b)+f(c)\ge \frac34 f ( a ) + f ( b ) + f ( c ) ≥ 4 3 f ( x ) = 1 ( 1 + e x ) 2 f(x)=\frac1{(1+e^x)^2} f ( x ) = ( 1 + e x ) 2 1 f ′ ′ ( x ) = 4 e 2 x − 2 e x ( e x + 1 ) 2 f^{\prime\prime}(x)=\frac{4e^{2x}-2e^x}{(e^x+1)^2} f ′ ′ ( x ) = ( e x + 1 ) 2 4 e 2 x − 2 e x x = − ln ( 2 ) x=-\ln(2) x = − ln ( 2 ) a < − ln ( 2 ) , b = c > ln ( 2 ) a\lt-\ln(2),b=c\gt\ln(2) a < − ln ( 2 ) , b = c > ln ( 2 ) f ′ ( a ) = f ′ ( b ) f^{\prime}(a)=f^{\prime}(b) f ′ ( a ) = f ′ ( b ) a + b + c = 0 a+b+c=0 a + b + c = 0 a = − 2 b a=-2b a = − 2 b f ′ ( a ) = f ′ ( b ) f^{\prime}(a)=f^{\prime}(b) f ′ ( a ) = f ′ ( b ) 2 ( e b − 1 ) e b ( e 2 b + e b + 1 ) ( 3 e 2 b + 1 ) ( e b + 1 ) 3 ( e 2 b + 1 ) 3 = 0 \frac{2(e^b-1)e^b(e^{2b}+e^b+1)(3e^{2b}+1)}{(e^b+1)^3(e^{2b}+1)^3}=0 ( e b + 1 ) 3 ( e 2 b + 1 ) 3 2 ( e b − 1 ) e b ( e 2 b + e b + 1 ) ( 3 e 2 b + 1 ) = 0 b > ln ( 2 ) b\gt\ln(2) b > ln ( 2 ) b = 0.84359872296889 > ln ( 2 ) b=0.84359872296889\gt\ln(2) b = 0 . 8 4 3 5 9 8 7 2 2 9 6 8 8 9 > ln ( 2 ) a = b = c a=b=c a = b = c
进一步分析
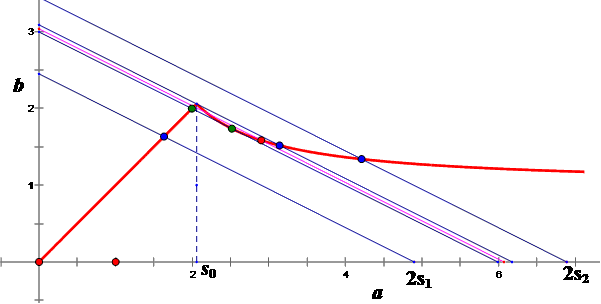
我们知道对于这个问题,hujunhua 定义了隐函数x 2 y 2 = ( x + y ) 2 + 1 x^2y^2=(x+y)^2+1 x 2 y 2 = ( x + y ) 2 + 1 ( x 1 , y 1 ) , ( x 2 , y 2 ) (x_1,y_1),(x_2,y_2) ( x 1 , y 1 ) , ( x 2 , y 2 ) x 1 2 y 1 2 = ( x 1 + y 1 ) 2 + 1 , x 2 2 y 2 2 = ( x 2 + y 2 ) 2 + 1 x_1^2y_1^2=(x_1+y_1)^2+1,x_2^2y_2^2=(x_2+y_2)^2+1 x 1 2 y 1 2 = ( x 1 + y 1 ) 2 + 1 , x 2 2 y 2 2 = ( x 2 + y 2 ) 2 + 1 ( x 1 + x 2 ) 2 ( y 1 + y 2 ) 2 16 ≥ ( x 1 + x 2 + y 1 + y 2 ) 2 4 + 1 \frac{(x_1+x_2)^2(y_1+y_2)^2}{16}\ge\frac{(x_1+x_2+y_1+y_2)^2}4+1 1 6 ( x 1 + x 2 ) 2 ( y 1 + y 2 ) 2 ≥ 4 ( x 1 + x 2 + y 1 + y 2 ) 2 + 1 a x 1 + b y 1 = a x 2 + b y 2 = c ax_1+by_1=ax_2+by_2=c a x 1 + b y 1 = a x 2 + b y 2 = c ( x 0 = x 1 + x 2 2 , y 0 = y 1 + y 2 2 ) (x_0=\frac{x_1+x_2}2,y_0=\frac{y_1+y_2}2) ( x 0 = 2 x 1 + x 2 , y 0 = 2 y 1 + y 2 ) a x 0 + b y 0 = c ax_0+by_0=c a x 0 + b y 0 = c x 2 y 2 x^2y^2 x 2 y 2 a x + b y = c ax+by=c a x + b y = c f ( x ) = ln ( x + 1 x ) , x > 0 f(x)=\ln(x+\frac1x),x\gt 0 f ( x ) = ln ( x + x 1 ) , x > 0 x + ( n − 1 ) y = n s x+(n-1)y=ns x + ( n − 1 ) y = n s f ( x ) + ( n − 1 ) f ( y ) f(x)+(n-1)f(y) f ( x ) + ( n − 1 ) f ( y ) g ( y ) = f ( n s − ( n − 1 ) y ) + ( n − 1 ) f ( y ) g(y)=f(ns-(n-1)y)+(n-1)f(y) g ( y ) = f ( n s − ( n − 1 ) y ) + ( n − 1 ) f ( y ) g ′ ( y ) = − ( n − 1 ) f ′ ( x ) + ( n − 1 ) f ′ ( y ) g^{\prime}(y)=-(n-1)f^{\prime}(x)+(n-1)f^{\prime}(y) g ′ ( y ) = − ( n − 1 ) f ′ ( x ) + ( n − 1 ) f ′ ( y ) f ′ ( y ) = f ′ ( x ) f^{\prime}(y)=f^{\prime}(x) f ′ ( y ) = f ′ ( x ) g ′ ( y ) = 0 g^{\prime}(y)=0 g ′ ( y ) = 0 g ′ ′ ( y ) = ( n − 1 ) 2 f ′ ′ ( x ) + ( n − 1 ) f ′ ′ ( y ) g^{\prime\prime}(y)=(n-1)^2f^{\prime\prime}(x)+(n-1)f^{\prime\prime}(y) g ′ ′ ( y ) = ( n − 1 ) 2 f ′ ′ ( x ) + ( n − 1 ) f ′ ′ ( y ) f ′ ( y ) = y 2 − 1 y 3 + y , f ′ ′ ( y ) = 1 + 4 y 2 − y 4 y 2 ( y 2 + 1 ) 2 f^{\prime}(y)=\frac{y^2-1}{y^3+y},f^{\prime\prime}(y)=\frac{1+4y^2-y^4}{y^2(y^2+1)^2} f ′ ( y ) = y 3 + y y 2 − 1 , f ′ ′ ( y ) = y 2 ( y 2 + 1 ) 2 1 + 4 y 2 − y 4
我们查看hujunhua定义的曲线x 2 y 2 = ( x + y ) 2 + 1 x^2y^2=(x+y)^2+1 x 2 y 2 = ( x + y ) 2 + 1 f ′ ( x ) = f ′ ( y ) f^{\prime}(x)=f^{\prime}(y) f ′ ( x ) = f ′ ( y ) d y d x = f ′ ′ ( x ) f ′ ′ ( y ) \frac{dy}{dx}=\frac{f^{\prime\prime}(x)}{f^{\prime\prime}(y)} d x d y = f ′ ′ ( y ) f ′ ′ ( x ) 27# 最后的要求相当于在曲线x 2 y 2 = ( x + y ) 2 + 1 x^2y^2=(x+y)^2+1 x 2 y 2 = ( x + y ) 2 + 1 − 1 n − 1 -\frac1{n-1} − n − 1 1 f ( x ) + ( n − 1 ) f ( y ) − n f ( s ) f(x)+(n-1)f(y)-nf(s) f ( x ) + ( n − 1 ) f ( y ) − n f ( s ) 24# 的图像。也就是说,我上面用二分法来计算总是不会出问题的,而我们讨论的s的分界点是唯一存在的。x 2 y 2 = ( x + y ) 2 + 1 x^2y^2=(x+y)^2+1 x 2 y 2 = ( x + y ) 2 + 1 x < y x\lt y x < y x > y x\gt y x > y x < s 0 = 2 + 5 x\lt s_0=\sqrt{2+\sqrt{5}} x < s 0 = 2 + 5 x = y x=y x = y
x + ( n − 1 ) y = n s x+(n-1)y=ns x + ( n − 1 ) y = n s ( a + 1 a ) ( b + 1 b ) ( c + 1 c ) (a+\frac1a)(b+\frac1b)(c+\frac1c) ( a + a 1 ) ( b + b 1 ) ( c + c 1 ) s 3 = 2.00286 s_3=2.00286 s 3 = 2 . 0 0 2 8 6 s 3 s_3 s 3 wayne计算出对于更大n的界限 :
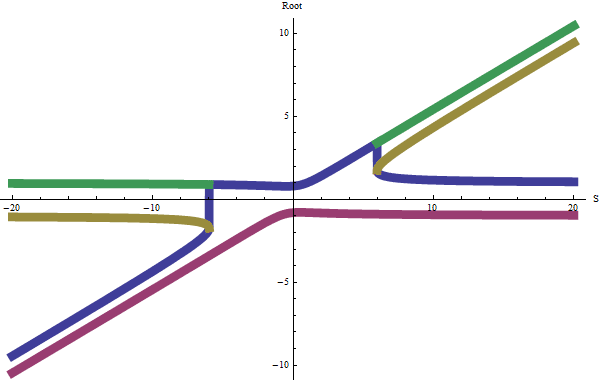
而问题最小值可以转化为求x 1 2 x n 2 = ( x 1 + x n ) 2 − 1 , ( n − 1 ) x 1 + x n = S x_1^2x_n^2=(x_1+x_n)^2-1,(n-1)x_1+x_n=S x 1 2 x n 2 = ( x 1 + x n ) 2 − 1 , ( n − 1 ) x 1 + x n = S 0 < x 1 < S n 0\lt x_1\lt \frac Sn 0 < x 1 < n S S n \frac Sn n S x n x_n x n x 1 x_1 x 1 f ( X ) = X 4 − 2 S X 3 + ( S 2 − n 2 + 4 n − 4 ) X 2 + ( 4 − 2 n ) S X − S 2 − n 2 + 2 n − 1 f(X)=X^4-2SX^3+(S^2-n^2+4n-4)X^2+(4-2n)SX-S^2-n^2+2n-1 f ( X ) = X 4 − 2 S X 3 + ( S 2 − n 2 + 4 n − 4 ) X 2 + ( 4 − 2 n ) S X − S 2 − n 2 + 2 n − 1 f ( 0 ) = − S 2 − ( n − 1 ) 2 < 0 f(0)=-S^2-(n-1)^2\lt 0 f ( 0 ) = − S 2 − ( n − 1 ) 2 < 0 f ( S n ) ( n − 1 ) 2 = ( S n ) 4 − 4 ( S n ) 2 − 1 \frac{f(\frac Sn)}{(n-1)^2}=(\frac Sn)^4-4(\frac Sn)^2-1 ( n − 1 ) 2 f ( n S ) = ( n S ) 4 − 4 ( n S ) 2 − 1 f c ( X ) = 4 X 3 − 6 S X 2 + 2 ( S 2 − n 2 + 4 n − 4 ) X + ( 4 − 2 n ) S fc(X)=4X^3-6SX^2+2(S^2-n^2+4n-4)X+(4-2n)S f c ( X ) = 4 X 3 − 6 S X 2 + 2 ( S 2 − n 2 + 4 n − 4 ) X + ( 4 − 2 n ) S f ′ ( 0 ) = ( 4 − 2 n ) S < 0 f^{\prime}(0)=(4-2n)S\lt 0 f ′ ( 0 ) = ( 4 − 2 n ) S < 0 f ′ ( S n ) n 3 ( n − 1 ) ( n − 2 ) = 2 S 3 − 4 n 2 S = 2 S ( S 2 − 2 n 2 ) f^{\prime}(\frac Sn)\frac{n^3}{(n-1)(n-2)}=2S^3-4n^2S=2S(S^2-2n^2) f ′ ( n S ) ( n − 1 ) ( n − 2 ) n 3 = 2 S 3 − 4 n 2 S = 2 S ( S 2 − 2 n 2 ) f ′ ′ ( X ) = 12 X 2 − 12 S X + 2 S 2 − 2 n 2 + 8 n − 8 f^{\prime\prime}(X)=12X^2-12SX+2S^2-2n^2+8n-8 f ′ ′ ( X ) = 1 2 X 2 − 1 2 S X + 2 S 2 − 2 n 2 + 8 n − 8 f ′ ′ ( 0 ) = 2 ( S 2 − ( n − 2 ) 2 ) f^{\prime\prime}(0)=2(S^2-(n-2)^2) f ′ ′ ( 0 ) = 2 ( S 2 − ( n − 2 ) 2 ) f ′ ′ ( S n ) = ( 2 n 2 − 12 n + 12 ) S 2 − 2 n 4 + 8 n 3 − 8 n 2 n 2 f^{\prime\prime}(\frac Sn)=\frac{(2n^2-12n+12)S^2-2n^4+8n^3-8n^2}{n^2} f ′ ′ ( n S ) = n 2 ( 2 n 2 − 1 2 n + 1 2 ) S 2 − 2 n 4 + 8 n 3 − 8 n 2 f ′ ′ ( X ) f^{\prime\prime}(X) f ′ ′ ( X ) ( 0 , S 2 ) (0,\frac S2) ( 0 , 2 S ) 0 < S < n − 2 0\lt S\lt n-2 0 < S < n − 2 f ′ ′ ( X ) < 0 , f ′ ( X ) f^{\prime\prime}(X)\lt 0,f^{\prime}(X) f ′ ′ ( X ) < 0 , f ′ ( X ) f ′ ( 0 ) < 0 f^{\prime}(0)\lt 0 f ′ ( 0 ) < 0 f ′ ( X ) < 0 f^{\prime}(X)\lt 0 f ′ ( X ) < 0 f ( X ) f(X) f ( X ) f ( 0 ) < 0 f(0)\lt 0 f ( 0 ) < 0 f ( X ) f(X) f ( X ) ( 0 , S n ) (0,\frac Sn) ( 0 , n S ) n − 2 ≤ S < n ( n − 2 ) n 2 − 6 n + 6 < 2 n n-2\le S\lt\frac{n(n-2)}{\sqrt{n^2-6n+6}}<\sqrt{2}n n − 2 ≤ S < n 2 − 6 n + 6 n ( n − 2 ) < 2 n f ′ ′ ( X ) = 0 f^{\prime\prime}(X)=0 f ′ ′ ( X ) = 0 f ′ ( X ) f^{\prime}(X) f ′ ( X ) f ′ ( 0 ) < 0 f^{\prime}(0)\lt 0 f ′ ( 0 ) < 0 f ′ ( S n ) < 0 f^{\prime}(\frac Sn)\lt 0 f ′ ( n S ) < 0 f ′ ′ ( X ) f^{\prime\prime}(X) f ′ ′ ( X ) 3 S 2 + 2 n 2 − 8 n + 8 ) + 3 S 6 \frac{\sqrt{3}\sqrt{S^2+2n^2-8n+8)+3S}}6 6 3 S 2 + 2 n 2 − 8 n + 8 ) + 3 S f ′ ( X ) f^{\prime}(X) f ′ ( X ) − S 2 + 2 n 2 − 8 n + 8 ( 3 S 2 + 2 3 n 2 − 8 3 n + 8 3 ) + ( 9 n 2 − 18 n ) S 9 < 0 -\frac{\sqrt{S^2+2n^2-8n+8}(\sqrt{3}S^2+2\sqrt{3}n^2-8\sqrt{3}n+8\sqrt{3})+(9n^2-18n)S}9\lt 0 − 9 S 2 + 2 n 2 − 8 n + 8 ( 3 S 2 + 2 3 n 2 − 8 3 n + 8 3 ) + ( 9 n 2 − 1 8 n ) S < 0 f ′ ( X ) < 0 f^{\prime}(X)\lt 0 f ′ ( X ) < 0 f ( X ) f(X) f ( X ) n ( n − 2 ) n 2 − 6 n + 6 ≤ S < 2 n \frac{n(n-2)}{\sqrt{n^2-6n+6}}\le S\lt\sqrt{2}n n 2 − 6 n + 6 n ( n − 2 ) ≤ S < 2 n f ′ ′ ( X ) ≥ 0 f^{\prime\prime}(X)\ge 0 f ′ ′ ( X ) ≥ 0 f ′ ( X ) f^{\prime}(X) f ′ ( X ) f ′ ( S n ) < 0 f^{\prime}(\frac Sn)\lt 0 f ′ ( n S ) < 0 f ′ ( X ) < 0 f^{\prime}(X)\lt 0 f ′ ( X ) < 0 f ( X ) f(X) f ( X ) S ≥ 2 n S\ge\sqrt{2}n S ≥ 2 n f ′ ′ ( X ) ≥ 0 f^{\prime\prime}(X)\ge 0 f ′ ′ ( X ) ≥ 0 f ′ ( X ) f^{\prime}(X) f ′ ( X ) f ′ ( 0 ) < 0 , f ′ ( S n ) ≥ 0 f^{\prime}(0)\lt 0,f^{\prime}(\frac Sn)\ge 0 f ′ ( 0 ) < 0 , f ′ ( n S ) ≥ 0 f ′ ( X ) = 0 f^{\prime}(X)=0 f ′ ( X ) = 0 f ( X ) f(X) f ( X ) 2 n ≤ S < 2 + 5 n \sqrt{2}n\le S\lt\sqrt{2+\sqrt{5}}n 2 n ≤ S < 2 + 5 n f ( 0 ) < 0 , f ( S n ) < 0 f(0)\lt 0,f(\frac Sn)\lt 0 f ( 0 ) < 0 , f ( n S ) < 0 S < 2 + 5 n S\lt \sqrt{2+\sqrt{5}}n S < 2 + 5 n f f f S ≥ 2 + 5 n S\ge \sqrt{2+\sqrt{5}}n S ≥ 2 + 5 n f ( X ) f(X) f ( X ) f ( 0 ) < 0 , f ( S n ) ≥ 0 f(0)\lt 0,f(\frac Sn)\ge 0 f ( 0 ) < 0 , f ( n S ) ≥ 0 f f f
所以我们可以得到S < 2 n S\lt\sqrt{2}n S < 2 n 2 n \sqrt{2}n 2 n 2 + 5 n \sqrt{2+\sqrt{5}}n 2 + 5 n f ( X ) f(X) f ( X ) f ( X ) = 4 ∗ X 4 − 4 ∗ S ∗ X 3 + ( S 2 − 1 ) ∗ X 2 + 2 ∗ S ∗ X − S 2 − 1 f(X)=4*X^4-4*S*X^3+(S^2-1)*X^2+2*S*X-S^2-1 f ( X ) = 4 ∗ X 4 − 4 ∗ S ∗ X 3 + ( S 2 − 1 ) ∗ X 2 + 2 ∗ S ∗ X − S 2 − 1
对于每个n有唯一的T n T_n T n T n T_n T n T n T_n T n x 1 2 x n 2 = ( x 1 + x n ) 2 + 1 x_1^2x_n^2=(x_1+x_n)^2+1 x 1 2 x n 2 = ( x 1 + x n ) 2 + 1 d x n d x 1 < − 1 \frac{dx_n}{dx_1}\lt -1 d x 1 d x n < − 1 x 1 < x n x_1\lt x_n x 1 < x n ( x 1 , x n ) (x_1,x_n) ( x 1 , x n ) ( T 2 , T 2 ) (\frac T2,\frac T2) ( 2 T , 2 T ) f ( x ) = ln ( x + 1 x ) f(x)=\ln(x+\frac1x) f ( x ) = ln ( x + x 1 ) ( x 1 , f ( x 1 ) ) , ( x n , f ( x n ) ) (x_1,f(x_1)),(x_n,f(x_n)) ( x 1 , f ( x 1 ) ) , ( x n , f ( x n ) ) x 1 x_1 x 1 x n x_n x n x ∗ x^{*} x ∗ f ( x 1 ) + f ( x n ) < 2 f ( x 1 + x n 2 ) f(x_1)+f(x_n)<2f(\frac{x_1+x_n}2) f ( x 1 ) + f ( x n ) < 2 f ( 2 x 1 + x n ) x 1 + x n 2 > x ∗ \frac{x_1+x_n}2\gt x^{*} 2 x 1 + x n > x ∗ x ∗ t x^{*t} x ∗ t x 1 x_1 x 1 x ∗ = ( 1 − λ ) x 1 + λ x n x^{*} =(1-\lambda)x_1+\lambda x_n x ∗ = ( 1 − λ ) x 1 + λ x n λ \lambda λ x 1 x_1 x 1 λ < 1 2 \lambda\lt \frac12 λ < 2 1 f ( ( 1 − λ ) x 1 + λ x n ) = ( 1 − λ ) f ( x 1 ) + λ f ( x n ) f((1-\lambda)x_1+\lambda x_n)=(1-\lambda)f(x_1)+\lambda f(x_n) f ( ( 1 − λ ) x 1 + λ x n ) = ( 1 − λ ) f ( x 1 ) + λ f ( x n ) x 1 x_1 x 1 f ′ ( x ∗ ) ( ( x n − x 1 ) d λ d x 1 + 1 − λ + λ d x n d x 1 ) = ( f ( x n ) − f ( x 1 ) ) d λ d x 1 + ( 1 − λ ) f ′ ( x 1 ) + λ f ′ ( x n ) d x n d x 1 f^{\prime}(x^{*})((x_n-x_1)\frac{d\lambda}{dx_1}+1-\lambda+\lambda\frac{dx_n}{dx_1})=(f(x_n)-f(x_1))\frac{d\lambda}{dx_1}+(1-\lambda)f^{\prime}(x_1)+\lambda f^{\prime}(x_n)\frac{dx_n}{dx_1} f ′ ( x ∗ ) ( ( x n − x 1 ) d x 1 d λ + 1 − λ + λ d x 1 d x n ) = ( f ( x n ) − f ( x 1 ) ) d x 1 d λ + ( 1 − λ ) f ′ ( x 1 ) + λ f ′ ( x n ) d x 1 d x n f ′ ( x 1 ) = f ′ ( x n ) f^{\prime}(x_1)=f^{\prime}(x_n) f ′ ( x 1 ) = f ′ ( x n ) d λ d x 1 = ( 1 − λ + λ d x n d x 1 ) ( f ′ ( x ∗ ) − f ′ ( x 1 ) ) f ( x n ) − f ( x 1 ) − f ′ ( x ∗ ) ( x n − x 1 ) \frac{d\lambda}{dx_1}=\frac{(1-\lambda+\lambda\frac{dx_n}{dx_1})(f^{\prime}(x^{*})-f^{\prime}(x_1))}{f(x_n)-f(x_1)-f^{\prime}(x^{*})(x_n-x_1)} d x 1 d λ = f ( x n ) − f ( x 1 ) − f ′ ( x ∗ ) ( x n − x 1 ) ( 1 − λ + λ d x 1 d x n ) ( f ′ ( x ∗ ) − f ′ ( x 1 ) ) f ′ ( x ∗ ) − f ′ ( x 1 ) f^{\prime}(x^{*})-f^{\prime}(x_1) f ′ ( x ∗ ) − f ′ ( x 1 ) d λ d x 1 \frac{d\lambda}{dx_1} d x 1 d λ ( 1 − λ + λ d x n d x 1 ) (1-\lambda+\lambda\frac{dx_n}{dx_1}) ( 1 − λ + λ d x 1 d x n ) d λ d x 1 < 0 \frac{d\lambda}{dx_1}\lt 0 d x 1 d λ < 0
添加λ \lambda λ x 1 x_1 x 1 ( 1 − λ + λ d x n d x 1 ) (1-\lambda+\lambda\frac{dx_n}{dx_1}) ( 1 − λ + λ d x 1 d x n )
对于n个数,我们已经知道取最小值必然两种情况之一:x 1 x_1 x 1 x n x_n x n ( x 1 x n ) 2 = ( x 1 + x n ) 2 + 1 (x_1x_n)^2=(x_1+x_n)^2+1 ( x 1 x n ) 2 = ( x 1 + x n ) 2 + 1 r = 1 n r=\frac 1n r = n 1 ( n − 1 ) f ( x 1 ) + f ( x n ) = n ( ( 1 − r ) f ( x 1 ) + r f ( x n ) (n-1)f(x_1)+f(x_n)=n((1-r)f(x_1)+rf(x_n) ( n − 1 ) f ( x 1 ) + f ( x n ) = n ( ( 1 − r ) f ( x 1 ) + r f ( x n ) n f ( ( 1 − r ) x 1 + r x n ) nf((1-r)x_1+rx_n) n f ( ( 1 − r ) x 1 + r x n ) n ( ( 1 − r ) f ( x 1 ) + r f ( x n ) − f ( ( 1 − r ) x 1 + r x n ) ) n((1-r)f(x_1)+rf(x_n)-f((1-r)x_1+rx_n)) n ( ( 1 − r ) f ( x 1 ) + r f ( x n ) − f ( ( 1 − r ) x 1 + r x n ) ) x 1 x_1 x 1 n ( ( 1 − r ) f ′ ( x 1 ) + r f ′ ( x n ) d x n d x 1 − f ′ ( ( 1 − r ) x 1 + r x n ) ( ( 1 − r ) + r d x n d x 1 ) ) = n ( 1 − r + r d x n d x 1 ) ( f ′ ( x 1 ) − f ′ ( ( 1 − r ) x 1 + r x n ) ) n((1-r)f^{\prime}(x_1)+rf^{\prime}(x_n)\frac{dx_n}{dx_1}-f^{\prime}((1-r)x_1+rx_n)((1-r)+r\frac{dx_n}{dx_1}))=n(1-r+r\frac{dx_n}{dx_1})(f^{\prime}(x_1)-f^{\prime}((1-r)x_1+rx_n)) n ( ( 1 − r ) f ′ ( x 1 ) + r f ′ ( x n ) d x 1 d x n − f ′ ( ( 1 − r ) x 1 + r x n ) ( ( 1 − r ) + r d x 1 d x n ) ) = n ( 1 − r + r d x 1 d x n ) ( f ′ ( x 1 ) − f ′ ( ( 1 − r ) x 1 + r x n ) )
记函数f ( x ) = ln ( x + 1 x ) f(x)=\ln(x+\frac{1}{x}) f ( x ) = ln ( x + x 1 ) x 1 , x 2 , … , x n x_1,x_2,\dots,x_n x 1 , x 2 , … , x n x 1 + x 2 + ⋯ + x n = S x_1+x_2+\dots+x_n=S x 1 + x 2 + ⋯ + x n = S T = f ( x 1 ) + f ( x 2 ) + ⋯ + f ( x n ) T=f(x_1)+f(x_2)+\dots+f(x_n) T = f ( x 1 ) + f ( x 2 ) + ⋯ + f ( x n ) f ′ ( x ) = x 2 − 1 x ( 1 + x 2 ) f^{\prime}(x)=\frac{x^2-1}{x(1+x^2)} f ′ ( x ) = x ( 1 + x 2 ) x 2 − 1 f ′ ′ ( x ) = 1 + 4 x 2 − x 4 x 2 ( 1 + x 2 ) 2 f^{\prime\prime}(x)=\frac{1+4x^2-x^4}{x^2(1+x^2)^2} f ′ ′ ( x ) = x 2 ( 1 + x 2 ) 2 1 + 4 x 2 − x 4 x > 0 x\gt 0 x > 0 f ′ ′ ( x ) = 0 f^{\prime\prime}(x)=0 f ′ ′ ( x ) = 0 x = x 0 = 2 + 5 = 2.058 … x=x_0=\sqrt{2+\sqrt{5}}=2.058\dots x = x 0 = 2 + 5 = 2 . 0 5 8 … x ≤ x 0 x\le x_0 x ≤ x 0 f ′ ( x ) f^{\prime}(x) f ′ ( x ) f ( x ) f(x) f ( x ) x ≥ x 0 x\ge x_0 x ≥ x 0 f ′ ( x ) f^{\prime}(x) f ′ ( x ) f ( x ) f(x) f ( x ) f ′ ( x ) f^{\prime}(x) f ′ ( x )
首先显然,边界条件对应某个x i → 0 x_i\to 0 x i → 0 f ′ ( x 1 ) = f ′ ( x 2 ) = ⋯ = f ′ ( x n ) f^{\prime}(x_1)=f^{\prime}(x_2)=\dots=f^{\prime}(x_n) f ′ ( x 1 ) = f ′ ( x 2 ) = ⋯ = f ′ ( x n ) f ′ ( x ) f^{\prime}(x) f ′ ( x ) x 1 , x 2 , … , x n x_1,x_2,\dots,x_n x 1 , x 2 , … , x n x 1 ≠ x n x_1\ne x_n x 1 = x n f ′ ( x 1 ) = f ′ ( x n ) f^{\prime}(x_1)=f^{\prime}(x_n) f ′ ( x 1 ) = f ′ ( x n ) x 1 2 x n 2 = ( x 1 + x n ) 2 + 1 x_1^2x_n^2=(x_1+x_n)^2+1 x 1 2 x n 2 = ( x 1 + x n ) 2 + 1 1 < x 1 < x 0 < x n 1\lt x_1\lt x_0\lt x_n 1 < x 1 < x 0 < x n x n x_n x n x n x_n x n x n − t , x n + t x_n-t,x_n+t x n − t , x n + t x n x_n x n x 1 x_1 x 1 x n x_n x n x n x_n x n x n = x 1 + x 1 4 + x 1 2 − 1 x 1 2 − 1 x_n=\frac{x_1+\sqrt{x_1^4+x_1^2-1}}{x_1^2-1} x n = x 1 2 − 1 x 1 + x 1 4 + x 1 2 − 1 x n x_n x n x 1 x_1 x 1
Δ n ( x 1 ) = n ( ( 1 − r ) f ( x 1 ) + r f ( x n ) − f ( ( 1 − r ) x 1 + r x n ) ) \Delta_n(x_1)=n((1-r)f(x_1)+rf(x_n)-f((1-r)x_1+rx_n)) Δ n ( x 1 ) = n ( ( 1 − r ) f ( x 1 ) + r f ( x n ) − f ( ( 1 − r ) x 1 + r x n ) ) r = 1 n r=\frac{1}{n} r = n 1 x 1 x_1 x 1 Δ n ′ ( x 1 ) = n ( ( 1 − r ) f ′ ( x 1 ) + r f ′ ( x n ) d x n d x 1 − f ′ ( ( 1 − r ) x 1 + r x n ) ( ( 1 − r ) + r d x n d x 1 ) ) = n ( 1 − r + r d x n d x 1 ) ( f ′ ( x 1 ) − f ′ ( ( 1 − r ) x 1 + r x n ) ) \Delta^{\prime}_n(x_1) = n((1-r)f^{\prime}(x_1)+rf^{\prime}(x_n)\frac{dx_n}{dx_1}-f^{\prime}((1-r)x_1+rx_n)((1-r)+r\frac{dx_n}{dx_1}))=n(1-r+r\frac{dx_n}{dx_1})(f^{\prime}(x_1)-f^{\prime}((1-r)x_1+rx_n)) Δ n ′ ( x 1 ) = n ( ( 1 − r ) f ′ ( x 1 ) + r f ′ ( x n ) d x 1 d x n − f ′ ( ( 1 − r ) x 1 + r x n ) ( ( 1 − r ) + r d x 1 d x n ) ) = n ( 1 − r + r d x 1 d x n ) ( f ′ ( x 1 ) − f ′ ( ( 1 − r ) x 1 + r x n ) ) f ′ ( x ) f^{\prime}(x) f ′ ( x ) f ′ ( ( 1 − r ) x 1 + r x n ) > f ′ ( x 1 ) = f ′ ( x n ) f^{\prime}((1-r)x_1+rx_n)\gt f^{\prime}(x_1)=f^{\prime}(x_n) f ′ ( ( 1 − r ) x 1 + r x n ) > f ′ ( x 1 ) = f ′ ( x n ) d x n d x 1 = − x 1 x n 2 − x 1 − x n x 1 2 x n − x 1 − x n = − x n x 1 x 1 2 x n 2 − x 1 2 − x 1 x n x 1 2 x n 2 − x 1 x n − x n 2 = − x n x 1 x n 2 + x 1 x n + 1 x 1 2 + x 1 x n + 1 \frac{dx_n}{dx_1}=-\frac{x_1x_n^2-x_1-x_n}{x_1^2x_n-x_1-x_n}=-\frac{x_n}{x_1}\frac{x_1^2x_n^2-x_1^2-x_1x_n}{x_1^2x_n^2-x_1x_n-x_n^2}=-\frac{x_n}{x_1}\frac{x_n^2+x_1x_n+1}{x_1^2+x_1x_n+1} d x 1 d x n = − x 1 2 x n − x 1 − x n x 1 x n 2 − x 1 − x n = − x 1 x n x 1 2 x n 2 − x 1 x n − x n 2 x 1 2 x n 2 − x 1 2 − x 1 x n = − x 1 x n x 1 2 + x 1 x n + 1 x n 2 + x 1 x n + 1 d x n d x 1 < 0 \frac{dx_n}{dx_1}\lt 0 d x 1 d x n < 0 x n x_n x n x 1 x_1 x 1 x n ≥ x 1 x_n\ge x_1 x n ≥ x 1 d x n d x 1 \frac{dx_n}{dx_1} d x 1 d x n x 1 x_1 x 1 d x n d x 1 \frac{dx_n}{dx_1} d x 1 d x n x 1 x_1 x 1
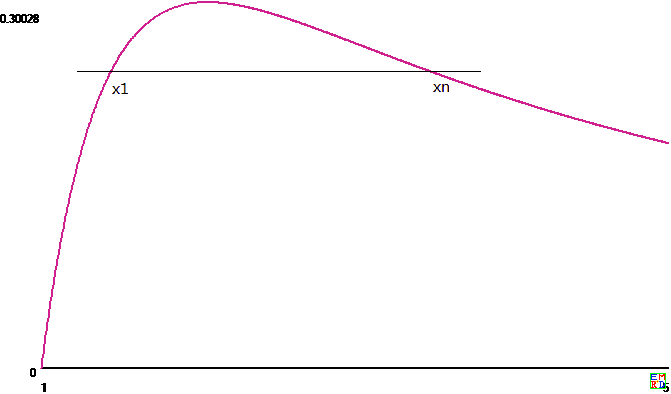
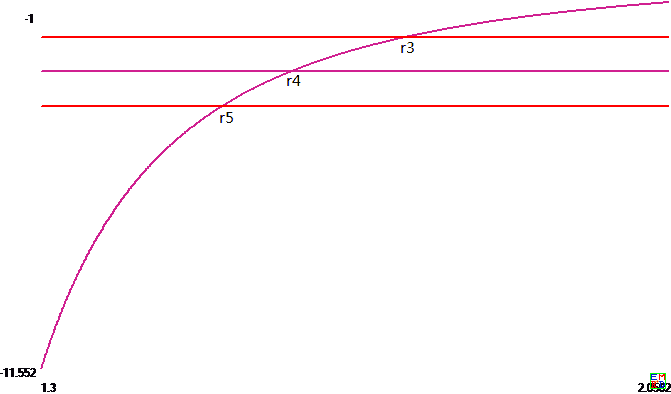
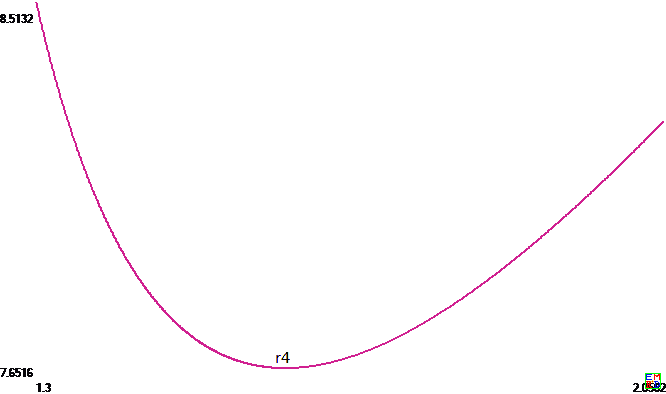
x 1 → 1 x_1\to 1 x 1 → 1 d x n d x 1 → − ∞ \frac{dx_n}{dx_1}\to -\infty d x 1 d x n → − ∞ x 1 → x 0 x_1\to x_0 x 1 → x 0 d x n d x 1 → − 1 \frac{dx_n}{dx_1}\to -1 d x 1 d x n → − 1 r n r_n r n x 1 = r n x_1=r_n x 1 = r n d x n d x 1 = − ( n − 1 ) \frac{dx_n}{dx_1}=-(n-1) d x 1 d x n = − ( n − 1 ) n ≥ 3 n\ge 3 n ≥ 3 Δ 4 ( x ) \Delta_4(x) Δ 4 ( x )
Δ n ( x 1 ) \Delta_n(x_1) Δ n ( x 1 ) x 1 < r n x_1\lt r_n x 1 < r n r n < x 1 ≤ x 0 r_n\lt x_1\le x_0 r n < x 1 ≤ x 0 Δ n ( x 0 ) = 0 , Δ n ( 1 ) = − ∞ \Delta_n(x_0)=0,\Delta_n(1)=-\infty Δ n ( x 0 ) = 0 , Δ n ( 1 ) = − ∞ s n s_n s n 1 < s n < r n 1\lt s_n\lt r_n 1 < s n < r n Δ n ( s n ) = 0 \Delta_n(s_n)=0 Δ n ( s n ) = 0 x 1 < s n x_1\lt s_n x 1 < s n Δ n ( x 1 ) < 0 \Delta_n(x_1)\lt 0 Δ n ( x 1 ) < 0 x 1 > s n x_1\gt s_n x 1 > s n Δ n ( x n ) > 0 \Delta_n(x_n)\gt 0 Δ n ( x n ) > 0 x 1 x_1 x 1 S = ( n − 1 ) x 1 + x n S=(n-1)x_1+x_n S = ( n − 1 ) x 1 + x n x 1 x_1 x 1 d S d x 1 = ( n − 1 ) + d x n d x 1 \frac{dS}{dx_1}=(n-1)+\frac{dx_n}{dx_1} d x 1 d S = ( n − 1 ) + d x 1 d x n x 1 < s n < r n x_1\lt s_n\lt r_n x 1 < s n < r n d S d x 1 < 0 \frac{dS}{dx_1}\lt 0 d x 1 d S < 0 x 1 x_1 x 1
x 1 = s n x_1=s_n x 1 = s n S = S n S=S_n S = S n x 1 < s n x_1\lt s_n x 1 < s n S > S n S\gt S_n S > S n S n S_n S n x i x_i x i S ≤ S n S\le S_n S ≤ S n x 1 x_1 x 1 r n r_n r n r n r_n r n s n s_n s n x 1 x_1 x 1 s n s_n s n r 3 = 1.740411449278029845734308926 , s 3 = 1.657192792516150065878529915 , S 3 = 6.008602224190500538235955480 r_3=1.740411449278029845734308926,s_3=1.657192792516150065878529915,S_3=6.008602224190500538235955480 r 3 = 1 . 7 4 0 4 1 1 4 4 9 2 7 8 0 2 9 8 4 5 7 3 4 3 0 8 9 2 6 , s 3 = 1 . 6 5 7 1 9 2 7 9 2 5 1 6 1 5 0 0 6 5 8 7 8 5 2 9 9 1 5 , S 3 = 6 . 0 0 8 6 0 2 2 2 4 1 9 0 5 0 0 5 3 8 2 3 5 9 5 5 4 8 0 r 4 = 1.600485180440240838317819642 , s 4 = 1.497336479006372785981767326 , S 4 = 7.713435665899921713440339745 r_4=1.600485180440240838317819642,s_4=1.497336479006372785981767326,S_4=7.713435665899921713440339745 r 4 = 1 . 6 0 0 4 8 5 1 8 0 4 4 0 2 4 0 8 3 8 3 1 7 8 1 9 6 4 2 , s 4 = 1 . 4 9 7 3 3 6 4 7 9 0 0 6 3 7 2 7 8 5 9 8 1 7 6 7 3 2 6 , S 4 = 7 . 7 1 3 4 3 5 6 6 5 8 9 9 9 2 1 7 1 3 4 4 0 3 3 9 7 4 5 r 5 = 1.517582550159295840149998641 , s 5 = 1.408470004464252711744740637 , S 5 = 9.320038250002624253886775023 r_5=1.517582550159295840149998641,s_5=1.408470004464252711744740637,S_5=9.320038250002624253886775023 r 5 = 1 . 5 1 7 5 8 2 5 5 0 1 5 9 2 9 5 8 4 0 1 4 9 9 9 8 6 4 1 , s 5 = 1 . 4 0 8 4 7 0 0 0 4 4 6 4 2 5 2 7 1 1 7 4 4 7 4 0 6 3 7 , S 5 = 9 . 3 2 0 0 3 8 2 5 0 0 0 2 6 2 4 2 5 3 8 8 6 7 7 5 0 2 3 r 6 = 1.461303403894868433140713446 , s 6 = 1.350919585834549644761334220 , S 6 = 10.86308628736897900157668245 r_6=1.461303403894868433140713446,s_6=1.350919585834549644761334220,S_6=10.86308628736897900157668245 r 6 = 1 . 4 6 1 3 0 3 4 0 3 8 9 4 8 6 8 4 3 3 1 4 0 7 1 3 4 4 6 , s 6 = 1 . 3 5 0 9 1 9 5 8 5 8 3 4 5 4 9 6 4 4 7 6 1 3 3 4 2 2 0 , S 6 = 1 0 . 8 6 3 0 8 6 2 8 7 3 6 8 9 7 9 0 0 1 5 7 6 6 8 2 4 5 r 100 = 1.100918455622057296344282356 , s 100 = 1.051229206129076187764123092 , S 100 = 125.0349255508031551479807498 r_{100}=1.100918455622057296344282356,s_{100}=1.051229206129076187764123092,S_{100}=125.0349255508031551479807498 r 1 0 0 = 1 . 1 0 0 9 1 8 4 5 5 6 2 2 0 5 7 2 9 6 3 4 4 2 8 2 3 5 6 , s 1 0 0 = 1 . 0 5 1 2 2 9 2 0 6 1 2 9 0 7 6 1 8 7 7 6 4 1 2 3 0 9 2 , S 1 0 0 = 1 2 5 . 0 3 4 9 2 5 5 5 0 8 0 3 1 5 5 1 4 7 9 8 0 7 4 9 8 r n ≈ 1 + 1 n − 1 r_n \approx1+\frac1{\sqrt{n-1}} r n ≈ 1 + n − 1 1 s n < r n s_n\lt r_n s n < r n S n S_n S n n − 1 + 2 n − 1 n-1+2\sqrt{n-1} n − 1 + 2 n − 1