四柱汉诺塔升级版

Sat, 25th January 2020Edit on Github汉诺塔算法

问题提出

KeyTo9_Fans于2008年2月在百度数学吧发布了四柱汉诺塔升级版问题:
有四个排成一行的柱子和n个大小不同的盘子，每次可以将一个盘子移动到相邻的柱子上，但是大盘子不能放在小盘子上面。请用最小的步数将n个盘子从第一个柱子全部移到第4个盘子。
热衷于进口Fans优秀题材的mathe在6月将题目进口到了数学研发论坛。
并提议:
这个问题在n不大（比如不超过10）时用计算机应该不难，但是n大一些就很难了。
看谁能够计算到最大的n.
还有对于比较大的n,比如n=20和n=30,计算最优的移动方案很难，所以我们还可以比赛对于n=20和n=30，看谁可以用最小的步数完成移动过程

初步进展

无心人计算出
n = 3 19步
n = 4 34步
如果分别是字母A、B、C、c、b、a代表移动 $1\to2, 2\to 3, 3\to 4, 4\to 3, 3\to 2, 2\to1$ 无心人给出移动的方案分别为:
3的
ABACBcAbaCBcbCBCABC 19步
4的
ABACBAbaBABAbcabaCBcbCBCABAbaBCABC 34步.

这个结果和KeyTo9_Fans的结果一致，他在4月就已经在数学吧给出了更多的结果:

n	f(n)
0	0
1	3
2	10
3	19
4	34
5	57
6	88
7	123
8	176
9	253
10	342
11	449
12	572
13	749

据说mathe随后写了一个C++代码，检验了KeyTo9_Fans的结果已经是最优的了, 只是可惜代码已经无法下载了。但是mathe表示由于空间复杂度的原因，我们很难再找出n更大的最优结果了。

Fans进入数学研发论坛

2009年11月，KeyTo9_Fans步入数学研发论坛发表他的意见：
做广度优先搜索时，扩展出来的新状态放在队列尾端。
而已经扩展过的状态是没有必要保留的，可以直接从队列头部清除，释放空间。
但为了防止走回头路，需要保留上一步扩展到的状态。
综上所述，扩展过程只需用三个数组：last[]，now[]，next[]。
逐一扫描now[]数组所记录的状态，把扩展出来的状态与last[]、now[]、next[]中的状态均比较一遍，如果是新的状态，则记录到next[]里。
扫描完毕后，把数组滚动一下，即 last = now，now = next，然后继续扫描now[]数组。
对n=16做这种推进式的扩展，高峰时每个数组存储的状态数为一千多万（为了方便查找重复状态，当然是以状态的哈希值作为下标），共占用200M左右的内存，还不至于动用硬盘空间。
这种推进式的扩展没有保留扩展路径，所以只能得到最佳步数，不能得到方案。
所幸的是，n<=16的情况都通过手工操作找到了最佳步数对应的一种可行方案。
Fans还提供了对应的游戏以供下载.

极限拓展

KeyTo9_Fans继续努力为更大的n搜索较优秀的结果:
当16<n<29时，捆绑前(n-13)个盘子，即把最小的几个盘子作为一个整体。
这个整体直接在1柱和4柱上移动，移动1次的代价为f(k)，k为这个整体的盘子数，f是前面已经算好的数据。
例如，n=17时，捆绑1~4盘，作为一个整体，移动代价为f(4)=34。
这样就相当于只有14个盘子了，状态数为4^14，是可以全部存下来的。
由于捆绑了4个盘子，而f(5)、f(6)、……的移动无法仅用f(4)来表示，所以移动规则要相应地修改。
除了把一个盘子移到相邻的柱子之外，还要考虑1次性把多个盘子从1柱移到4柱或移回来。
即f(4)到f(16)的移动均可直接进行。
这样，问题就变成了在含有4^14个顶点、标有长度的边的无向图中找最短路径。
由于这个图的边是有规律且很稀疏的，所以即使顶点数高达4^14，找最短路径也不成问题。
如果捆绑前(n-13)个盘子不会造成结果不优，那么1盘到28盘的移动步数分别为：

当n>28时，捆绑前(n-13)个盘子会造成结果不优，于是停止寻找最短路径，手工往下推导。
仿照前28个盘子的移动方案，以相同的方式移动29盘至32盘，结果为：

Fans还将移动模式制作成图片:
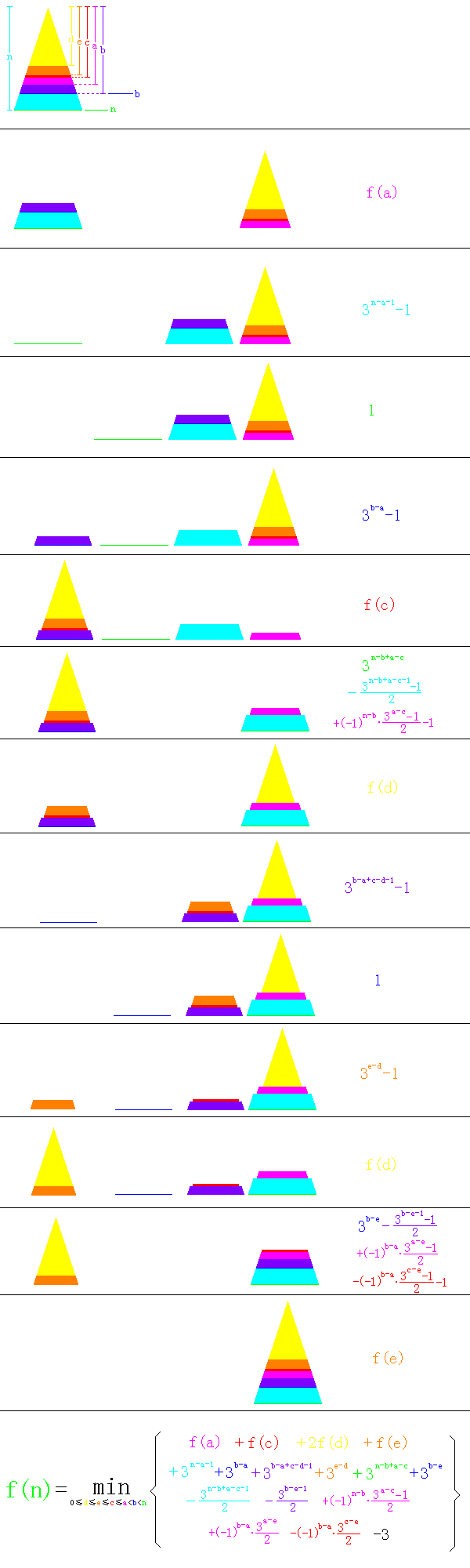
hanoi4
但n=0、n=1、n=3和n=6例外，需要特殊处理。
令f(0)=0，f(1)=3，f(3)=19，f(6)=88，
然后利用f(0)到f(n)的结果，枚举a,b,c,d,e的值，就可以求得f(n+1)。
这样求f(n)的时间复杂度为O(n^6)。
f(2)到f(100)的结果如下：

  n      f(n)     d  e  c  a  b
--------------------------------
  2:       10     0  0  0  0  1
  3:       19     0  0  0  0  1
  4:       34     0  0  1  1  2
  5:       57     1  1  2  2  3
  6:       88     1  1  2  2  3
  7:      123     1  2  3  3  4
  8:      176     2  3  4  4  5
  9:      253     3  3  5  5  6
 10:      342     3  4  5  6  7
 11:      449     3  4  6  6  7
 12:      572     4  5  7  7  8
 13:      749     5  7  7  8 10
 14:      980     5  7  8  9 11
 15:     1261     6  8  9 10 12
 16:     1560     6  8  9 10 12
 17:     1903     7  9 10 11 13
 18:     2328     8 10 11 12 14
 19:     2889     9 11 12 13 15
 20:     3562    10 12 12 14 17
 21:     4377    10 13 13 15 18
 22:     5276    10 13 13 15 18
 23:     6251    11 14 14 16 19
 24:     7392    12 14 16 17 19
 25:     8779    13 16 16 18 21
 26:    10488    14 17 17 19 22
 27:    12469    14 17 18 20 23
 28:    14832    15 18 19 21 24
 29:    17497    15 18 19 21 24
 30:    20228    16 19 20 22 25
 31:    23377    17 20 21 23 26
 32:    27082    18 21 22 24 27
 33:    31465    19 22 23 25 28
 34:    36636    20 23 24 26 29
 35:    42581    20 24 24 27 31
 36:    49348    21 25 25 28 32
 37:    57157    22 25 26 28 32
 38:    65222    22 26 26 29 33
 39:    73865    23 27 27 30 34
 40:    84022    24 28 28 31 35
 41:    95757    25 28 30 32 35
 42:   109094    26 30 30 33 37
 43:   124525    27 31 31 34 38
 44:   142220    27 31 32 35 39
 45:   161801    28 32 33 36 40
 46:   184494    29 33 34 37 41
 47:   208359    30 34 34 37 42
 48:   233220    30 34 35 38 42
 49:   260873    31 35 36 39 43
 50:   293016    32 36 37 40 44
 51:   329391    33 37 38 41 45
 52:   369778    34 38 39 42 46
 53:   415899    35 39 40 43 47
 54:   468000    35 40 40 44 49
 55:   524585    36 41 41 45 50
 56:   589570    37 42 42 46 51
 57:   660389    38 42 43 46 51
 58:   732678    38 43 43 47 52
 59:   810215    39 44 44 48 53
 60:   897344    40 45 45 49 54
 61:   998343    41 46 46 50 55
 62:  1109122    42 47 47 51 56
 63:  1230093    43 48 48 52 57
 64:  1366910    44 49 49 53 58
 65:  1522459    45 50 50 54 59
 66:  1687510    45 50 51 55 60
 67:  1874643    46 51 52 56 61
 68:  2079700    47 52 53 57 62
 69:  2294287    48 53 53 57 63
 70:  2516366    48 53 54 58 63
 71:  2757895    49 54 55 59 64
 72:  3030880    50 55 56 60 65
 73:  3340433    51 56 57 61 66
 74:  3675094    52 57 58 62 67
 75:  4038133    53 58 59 63 68
 76:  4443818    54 59 60 64 69
 77:  4898969    55 60 60 65 71
 78:  5384602    55 61 61 66 72
 79:  5923263    56 62 62 67 73
 80:  6511900    57 63 63 68 74
 81:  7144699    58 64 64 69 75
 82:  7793996    58 64 64 69 75
 83:  8482247    59 65 65 70 76
 84:  9228136    60 66 66 71 77
 85: 10077385    61 67 67 72 78
 86: 11018610    62 68 68 73 79
 87: 12024387    63 69 69 74 80
 88: 13105218    64 70 70 75 81
 89: 14305059    65 71 71 76 82
 90: 15636282    66 72 72 77 83
 91: 17081249    66 72 73 78 84
 92: 18638390    67 73 74 79 85
 93: 20334841    68 74 75 80 86
 94: 22165538    69 75 76 81 87
 95: 24079237    70 76 76 81 88
 96: 26068688    70 76 77 82 88
 97: 28180781    71 77 78 83 89
 98: 30496934    72 78 79 84 90
 99: 33092587    73 79 80 85 91
100: 35924570    74 80 81 86 92

其中，n≤32的结果与之前做出来的结果完全吻合。
从表中可以看出五个参数均有良好的单调性和平滑性。
利用a,b,c,d,e的单调性和平滑性，可将时间复杂度优化为O(n)。
优化后可以计算很大的n，用来观察数据的增长趋势。
计算到n=100000，结果如下：

     n   log(f(n))      d     e     c     a     b
--------------------------------------------------
    10:   2.534026      3     4     5     6     7
   100:   7.555392     74    80    81    86    92
  1000:  22.358183    914   935   936   956   977
 10000:  68.093119   9724  9793  9793  9861  9930
100000: 211.641457  99125 99344 99344 99562 99781

上述结果很可能不是最终结果，但可以作为最终结果的一个很好的上界。
因为当n>32时，很可能会有新的移动模式出现。
而当前的移动模式仅仅只是新的移动模式的一个特例。
新的移动模式会在当前的基础上新增若干个参数，把当前的移动模式更为一般化。
所以接下来的工作是尝试寻找新的移动模式，看看上述结果能不能继续优化。
如果找不到新的移动模式，则说明上述结果就是最终结果，对其加以证明就完美解决问题了。

最终他把结果提交到OEIS形成了A160002.

n	f(n)
0	0
1	3
2	10
3	19
4	34
5	57
6	88
7	123
8	176
9	253
10	342
11	449
12	572
13	749

n	f(n)
0	0
1	3
2	10
3	19
4	34
5	57
6	88
7	123
8	176
9	253
10	342
11	449
12	572
13	749

n	f(n)
0	0
1	3
2	10
3	19
4	34
5	57
6	88
7	123
8	176
9	253
10	342
11	449
12	572
13	749