自然数分家 - 威佐夫博弈和Beatty定理

PKU-1067是一个石子游戏，这其实是一个威佐夫博弈问题, 英文维基百科 也有详尽描述。
问题的大概描述是: 有两堆各若干个物品，两个人轮流从某一堆或同时从两堆中取同样多的物品，规定每次至少取一个，多者不限，最后取光者得胜。
如果两堆余下物品分别在下面图标中数目时：

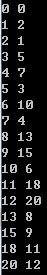
是接下去先手会输的局面，我们称这种问题中的必败态为奇异局势$(a_k,b_k)$。
可以看到，$a_0=b_0=0$，$a_k$是未在前面出现过的最小自然数，而$b_k=a_k+k$。
进一步分析可以发现：
任何自然数都包含在一个且仅有一个奇异局势中，
由于$a_k$是未在前面出现过的最小自然数，所以有$a_k \gt a_{k−1}$。
$b_k=a_k+k\gt a_{k−1}+k\gt a_{k−1}+k−1=b_{k−1}\gt a_{k−1}$。
其中$a_k=\lfloor k\omega\rfloor$, 其中$\omega^2=\omega+1$,即$\omega = 1.618\dots$即所谓黄金分割数，而$b_k=\lfloor k\psi\rfloor$,其中$\psi=\omega+1$。
实际上$a_n$和$b_n$构成了一个Beatty序列。

Beatty定理

设$a，b$是正无理数且$\frac1a+\frac1b=1$
记$P=\{\lfloor na\rfloor|n为任意的正整数\}，Q=\{\lfloor nb\rfloor|n为任意的正整数\}$
（$\lfloor x\rfloor$指的是不好过$x$的最大整数）
则$P$与$Q$是$Z^{+}$的一个划分，即$P∩Q$为空集且$P∪Q$为正整数集合$Z^{+}$。

即对于任意满足条件的无理数$a,b$, 数列$\lfloor na\rfloor$和$\lfloor nb\rfloor$实现了正整数集的完美分家。

三家分赵

王守恩在2019年10月询问 ，$\{a(n)\}\cup\{b(n)\}\cup\{c(n)\}$正好构成正整数集吗？为什么？ 其中:
{a(n)}={1, 4, 07, 09, 12, 15, 16, 19, 22, 25, 27, 30, 32, 34, 37, 40, 43, 45, 47, 50, 52, 55, 58, 60, 63, 65,...}
{b(n)}={2, 5, 08, 11, 14, 18, 20, 23, 26, 29, 33, 36, 38, 41, 44, 48, 51, 54, 56, 59, 62, 66, 69, 72, 75, 77,...}
{c(n)}={3, 6, 10, 13, 17, 21, 24, 28, 31, 35, 39, 42, 46, 49, 53, 57, 61, 64, 67, 71, 74, 79, 82, 85, 89, 92,...}

$a(n)=n+\lfloor n\sqrt[4]{\frac12}\rfloor+\lfloor n\sqrt[4]{\frac14}\rfloor$

$b(n)=n+\lfloor n\sqrt[4]{\frac12}\rfloor+\lfloor n\sqrt[4]{2}\rfloor$

$c(n)=n+\lfloor n\sqrt[4]{4}\rfloor+\lfloor n\sqrt[4]{2}\rfloor$

lsr314分析发现 , 貌似只要$t\gt 0$且$t^2,t+\frac1t,t+t^2,\frac1t+\frac1{t^2}$都是无理数，那么 $a_n=n+\lfloor\frac nt\rfloor+\lfloor\frac n{t^2}\rfloor,b_n=n+\lfloor\frac nt\rfloor+\lfloor nt\rfloor,c_n=n+\lfloor\frac n{t^2}\rfloor+\lfloor nt\rfloor,$ $\lfloor x\rfloor$表示$x$的整数部分，那么每个正整数刚好在$a_n,b_n,c_n$中出现一次。本题中$t=2^{\frac14}$。

群雄逐鹿

王守恩继续问， 还可以有 $\{a(n)\}\cup\{b(n)\}\cup\{c(n)\}\cup\{d(n)\}$正好构成正整数集吗？

lsr314继续做出解答
如果$t_1,t_2,…,t_k$都是正数，且任意两个数的比值都是无理数，
$a_i(n)=\sum_{j=1}^k\lfloor\frac{t_j}{t_i} n\rfloor,i=1,2,…k.$ 那么每个正整数在数列$a_1(n),…a_k(n)$中恰好出现一次。

自然数大分家 - Fibonacci矩阵

mathe在csdn的博客 中, 如下定义一个无限阶矩阵m：
矩阵第0行正好是Fibonacci数列，也就是 $m_{0,0}=1,m_{0,1}=2,m_{0,2}=3, m_{0,3}=5,m_{0,4}=8,\dots$ 矩阵第k行中第一个数字是前面k-1行中都没有出现的最小正整数, 所以 $m_{1,0}=4, 而m_{k,1}=2m_{k,0}-k$ (这个关系对于第0行也成立), 比如$m_{1,1}=2\times4-1=7$。
而第k行后面的任意一个数的递推关系同第一行类似,是当前行前面两个数的和。
比如$m_{1,2}=m_{1,0}+m_{1,1}=11,\dots$
于是我们可以得到如下的Fibonacci矩阵

$\begin{matrix} 1&2&3&5&8&13&21&34&55&89&144&\dots\\ 4&7&11&18&29&47&76&123&199&322&521&\dots\\ 6&10&16&26&42&68&110&178&288&466&754&\dots\\ 9&15&24&39&63&102&165&267&432&699&1131&\dots\\ 12&20&32&52&84&136&220&356&576&932&1508&\dots\\ 14&23&37&60&97&157&254&411&665&1076&1741&\dots\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\ddots \end{matrix}$

我们可以神奇的发现，这个矩阵正好包含了所有的自然数，而且每个自然数只出现一次，它实现了正整数集更大的分家。
链接中还提出了如下一些问题:
问题1)
我们计算所有的$m_{k+1,0}-m_{k,0}$,我们可以得到如下序列:
32332...
证明或否定:所有的$m_{k+1,0}-m_{k,0}$必然是2或者3.
问题2)
我们在一张白纸上先写下
32
两个数
然后从这行数第一个数字开始查看,每看到一个3,在后面添加三个数332;每看到一个2,在后面添加两个数32,
比如第一次操作,由于第一个数是3,添加332,所以数列变成:
32332
第二次操作,由于第二个数是2,添加32,所以数列变成
3233232
第三次操作,由于第三个数是3,添加332,所以数列变成
3233232332
一直这样下去
证明或否定,这样得到的一个序列正好是(1)中由所有$m_{k+1,0}-m_{k,0}$顺序排成的序列.
这个方法给出了一种快速构造上面矩阵的方案。