二十棵树最优解求解问题

Thu, 12th December 2019Edit on Githubbash 果树问题

简介

20棵树植树问题是一个关于将20棵树(每棵树看成一个点)种在一个平面果园中，要求每行正好四棵树的行数尽量多的数学问题。比如:
n23
这个问题来源于Orchard Planting Problem, 或者英文维基百科果树问题上也有介绍。原始问题是要求将n棵树种在一个平面果园中，要求每行k棵树的行数尽量多。
这个问题中每行3棵树的情况已经有非常好的结果: B. Grunbaum和Sloane在1974年通过复杂的数学理论（椭圆曲线）给出了很好的下界，不少于 $1+⌊\frac{n^2}6-\frac{n}2⌋$ 行; 而G. Ben和陶哲轩在2013年证明了对于充分大的n,上面方法给出的已经是最优解。
但是对于每行4棵或更多树的情况，现在我们还没有得出很好的结果。其中20棵树每行四棵的问题不知道为何，在国内互联网广为流传, 形成了20棵树植树问题。
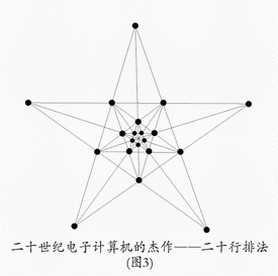
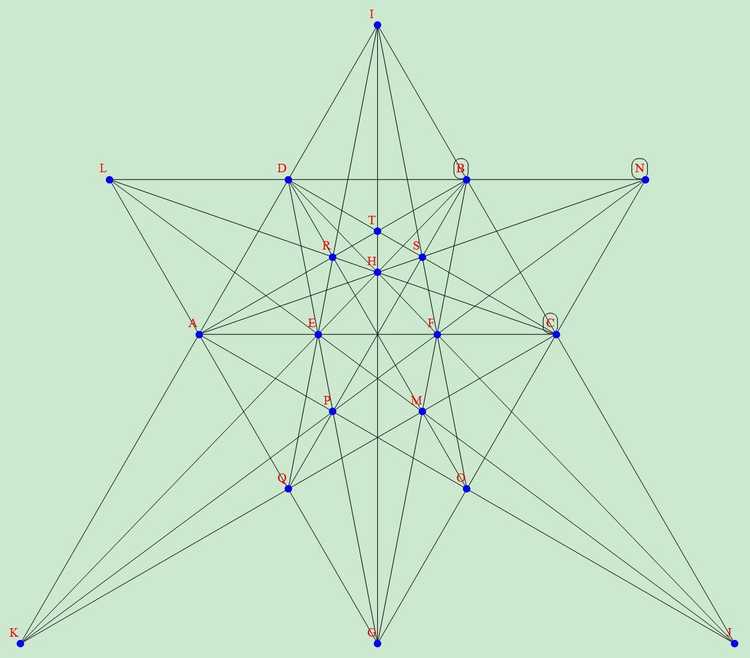
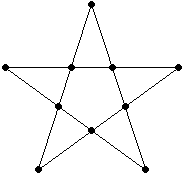
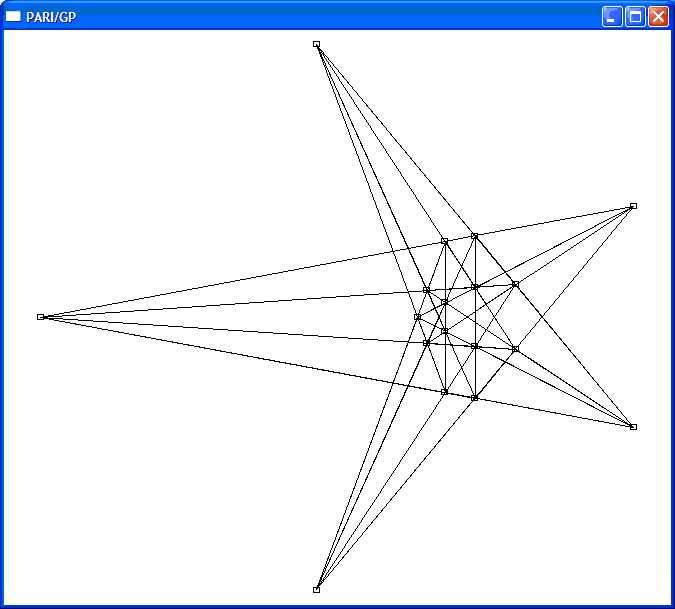
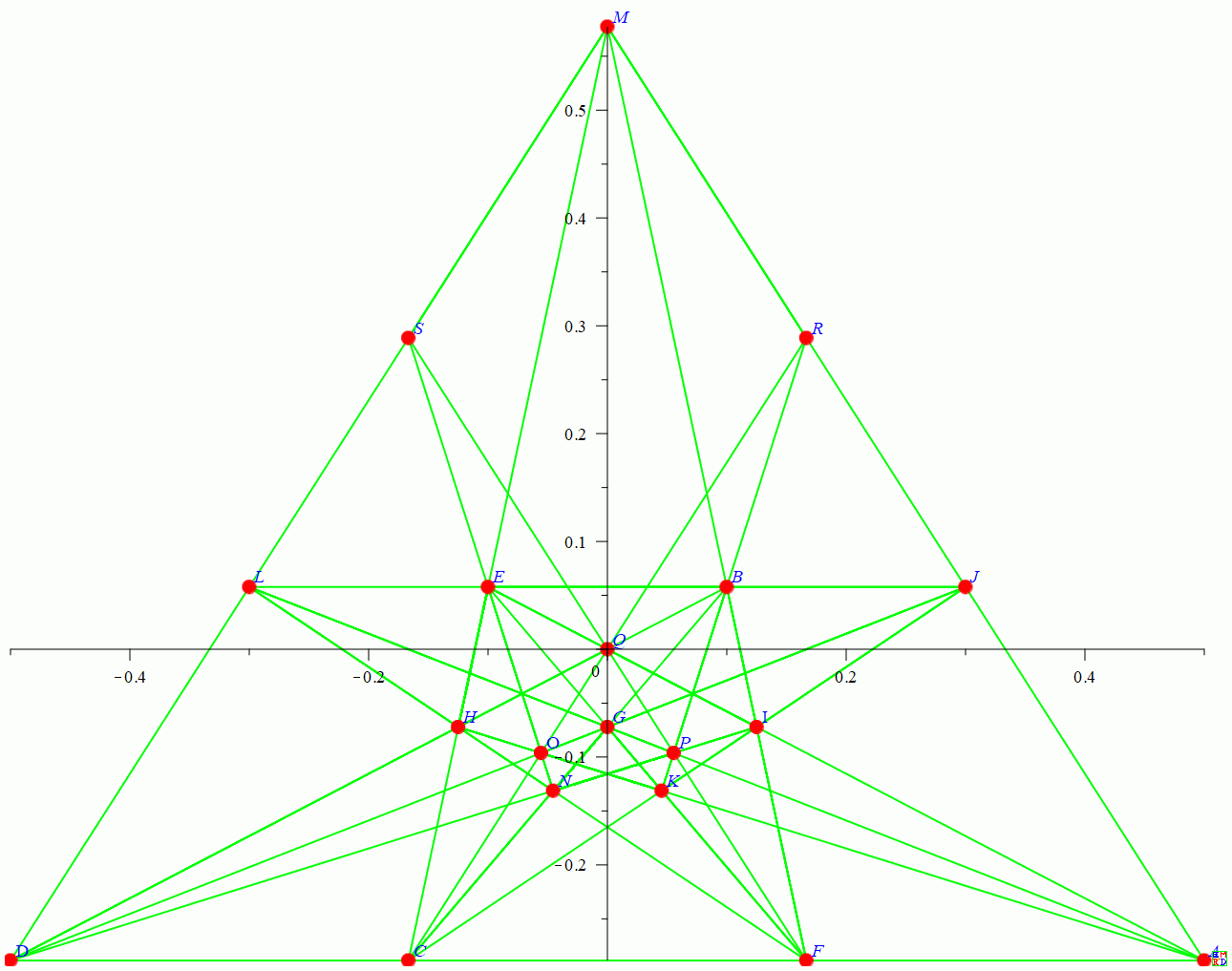
网络上流传着一个非常漂亮多层正五角星嵌套的20行结果（计算机搜索结果），不过这个远远不是最优解：
20rows
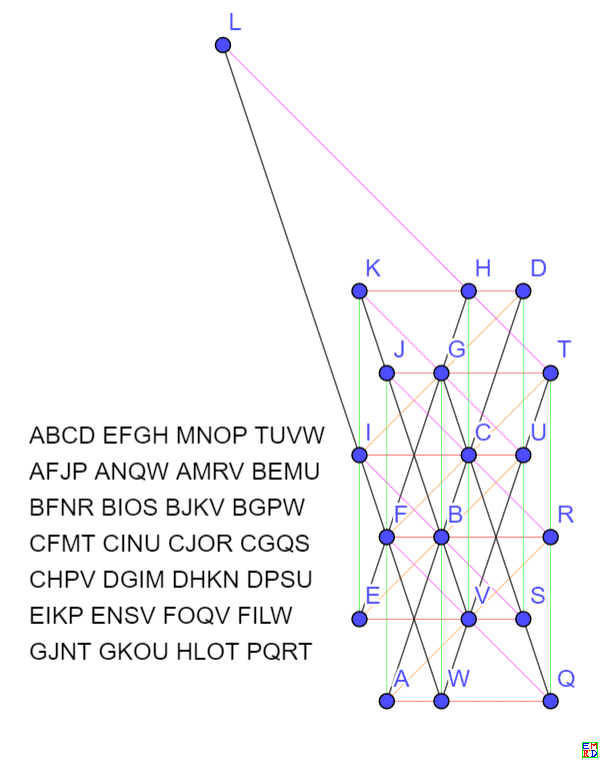
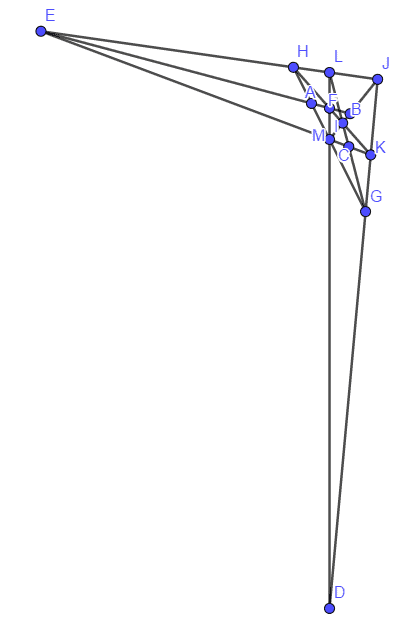
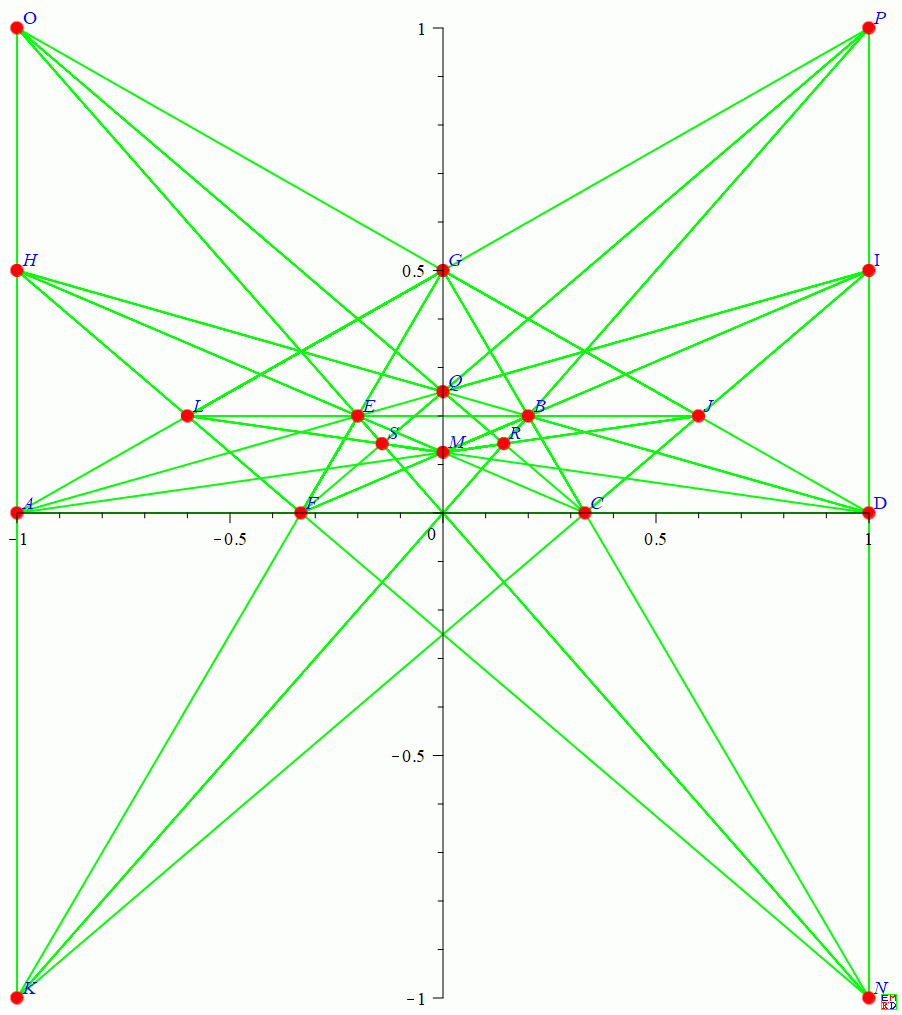
2005年，Xianzu Lin (可以能是福建师范大学的林贤祖教授)最早给出了一种20棵树23行的方案(图上缺了直线KQRL)，只是给出的图中部分点为无穷远点，非数学专业人员难以理解（后面我们会介绍如何将结果转化为更加容易看懂的等价结果）。可能因为这个原因，这个结果并没有怎么流传开来。
xianzu
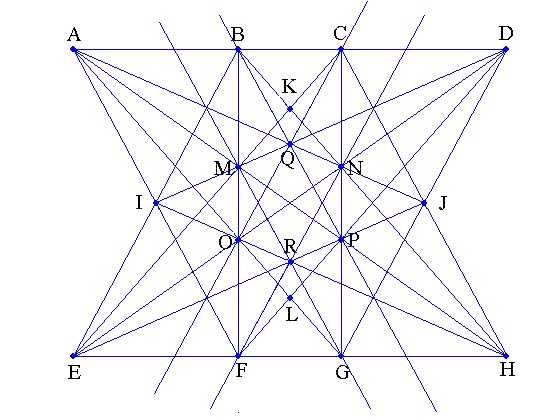
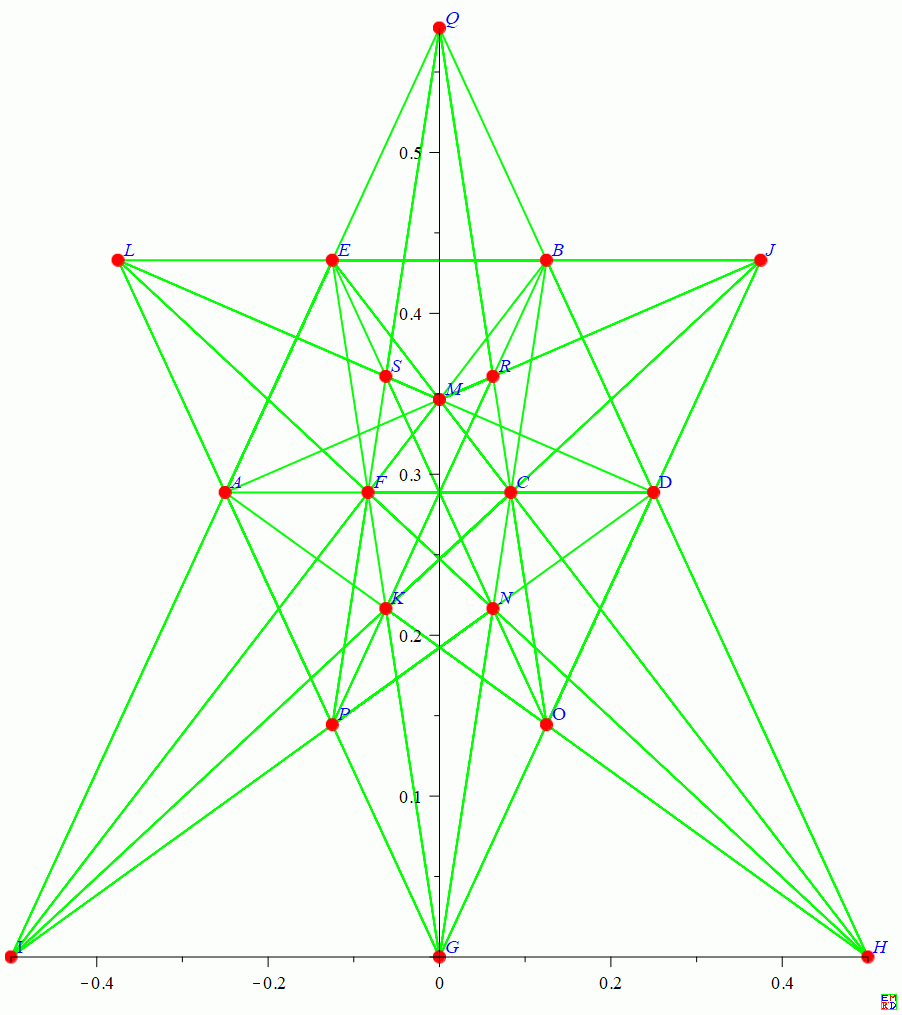
2006年，辽宁锦州开发区笔架山小学的王兴君成功地绘制出了一个欧氏平面中23行图，这个结果在国内网络上流传比较广泛
xwang
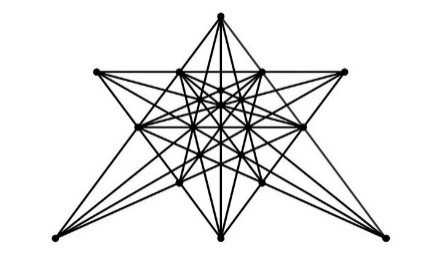
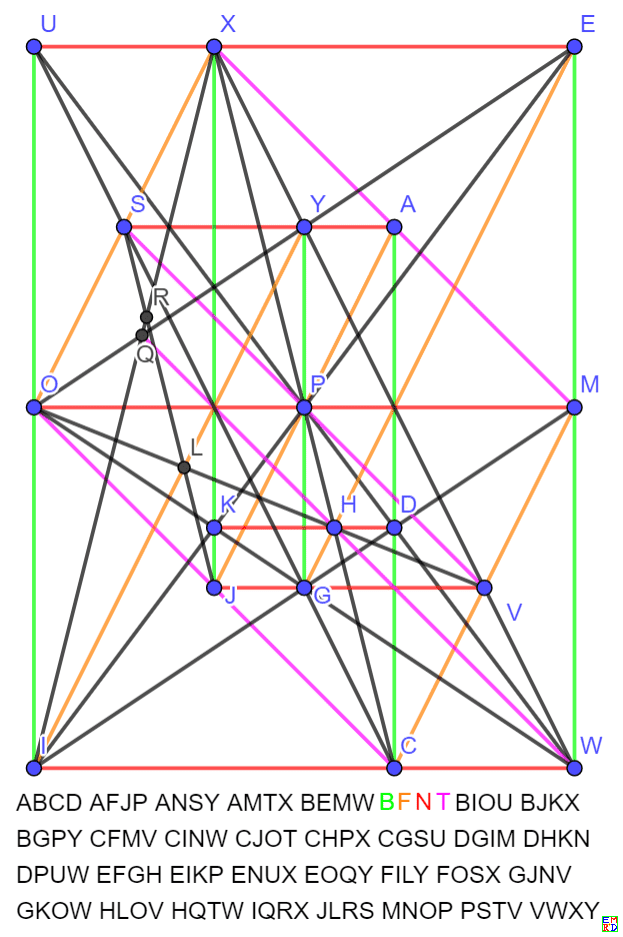
2009年，河北省邢台学院学生黄阳阳（昵称eyond）成功地绘制出了另一个漂亮的23行植树图，结果如下：
xwang
2010年2月，我们在数学研发论坛上通过多人协作，共同使用多台计算机验证了20棵树每行四棵树，最多只能种植23行。但是限于计算能力，我们还无法找出所有的23行解。程序只找到了两种不等价的解，其中一个解和Xianzu Lin的结果等价，而另外一组解和王兴君和黄阳阳的都等价。其中王兴君和黄阳阳的结果虽然看似不同，但是从数学中的射影变换的角度来看，是可以相互转化的。
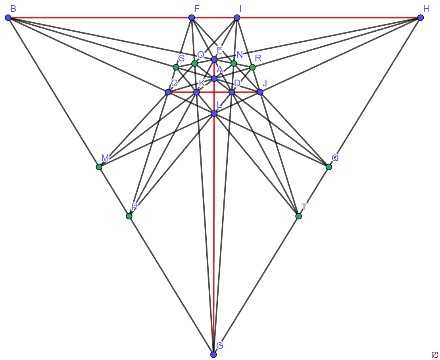
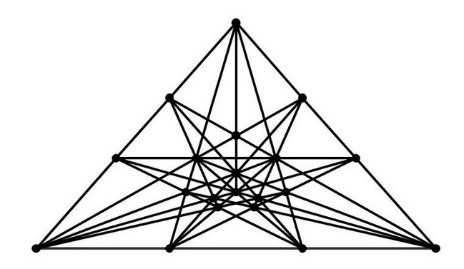
2019年9月，我们利用计算机又找出一种和上面两种方案都不等价的新的23行解。可以看出，这个解过每棵果树都至少有4行，而Lin的方案有两棵树只有3行经过，王和黄的方案有一棵树只有三行经过，所以这个解必然和它们不同。
n23
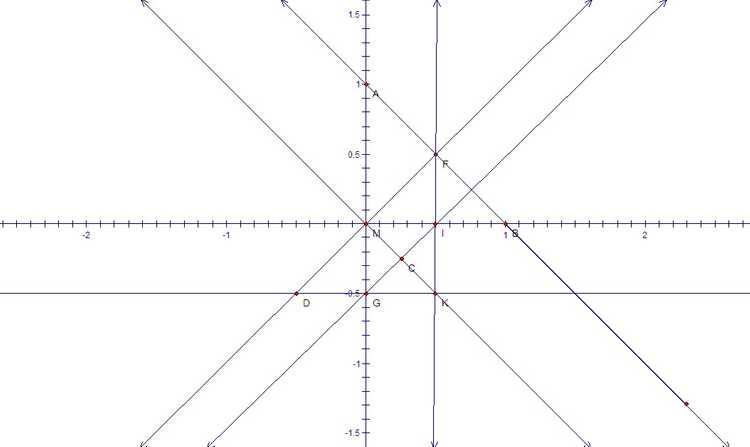
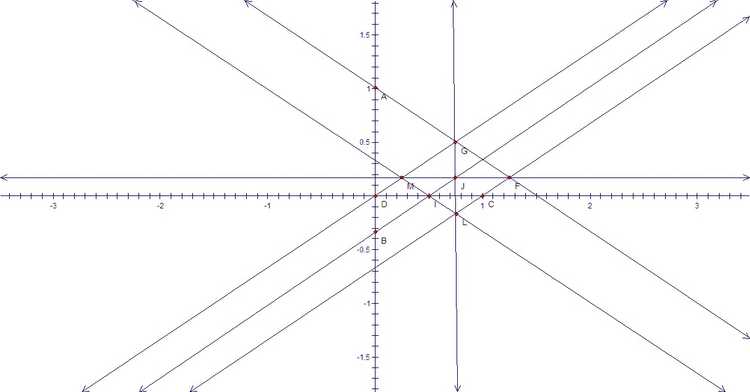
而这个解还可以画成下面两种不同的形式:
s20f
302
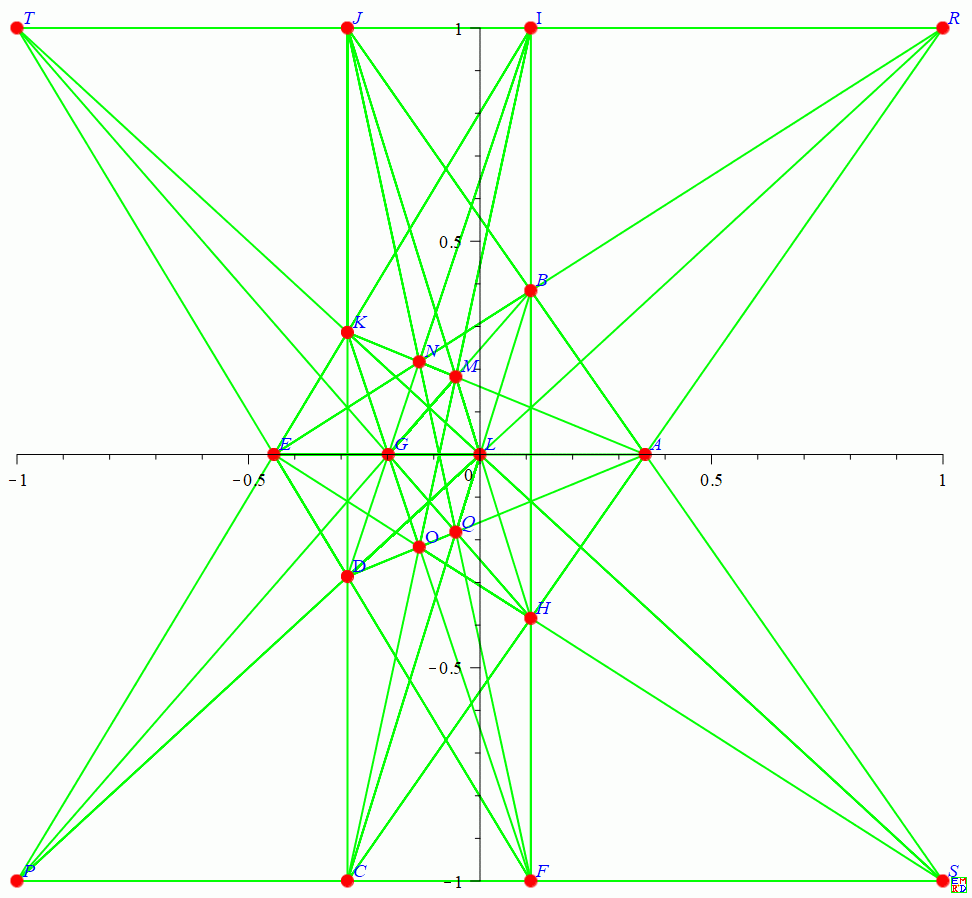
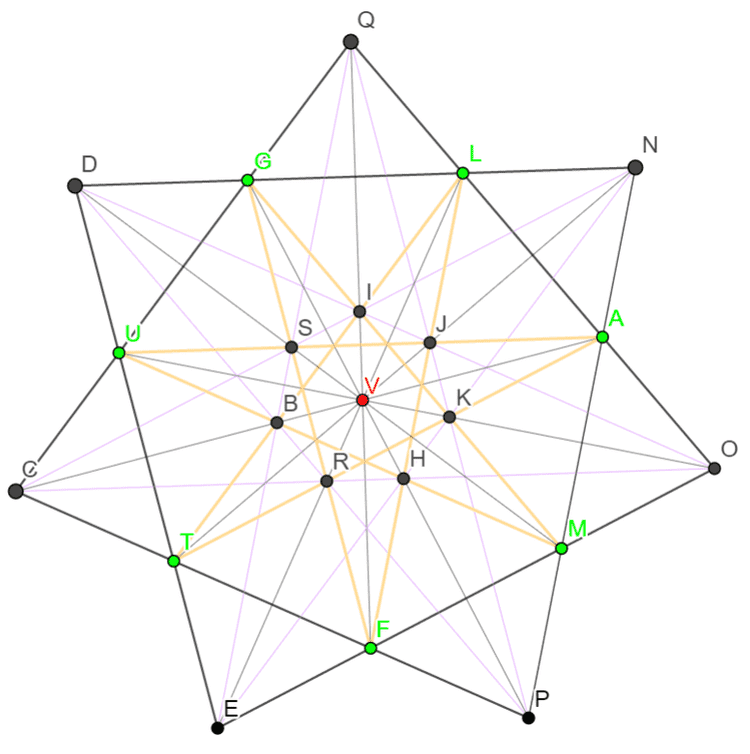
从数学角度，我们可以通过射影变换将上面这些图片进行变换得出一些等价的但是看似不同的结果，比如2012年1月wayne就将前两种23行结果经过射影变换变化出如下一些漂亮的图片，下面只给出四个图片，对应链接中含有更多的等价漂亮图片。

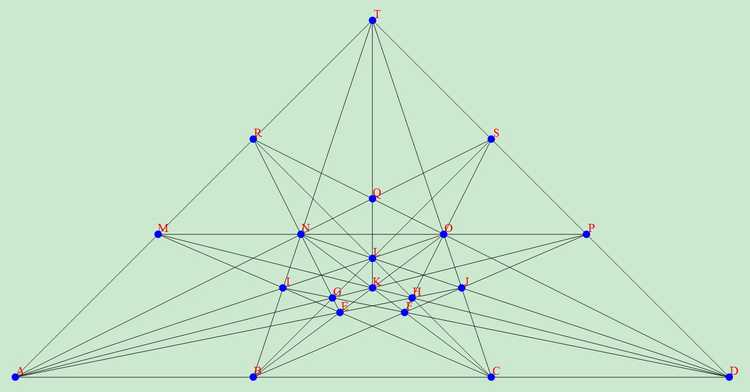
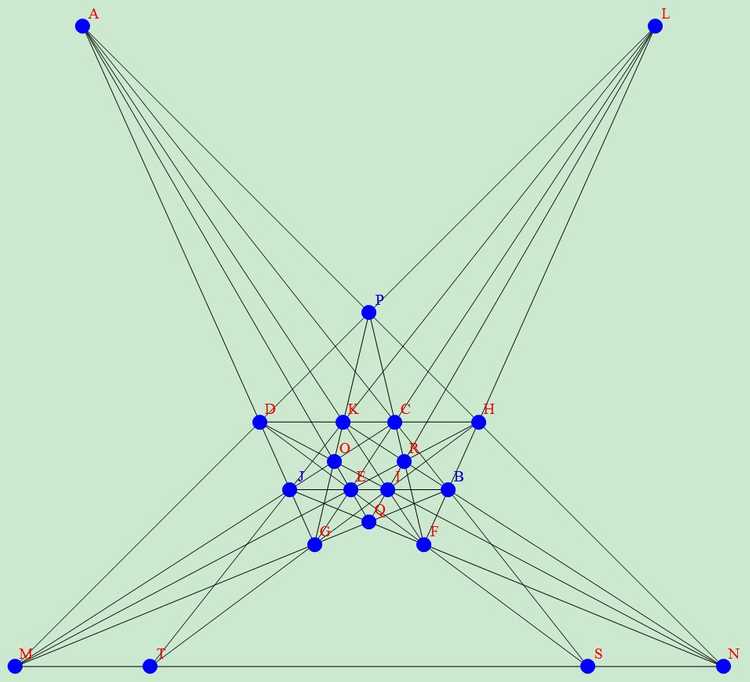
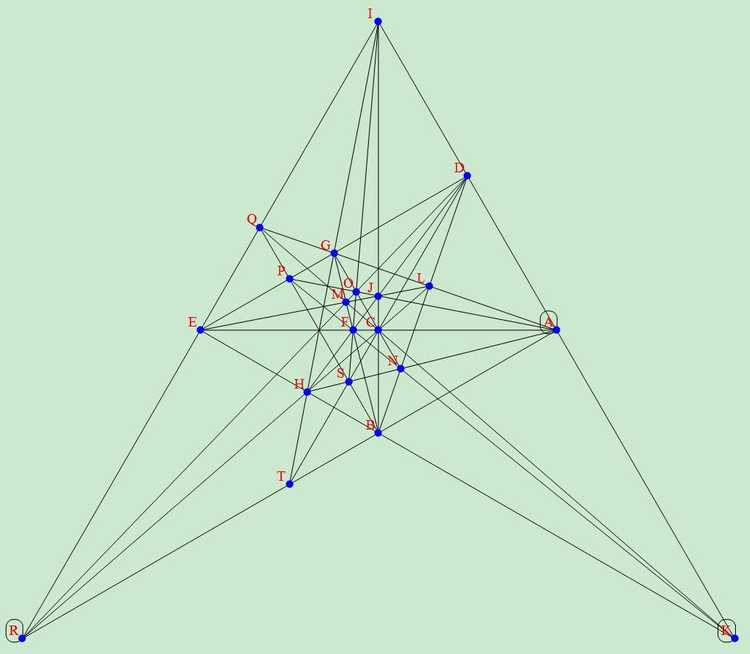
2019年12月，我们还发现了一个漂亮对称的22棵树28行解:
w22.7

射影变换介绍

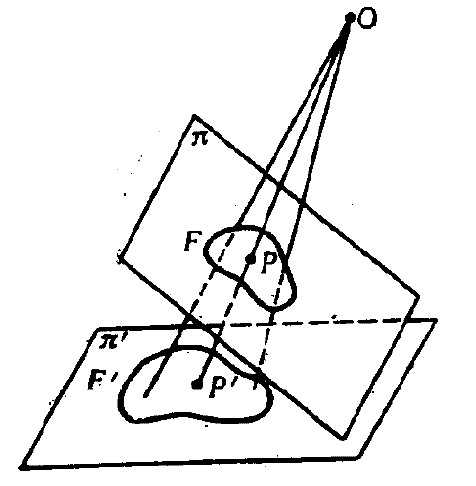
如果我们观察圆盘在地面上的影子，我们会发现圆形的圆盘会被投影成椭圆形的; 也就是在投影变换下，图片的形状会发生变换。而且随着点光源，圆盘和投影平面位置的变化，我们甚至还可以将圆盘投影为抛物线和双曲线。但是可以看出，在投影下，直线的投影还是直线，并且投影也不会改变直线系中交点和直线的相关关系。所以如果我们得到了一个二十棵树问题的解，那么通过投影变换就可以转化出无数幅看似不同的结果。比如王兴君和黄阳阳的答案看似不同，本质相同。
proj
在网页射影几何简介中给出了射影变换的介绍。而为了能够通过数值计算的方案对上面这些结果进行射影变换转化出更多的结果，我们首先需要理解齐次坐标这个概念。
在平面坐标系中，任何一个点可以通过其横坐标和纵坐标值(x,y)来确定。对于这样的一个点，在对应的齐次坐标系中，我们需要使用[rx : ry : r]来表示，其中参数r可以是任意非零的实数。也就是说，任何一个点在齐次坐标系下其表示形式是不唯一的，可以有无穷种形式。比如平面坐标系上点(-1,1)在对应的齐次坐标系下可以写成[-1 : 1 : 1],也可以表示为[-2 : 2 : 2]等等。
齐次坐标系的最大好处是可以描述无穷远点。在平面几何中，两条直线可以有平行和相交两种关系。但是在射影几何中，任何两条直线相交于唯一的一点。其中，平面几何中平行的两条直线在射影几何中相交于一个无穷远点。所有无穷远点的齐次坐标形式中第三个分量总是0。比如所有和横坐标平行的直线相交于无穷远点[1 : 0 : 0],而所有和纵坐标平行的直线相交于无穷远点[0 : 1 : 0]。所有的无穷远点构成一条无穷远直线Z=0。

对于一个平面图案，如果我们选择一个3×3可逆矩阵 $A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33} \end{pmatrix}$ ,那么对于射影平面上任意一个点 $[x:y:z]$ , 变换 $[x^{\prime}:y^{\prime}:z^{\prime}]= [x:y:z]A$ 就对应一个投影变换; 也就是 $\begin{cases}x^{\prime}=a_{11} x+a_{21} y+a_{31} z\\y^{\prime}=a_{12} x+a_{22} y+a_{32} z\\z^{\prime}=a_{13} x+a_{23} y+a_{33} z\end{cases}$ , 或者对应平面坐标系下的变换（如果没有无穷远点参与） $\begin{cases}x^{\prime}=\frac{a_{11} x+a_{21} y+a_{31}}{a_{13} x+a_{23} y+a_{33} }\\y^{\prime}=\frac{a_{12} x+a_{22} y+a_{32}}{a_{13} x+a_{23} y+a_{33} }\end{cases}$ 。
wanye通过一个简单的mathematica代码给出了将二十棵树问题的一个解随机投影成另外一些形式。其中，通过将无穷远直线投影成普通直线可以使得得到的图看上去和原先的图完全不同。

四点确定一个射影变换矩阵

给定平面上任意三点不共线的四个点在射影变换前后的坐标，就可以唯一确定对应的射影变换，计算方法如下 :
设变换前的存在四点坐标 $Q=[Q_1,Q_2,Q_3],V=[V_1,V_2,V_3],U=[U_1,U_2,U_3],N=[N_1,N_2,N_3]$

变换后的四点坐标 $Q1=[Q1_1,Q1_2,Q1_3],V1=[V1_1,V1_2,V1_3],U1=[U1_1,U1_2,U1_3],N1=[N1_1,N1_2,N1_3]$

构造 $12\times 13$ 阶矩阵：

T = \begin{pmatrix} Q_{1}&Q_{2}& Q_{3}&0&0&0&0&0&0&Q1_{1}&0&0&0\\ 0&0&0&Q_{1}&Q_{2}&Q_{3}&0&0&0&Q1_{2}&0&0&0\\ 0&0&0&0&0&0&Q_{1}&Q_{2}&Q_{3}&Q1_{3}&0&0&0\\ V_{1}&V_{2}&V_{3}&0&0&0&0&0&0&0&V1_{1}&0&0\\ 0&0&0&V_{1}&V_{2}&V_{3}&0&0&0&0&V1_{2}&0&0\\ 0&0&0&0&0&0&V_{1}&V_{2}&V_{3}&0&V1_{3}&0&0\\ U_{1}&U_{2}&U_{3}&0&0&0&0&0&0&0&0&U1_{1}&0\\ 0&0&0&U_{1}&U_{2}&U_{3}&0&0&0&0&0&U1_{2}&0\\ 0&0&0&0&0&0&U_{1}&U_{2}&U_{3}&0&0&U1_{3}&0\\ N_{1}&N_{2}&N_{3}&0&0&0&0&0&0&0&0&0&N1_{1}\\ 0&0&0&N_{1}&N_{2}&N_{3}&0&0&0&0&0&0&N1_{2}\\ 0&0&0&0&0&0&N_{1}&N_{2}&N_{3}&0&0&0&N1_{3} \end{pmatrix}_{12 \times 13 }

然后求解 $TR=0$ 的非零解 $R=[R_1,R_2,R_3,R_4,R_5,R_6,R_7,R_8,R_9,R_{10},R_{11},R_{12}, R_{13}]$

(maple的求解命令为NullSpace, Pari/gp使用matker命令）

则可以得到变换矩阵S为

S = \begin{pmatrix} R_1&R_2&R_3\\ R_4&R_5&R_6\\ R_7&R_8&R_9 \end{pmatrix}_{3 \times 3 }

分析思路如下，
设变换矩阵 $S=\begin{pmatrix}R_1&R_2&R_3\\R_4&R_5&R_6\\R_7&R_8&R_9\end{pmatrix}$ 将
$Q=\begin{pmatrix}Q_1\\Q_2\\Q_3\end{pmatrix},V=\begin{pmatrix}V_1\\V_2\\V_3\end{pmatrix},U=\begin{pmatrix}U_1\\U_2\\U_3\end{pmatrix},N=\begin{pmatrix}N_1\\N_2\\N_3\end{pmatrix}$ 变换为 $Q1=\begin{pmatrix}Q1_1\\Q1_2\\Q1_3\end{pmatrix},V1=\begin{pmatrix}V1_1\\V1_2\\V1_3\end{pmatrix},U1=\begin{pmatrix}U1_1\\U1_2\\U1_3\end{pmatrix},N1=\begin{pmatrix}N1_1\\N1_2\\N1_3\end{pmatrix}$
于是存在常数 $-R_{10},-R_{11},-R_{12},-R_{13}$ 使得
$SQ=-R_{10} Q1,SV=-R_{11} V1， SU=-R_{12} U1, SN=-R_{13} N1$
展开后就出现前面的矩阵 $T$ 了,即
$T\begin{pmatrix}R_1\\R_2\\R_3\\R_4\\R_5\\R_6\\R_7\\R_8\\R_9\\R_{10}\\R_{11}\\R_{12}\\R_{13}\end{pmatrix}=0$ .
所以解这个方程得出任意的非零向量，取前9个分量构成矩阵S即可。

计算机求解算法简介

由于搜索20棵树问题最优解的计算量非常大，我们使用了很多技巧来解决这个问题。这个算法首先构造了一些使用较少树的方案，然后通过每次逐步添加一棵额外的树，得到包含更多树的方案。计算过程中采用了齐次坐标，由此可以事先任意设定其中四个三点不共线点的坐标（射影变换可以将任意三点不共线的四个点坐标任意投影）。

算法总体介绍的第三步中给出了一种对于给定两个看似不同的点线关系图，判断它们是否等价（通过交换点或线的顺序）的算法。在添加树的搜索扩张过程中，如果我们发现两个图（包含了若干树）是等价，就可以淘汰掉其中一个图，不需要继续搜索从它派生的图，从而节省了大量的计算时间。

另外对于给定的一种点线关系图（特别是包含的行很多时），无法保证一定存在对应的果树问题解。算法总体介绍还描述了一种通过消元来简化方程组，最后可以部分确认/简化或淘汰某些关系是否存在对应的果树问题解。这个算法不仅仅在我们得到一种合法的果树问题解的点线关系后，可以用于求出最终的坐标，也可以在上述搜索过程中，提前淘汰一些没有对应果树问题解的看似合法的点线关系，从而也缩小了搜索空间，节省大量的计算时间。
通过使用上述的算法，使用计算机已经可以解决13棵树和14棵树问题，但是对于20棵树问题还远远不够。

9~12棵树

t10
t11
t12

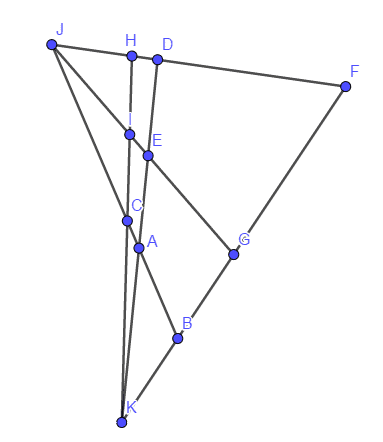
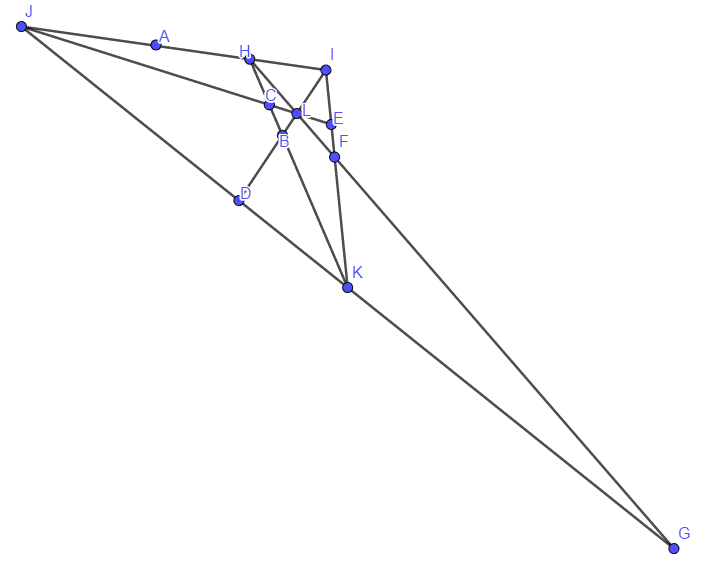
13棵树

t13
13棵树问题的解（9行，包含无穷远直线）

ABEFAGHMBIJMCEKMCGILDFLMDGJKEHJLFHIK
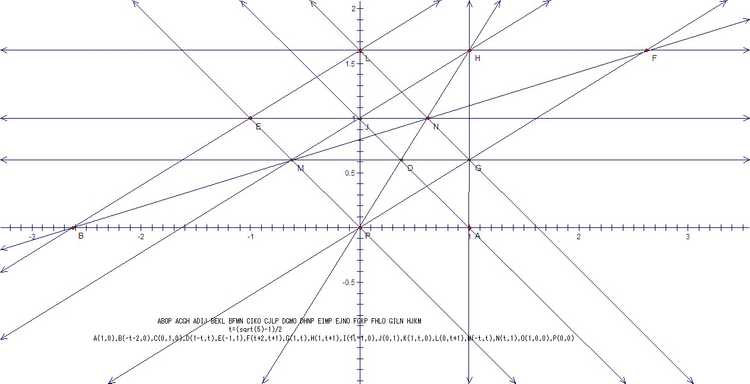
A(0,1) B(1,0) C(1/4,-1/4) D(-1/2,-1/2) E[1 : -1 : 0] F(1/2,1/2) G(0,-1/2) H[0 : 1 : 0] I(1/2,0) J[1 : 0 : 0] K(1/2,-1/2) L[1 : 1 : 0] M(0,0)

经过射影变换可以转化为只含一个无穷远点的对称图形 :
s13
还可以有没有无穷远点的
n13

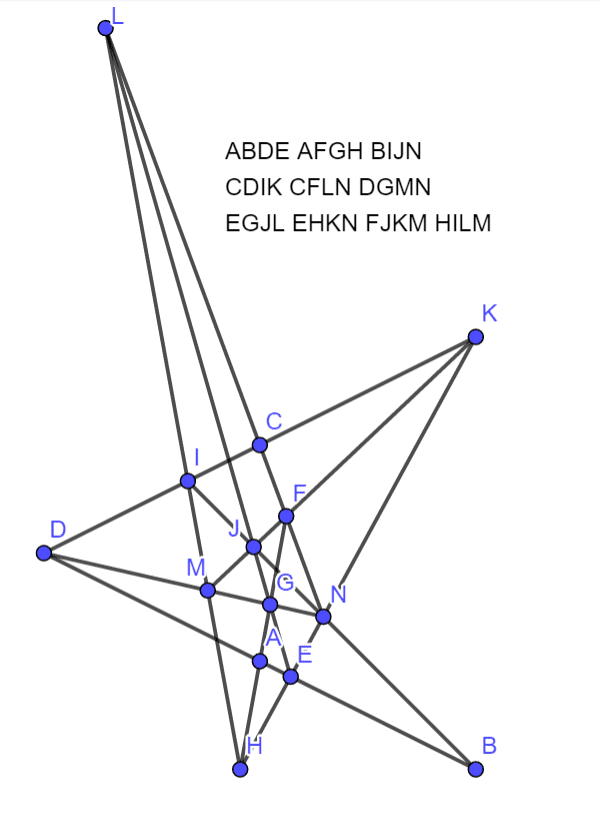
14棵树

t14
14棵树问题的解（10行，包含无穷远直线）

ABDEAFGHBIJNCDIKCFLNDGMNEGJLEHKNFJKMHILM
solve([-4/3+1\times K_X,-8/3+1\times L_X,+3+1\times L_Y,+9/4+1\times J_Y,+2+1\times K_Y,+3/2+1\times I_Y,+1+1\times H_Y,-3+1\times G_Y,+4+1\times C_Y,+5+1\times F_Y,-4/3+1\times H_X,-8/3+1\times C_X,-8/3+1\times F_X,-4/3+1\times E_X],[K_X,L_X,L_Y,J_Y,K_Y,I_Y,H_Y,G_Y,C_Y,F_Y,H_X,C_X,F_X,E_X]);
print("A_x=1 A_y=0 B=[1:0:0] D_x=0 D_y=0 E_y=0 G_x=0 I=[1:I_y:0] J=[1:J_y:0] M_x=0 M_y=1 N=[0:1:0] ");

去除无穷远点可以转化为:
s14
上面的图无法转化为对称图，但是14棵树10行有很多解，其中下面是一个对称图 :
s14.1
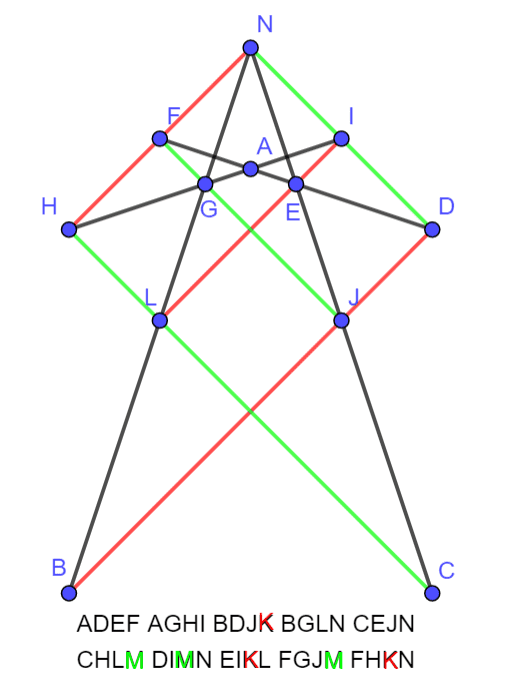
还可以去除无穷远点转化为:
s14.3
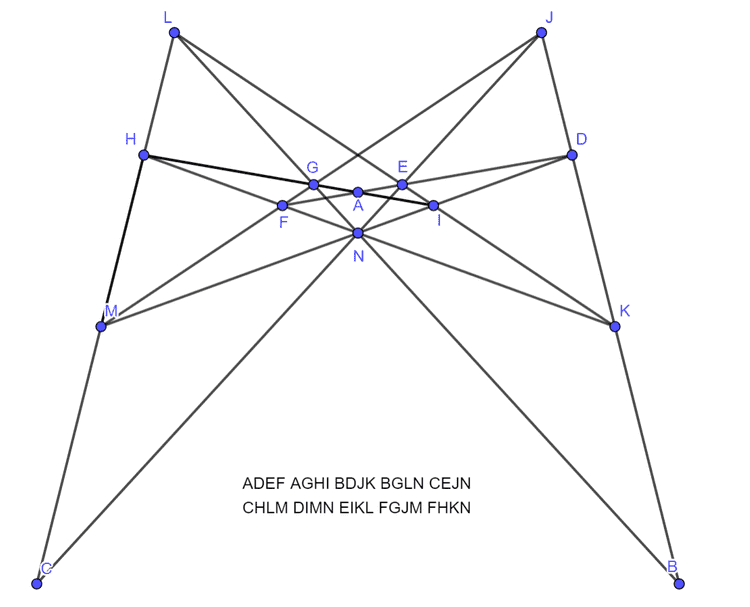
数学星空后来给出更多14棵10行图

后来，我们进一步提供了一种可以只搜索包含线的数目比较多的方案，再次加速了搜索过程，使得我们能够解决到17棵树的问题。

15棵树

t15
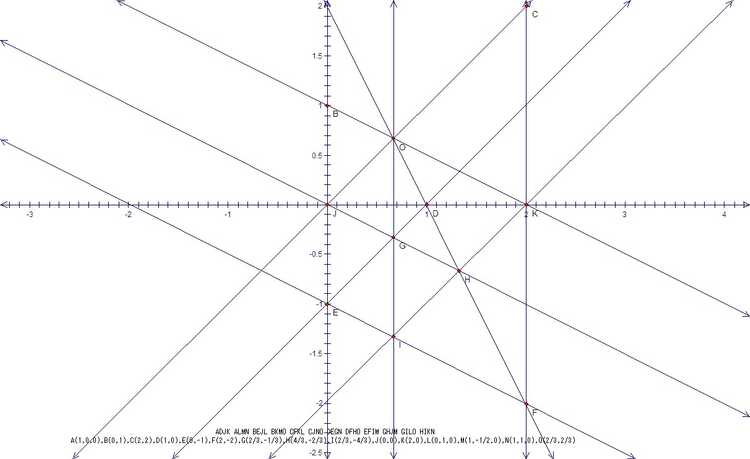
15棵树问题的最优解
还可以有对称解
15.5
15.6
15.7
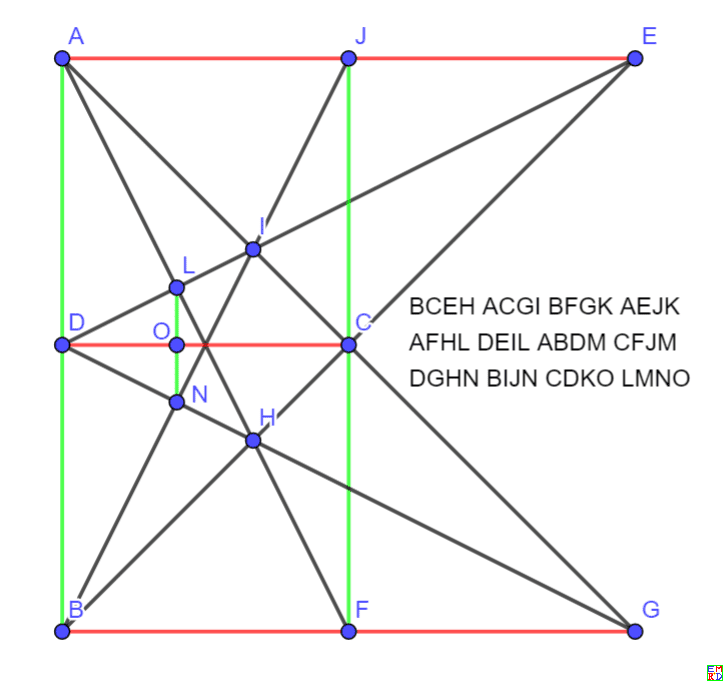
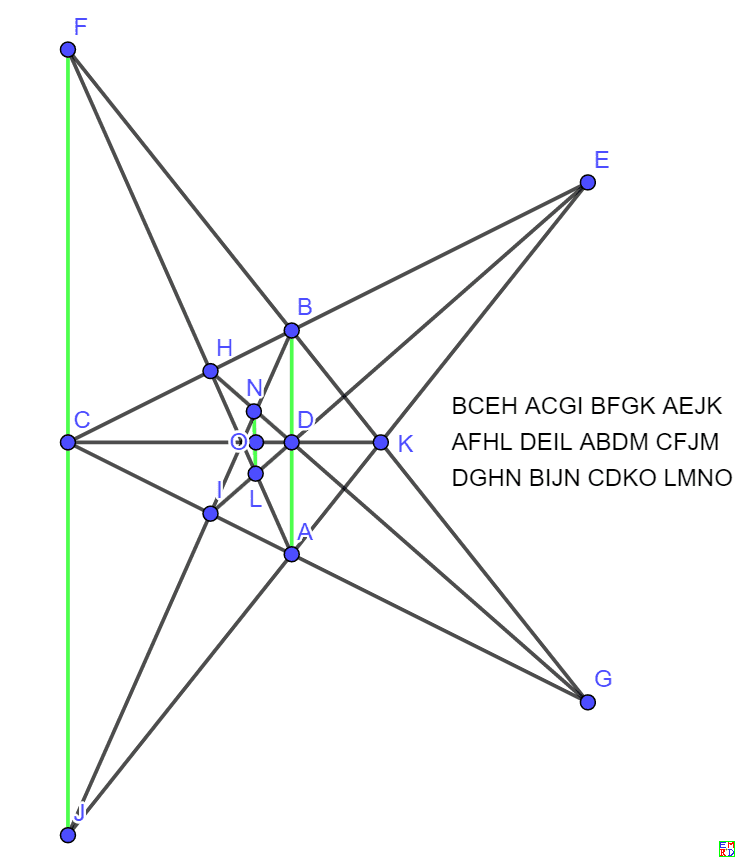
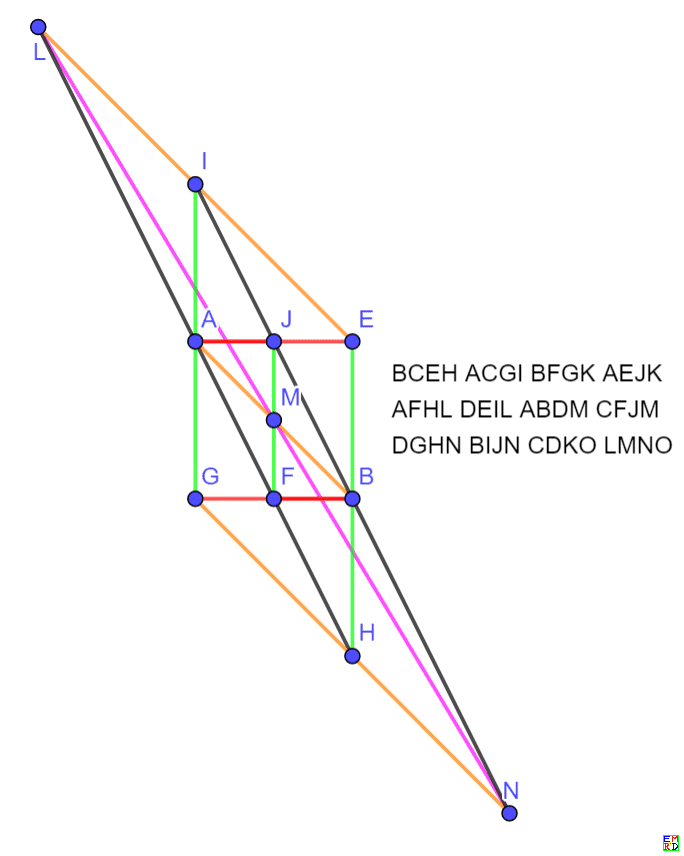
以及旋转对称解
15.s1
旋转飞镖解 15.s2
数学星空后来给出了更多15棵12行的解。

16棵树

t16
16棵树问题的最优解对称形式
s16
还有超级对称解
22-51-33-4pt16
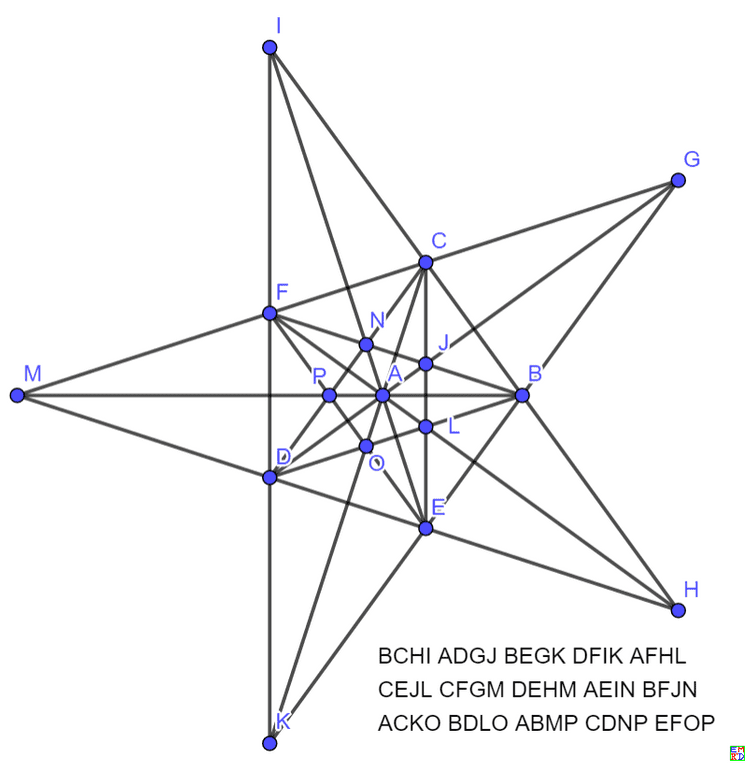
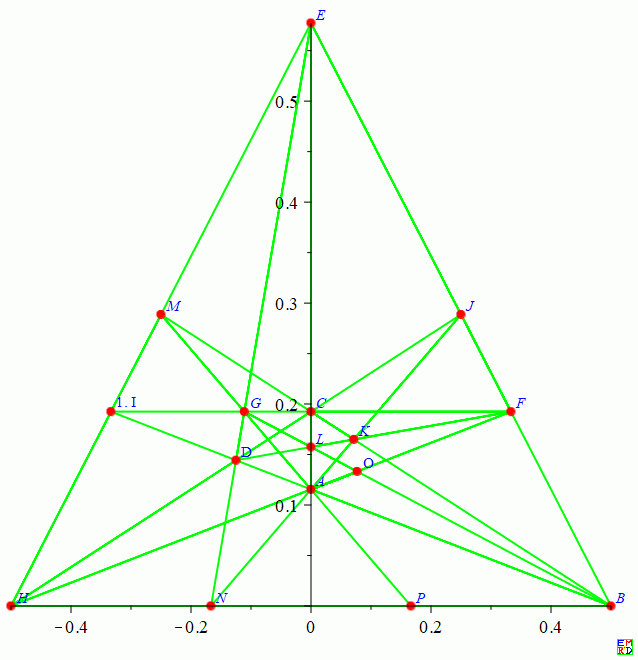
但是上面两个都不是整数解，16棵树整数解最优只有14行，如下图: 1614-3

17棵树

t17
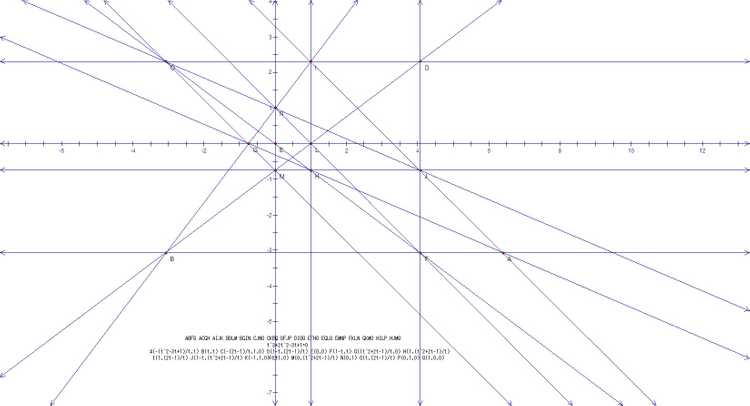
17棵树问题的最优解,这个解无法转化为对称图形，数学星空将其去除无穷远点转化为下图
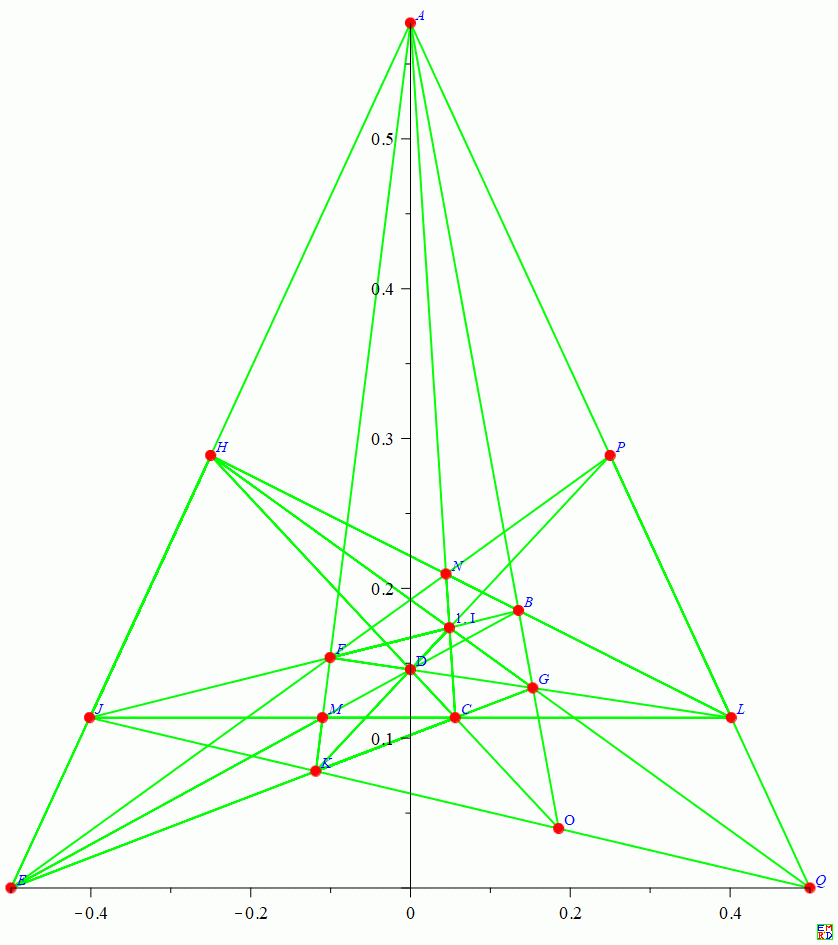
1716-1
而上面结果也不是整数解，17棵树最优整数解只有15行
1715-3
s17.1
s17.2

通过进一步找到了一种更快速的部分判断识别一个点线关系是否存在合法的果树问题解的算法，再次解决了18棵树和19棵树问题。

18棵树

t18
18棵树问题的最优解,以及另外一种对称图 :
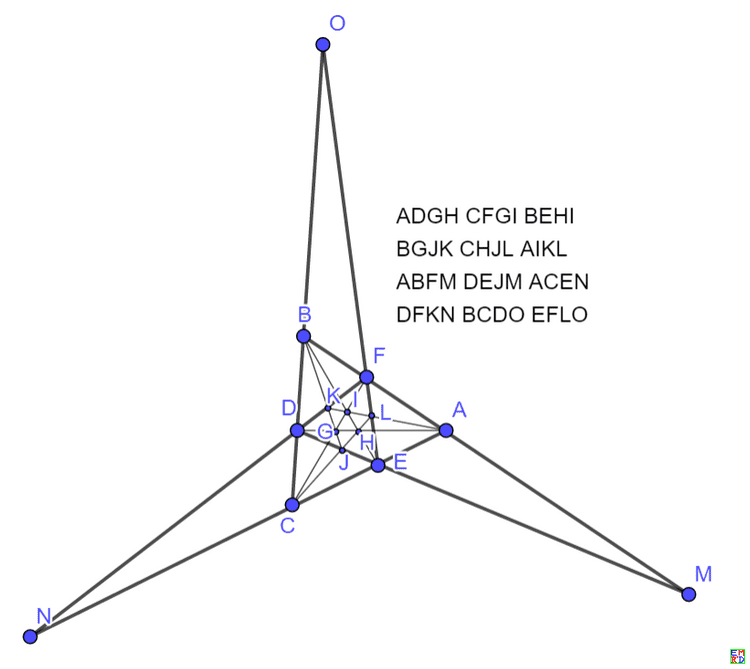
AEHIABGKCEGLCDKMBDFNBCHOEFJOADLOBJLPAFMPCINPDGIQHJMQEKNQFGHRIJKRLMNROPQR
t18r18.4
s18
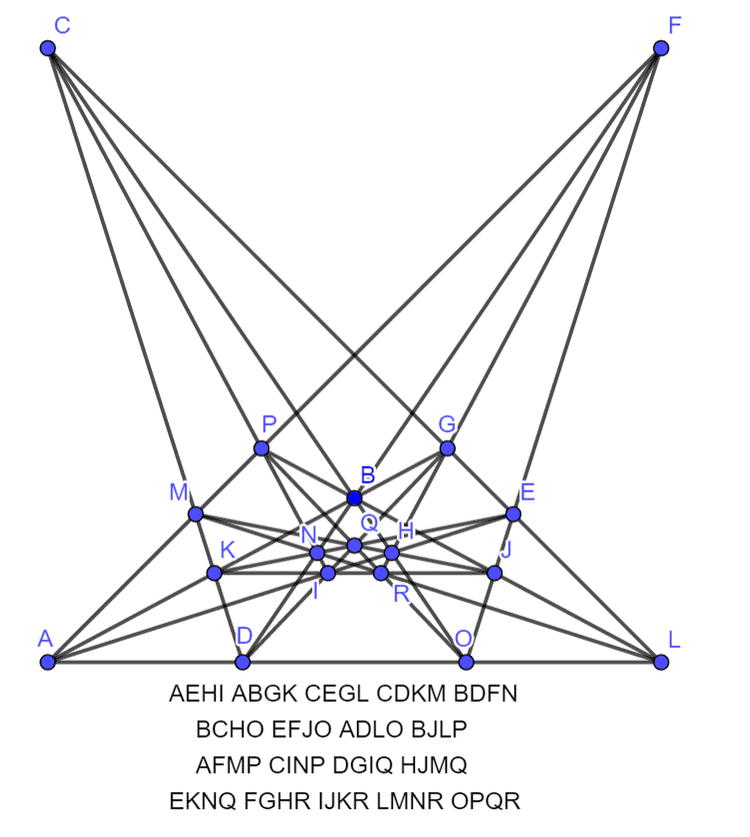
还可以映射为分别包含两个和三个无穷远点的对称图:
s18.3
s18.4

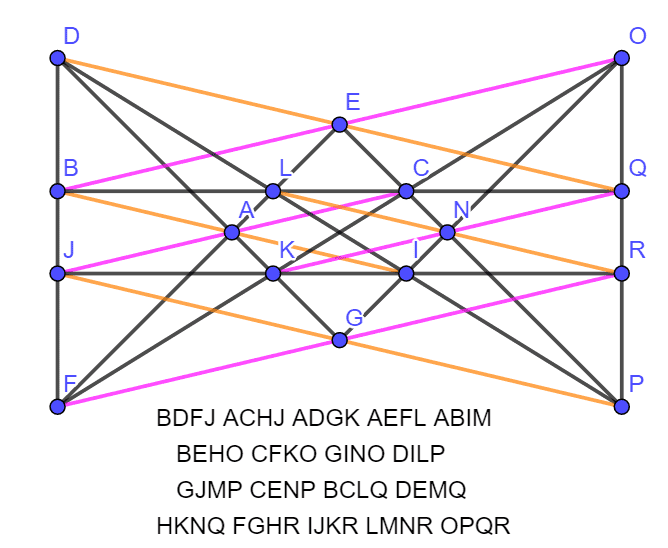
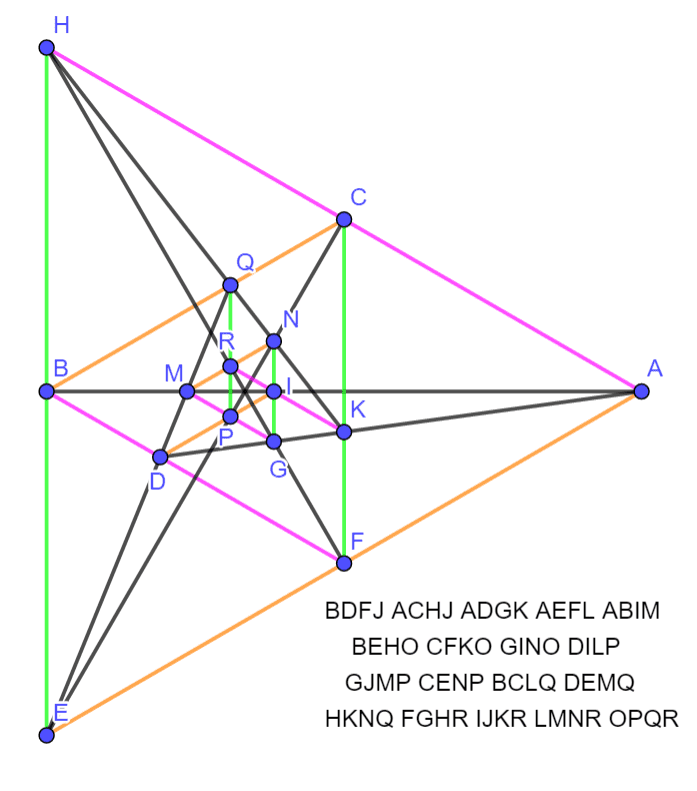
18棵整数解只有17行
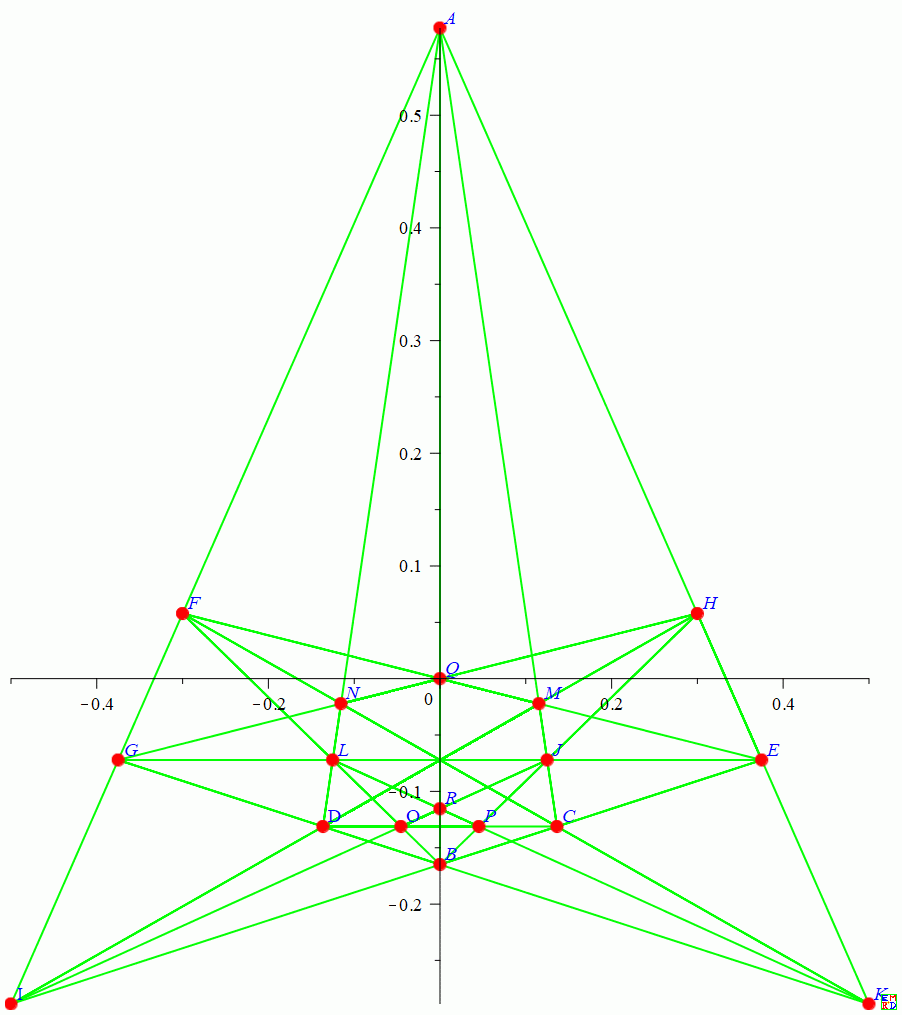
1817-1

19棵树

t19
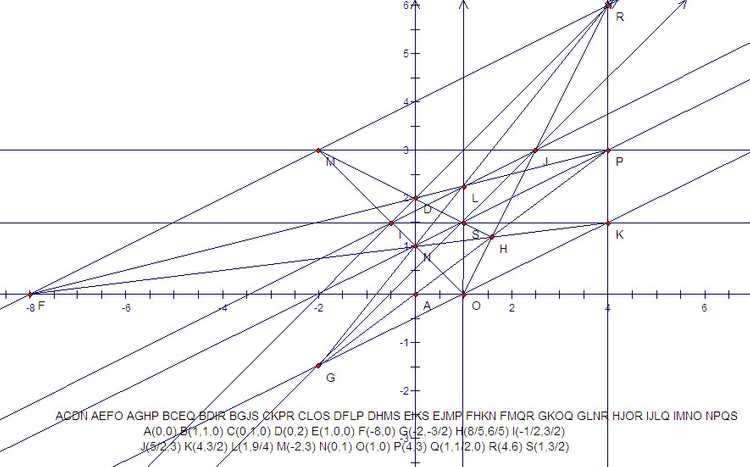
19棵树问题最优解,还可以有下面对称的结构
t19.5
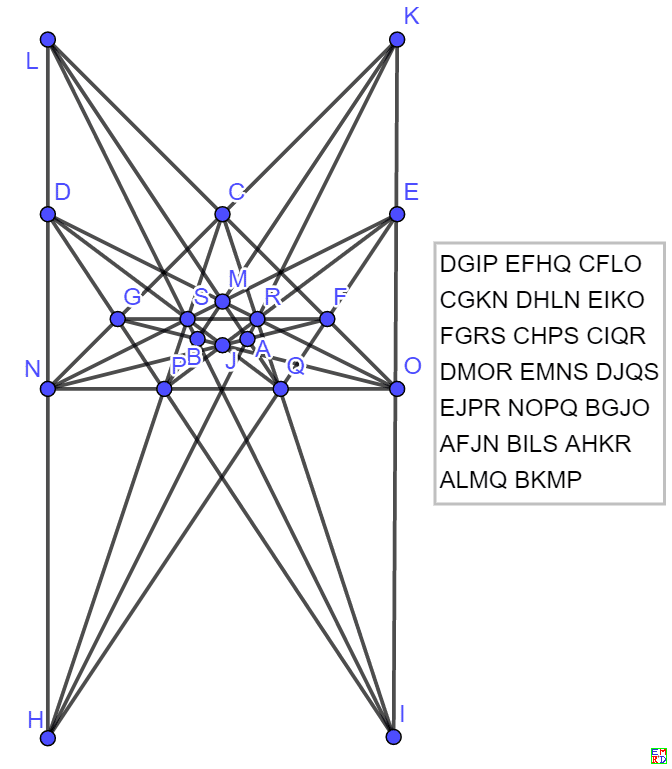
而19棵树20行还有如下整数解

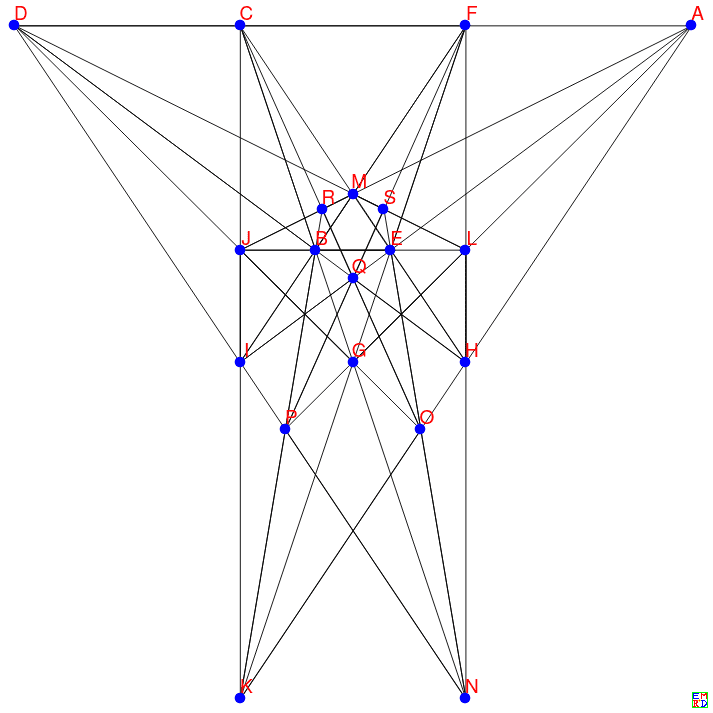
还可以转化为等价的
1920-1
1920-2
1920-3

2009年底，数学研发论坛上的网友一起合作，利用十余人拥有的计算机资源共同计算，验证了20棵树不存在24行解，从而证明23行已经是最优结果。但是，由于拥有的计算资源还不够，我们还不能找出所有的23行解。
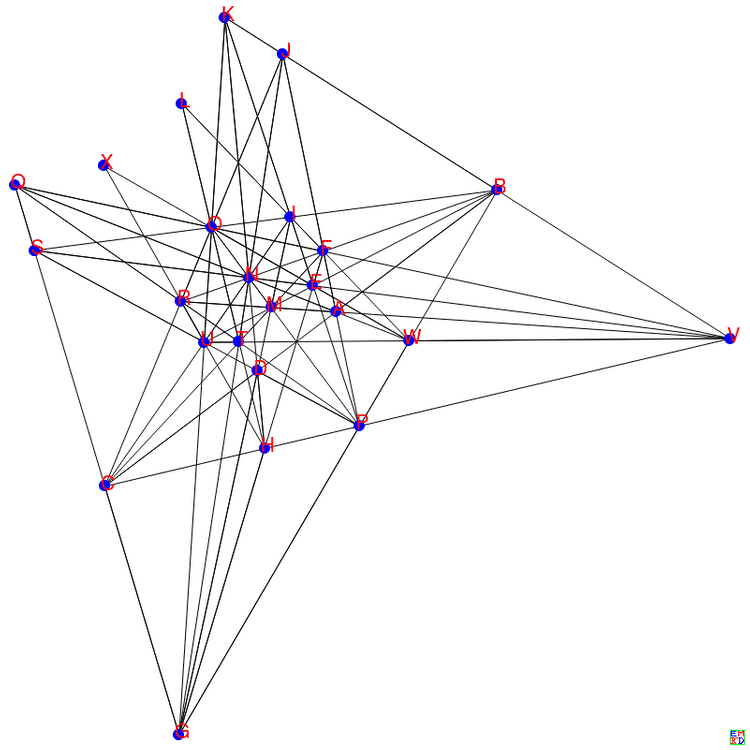
2019年9月，我们重新运行了以前的代码，利用计算机又找出一种和上面两种方案都不等价的新的23行解。

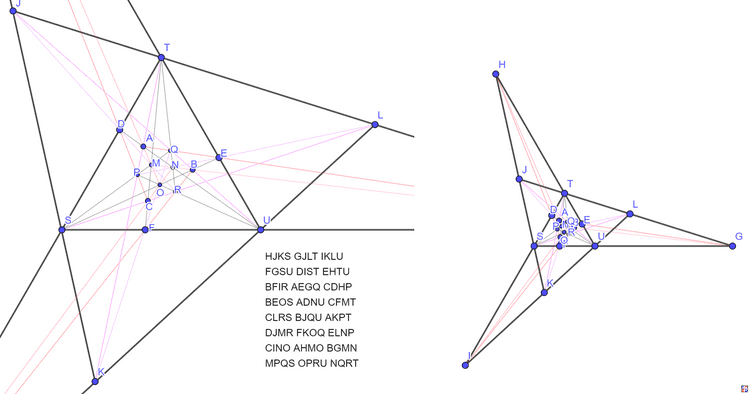
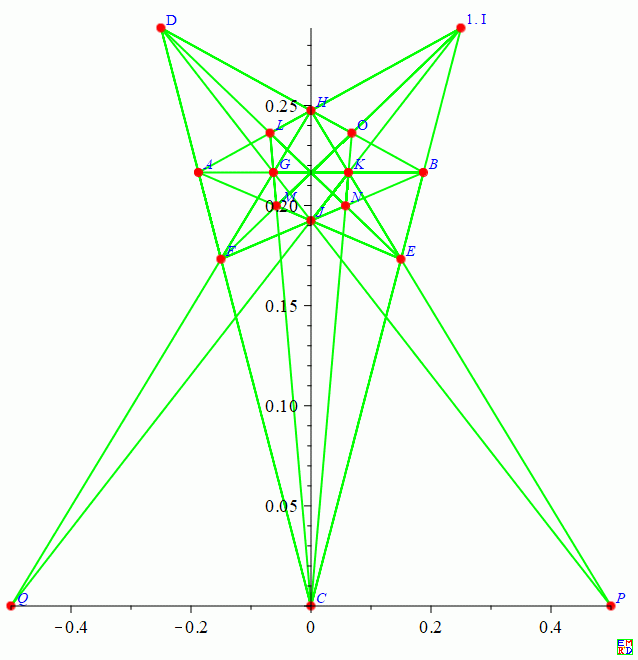
20棵树

这是最后发现的23行图
avatar
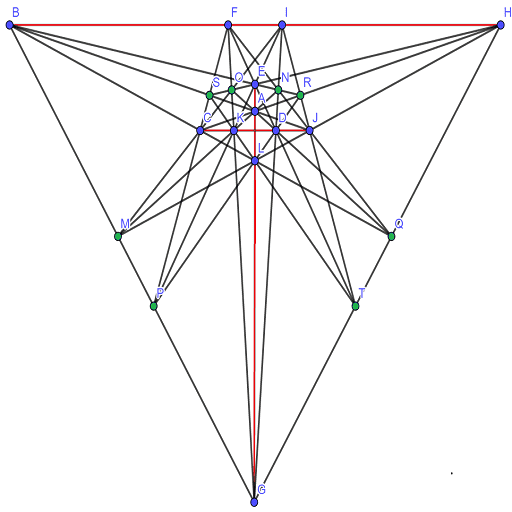
也可以转化为
p20-3
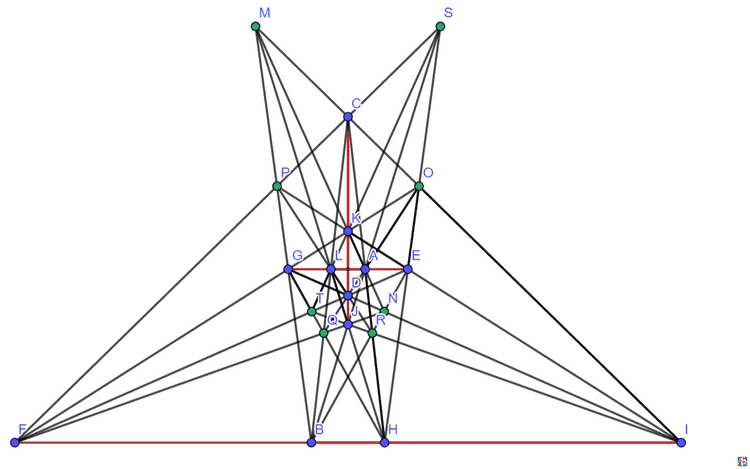
下面是另外两种的不同投影结果

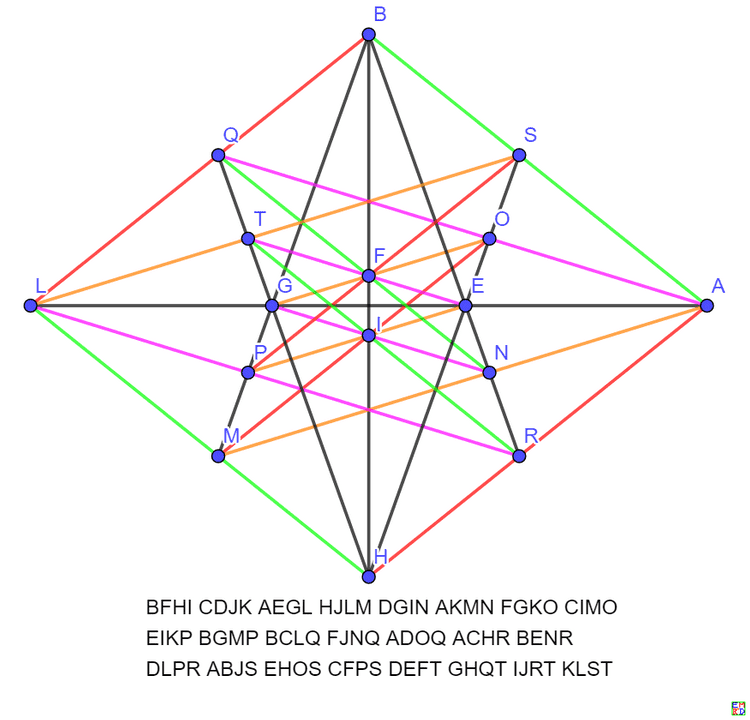
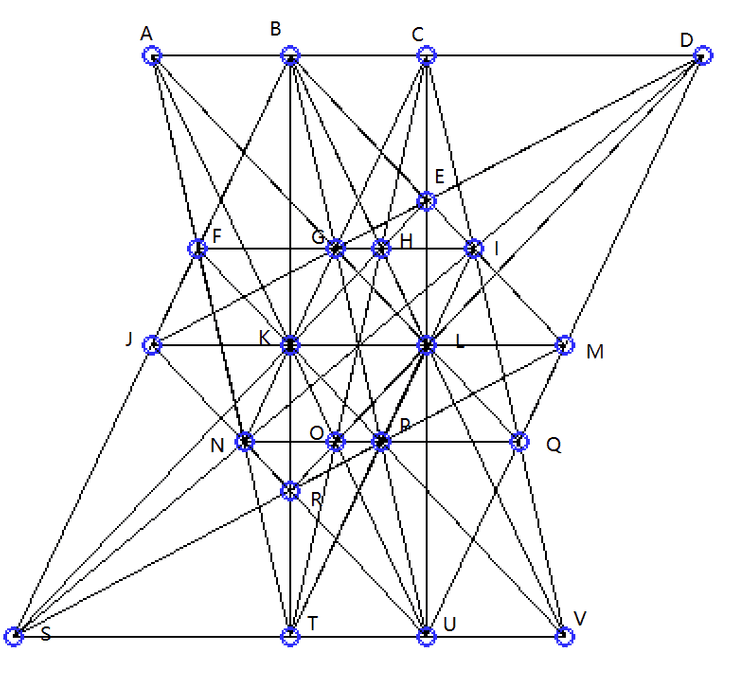
已知的20棵树23行解坐标如下:

解1

print(ADGJBEIJCDHKAFIKCEGLBFHLCJMODINODLMPAHNPGKOPBGMQFJNQAEOQEHMRBKNRCFPRILQRABCSDEFSGHITJKLTMNST);
solve([+1+3\times T_Y+1\times T_Y\times T_Y,-3/5+1\times R_Y-2/5\times T_Y,-4/5+1\times R_X-1/5\times T_Y,-3+1\times H_X-1\times T_Y,-4+1\times P_X-1\times T_Y,+1+1\times S_X,-2+1\times Q_X-1\times T_Y,+2+1\times O_X+1\times T_Y,-1+1\times L_Y-1\times T_Y,+1+1\times P_Y,-3+1\times M_Y-2\times T_Y,+1+1\times D_Y+1\times T_Y,-2+1\times S_Y-1\times T_Y,+1\times G_Y-1\times T_Y,-1+1\times Q_Y,+1+1\times N_Y,-2+1\times C_Y-1\times T_Y,-2+1\times B_Y-1\times T_Y,-1+1\times O_Y,+1+1\times H_Y,+2+1\times C_X+1\times T_Y,-2+1\times N_X-1\times T_Y,-1+1\times L_X,-1+1\times T_X,+2+1\times M_X+1\times T_Y,-2+1\times F_X-1\times T_Y],[T_Y,R_Y,R_X,H_X,P_X,S_X,Q_X,O_X,L_Y,P_Y,M_Y,D_Y,S_Y,G_Y,Q_Y,N_Y,C_Y,B_Y,O_Y,H_Y,C_X,N_X,L_X,T_X,M_X,F_X]);
print("A=[1:0:0] B_x=0 D=[1:D_y:0] E_x=0 E_y=1 F_y=0 G=[1:G_y:0] I_x=0 I_y=0 J=[0:1:0] K_x=1 K_y=0 ");

解2

ACEFDFHJBCIJBEHKADIKBFGMEJLMBDLNCGNODEGPFKNPAJOPAGLQCKMQCHLRDMOREIQRAHNSFIOSBPQSGHITABRTCDST
+4/3+1\times Ey,-1/2+1\times Tx,+3+1\times Py,+2+1\times Qy,-5/2+1\times Qx,+1/2+1\times Rx,-3+1\times Px,+3/2+1\times Lx,-3/2+1\times Mx,-2+1\times Ry,+1+1\times Oy,-2+1\times Ly,+2+1\times My,-3+1\times Nx,+1+1\times Ny,-2+1\times Hy,-1+1\times Ox,-1+1\times Sx,-3+1\times Kx,+1+1\times Ay,+2+1\times Ky,-3/2+1\times Gx,-3/2+1\times Bx,+1+1\times Gy,-1+1\times Ty,-1+1\times Sy
Ey,Tx,Py,Qy,Qx,Rx,Px,Lx,Mx,Ry,Oy,Ly,My,Nx,Ny,Hy,Ox,Sx,Kx,Ay,Ky,Gx,Bx,Gy,Ty,Sy
Ax=1,Az=0,By=0,Bz=1,Cx=1,Cy=0,Cz=0,Dx=0,Dz=1,Dy=1,Dz=1,Ex=1,Ez=0,Fx=0,Fy=1,Fz=0,Hx=0,Hz=1,Ix=1,Iz=1,Iy=0,Iz=1,Jx=0,Jz=1,Jy=0,Jz=1,

解3

print(BFHICDJKAEGLHJLMDGINAKMNFGKOCIMOEIKPBGMPBCLQFJNQADOQACHRBENRDLPRABJSEHOSCFPSDEFTGHQTIJRTKLST);
solve([+1-2\times T_X+1\times P_Y\times T_X-2\times T_X\times T_X,+1\times P_Y-1\times T_X-1\times T_X\times T_X,+1\times P_Y\times P_Y+1\times T_X-3\times P_Y\times T_X,+1\times N_X-1\times P_Y+1\times T_X,-1+1\times P_X+1\times P_Y-1\times T_X,-1+1\times S_X+1\times T_X,-1+1\times S_Y-1\times T_X,+1\times Q_Y+1\times T_X,-2+1\times A_Y+1\times P_Y-1\times T_X,+1+1\times L_Y-1\times P_Y+1\times T_X,+3+1\times F_Y-1\times P_Y+2\times T_X,-1+1\times N_Y+1\times P_Y,-1+1\times K_X+1\times P_Y,+1\times D_X-1\times P_Y,-1+1\times G_Y+1\times P_Y,-1+1\times E_X+1\times T_X,-1+1\times O_X+1\times T_X,-1+1\times B_Y+1\times P_Y-1\times T_X,-1+1\times R_X,-1+1\times A_X,-1+1\times D_Y+1\times P_Y,+1\times G_X-1\times T_X,+1\times Q_X-1\times T_X,-1+1\times R_Y,-1+1\times T_Y,+1\times K_Y-1\times P_Y,+1\times E_Y-1\times P_Y],[P_Y,T_X,N_X,P_X,S_X,S_Y,Q_Y,A_Y,L_Y,F_Y,N_Y,K_X,D_X,G_Y,E_X,O_X,B_Y,R_X,A_X,D_Y,G_X,Q_X,R_Y,T_Y,K_Y,E_Y]);
print("B=[1:B_y:0] C_x=1 C_y=0 F=[1:F_y:0] H=[0:1:0] I=[1:0:0] J_x=0 J_y=1 L_x=0 M_x=0 M_y=0 O_y=0 ");

点击链接可以查看部分关键C++代码。

相关结果被收集到OEIS: A006065 A172992 A172993

理论上下界分析

对于每一棵果树，如果经过这棵果树存在k行，每行4棵，那么这k行除了这棵公共果树，其余果树都互不相同，所以我们得出 $3k\le n-1$ ,n是树的总数。
累加所有果树的结果，这种计数方法将每行都重复统计四次，所以总行数最终不会超过 $\lfloor\frac{(n-1)n}{12}\rfloor$ 。shengjianguo进一步指出，根据单壿著的《组合几何》的结果，可以得出总行数不超过 $\lfloor\frac{(n+2)(n-3)}{14}\rfloor$ 。

射影平面上一条直线方程可以表示为 $ax+by+cz=0$ ,表示其中点[x : y : z] 满足直线[a: b: c]对应的方程。但是反过来，我们也可以把 $ax+by+cz=0$ 看成经过点[a : b: c]的所有直线满足的方程。于是在这种意义下，[x : y : z]需要被看成直线的坐标（或者说对应直线方程的系数），而[a : b: c]被看成一个点。射影几何里面把上述两种看法称为互为对偶。
于是在对偶意义下，一个点被看成直线，直线被看成点；经过一个点的直线被看成一条直线上一点；两条直线的交点被看成过两点的一条直线。
比如20棵树的三个解通过对偶可以分别变化为下面各图:
g1.1
g2.2
g3.5
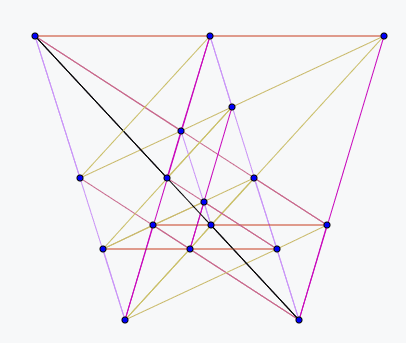
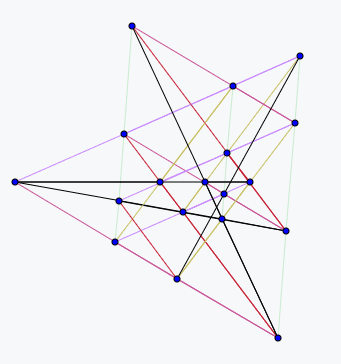
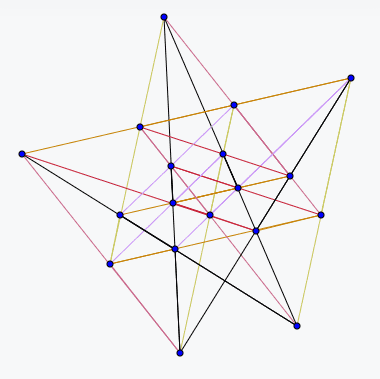
于是果树种植问题的对偶问题就是如何找出n条直线，使得其中正好有k条直线经过的点尽量多。而对于k=4时，如果我们使用 $m\times m$ 的标准网格以及它们构成小正方形中对角线的连线共6m-2条直线，那么除了大正方形四个顶点意外，所有其它交点都正好有四条直线经过。于是我们可以使用6m-2条直线构造出了 $m^2-4$ 个正好4条直线经过的点。由于我们给出了k=4的果树问题的一种下界，不少于 $\frac{n^2}{36}+O(n)$ 。考虑到这种方案中，靠近大正方形四个角的一些斜线经过的点比较少，利用率不高，去除这些斜线可以得出一个八边形模型，可以使用 $14m+O(1)$ 条直线得出 $7m^2+O(m)$ 个四条直线经过的交点，由此我们得出了对于k=4的果树问题的下界不小于 $\frac{n^2}{24}+O(n)$ .
g60

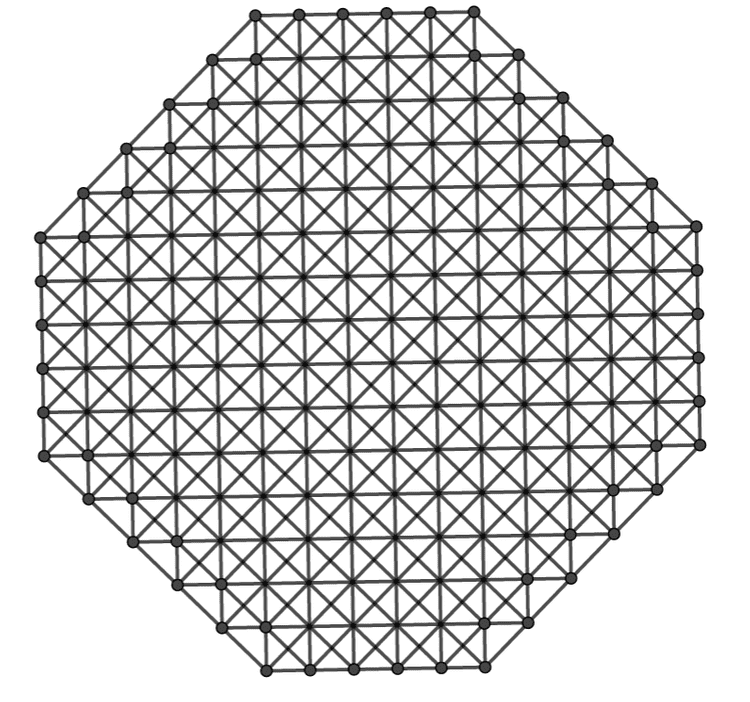
另外根据现在我们已经知道数据，如下面的表格，我们可以猜测k=4的果树问题的数目不小于 $\lfloor\frac{(n-1)(n-3)}{14}\rfloor$ .

n	实数范围A006065	整数范围A172992	复数范围A172993	$\lfloor\frac{(n-1)(n-3)}{14}\rfloor$
4	1	1	1	0
5	1	1	1	0
6	1	1	1	1
7	2	2	2	1
8	2	2	2	2
9	3	3	3	3
10	5	5	5	4
11	6	6	6	5
12	7	7	9	7
13	9	9	9	8
14	10	10	11	10
15	12	12	13	12
16	15	14	15	13
17	16	15	17	16
18	18	17	18	18
19	20	20	20	20
20	23	23	23	23
21	$\ge$ 24	$\ge$ 24	$\ge$ 24	25
22	$\ge$ 28	$\ge$ 26	$\ge$ 28	28
23	$\ge$ 28	$\ge$ 28	$\ge$ 28	31
24	$\ge$ 30	$\ge$ 30	$\ge$ 33	34
25	$\ge$ 32	$\ge$ 32	$\ge$ 35	37

每行四棵最优解完整列表

8棵树以下由于太简单了，这里就不列出了。
下面列表中每三行代表一组解，其中第一行是点线关系，每四个字母代表一行。第二行是一个需要求解的方程组，里面各个用','相隔的表达式都要求等于0。而第三行包含一些已知坐标。比如A=(1,A_y,0) 代表A是一个无穷远点，方向A_y需要从方程组求解。但是如果一个坐标只包含两个数字，那么就认为是普通平面上的一个点，或者说在对应射影平面上z坐标为1. 由于我们的代码还不能完全求解所有方程组，所以列表中可能会包含一些非法情况，比如方程组无解，或解得结果存在五点以上共线的情况等等，需要我们事后再次淘汰。而所有这些解中都把其中某一行果树投影到无穷远直线，如果需要产生果树没有投影到无穷远点的图，需要自己做额外的射影变换。

比如9棵树3行的所有解只有一类，由于含有两个参数，在射影变换等价的意义下有无穷组解

print(ABGHCDGIEFHI);
solve([],[]);
print("A=(1,A_y,0) B=(1,B_y,0) C_x=0 C_y=1 D_x=0 E_x=1 E_y=0 F_y=0 G=(0,1,0) H=(1,0,0) I_x=0 I_y=0 ");

其中第二行全空代表已经没有额外约束条件，所以包含两个自由参数A_y和B_y。

10棵树5行也只有一类，含两个自由参数

print(ABCDAEFGBEHICFHJDGIJ);
solve([+1\times D_Y-1\times D_Y\times I_X-1\times J_Y-1\times D_Y\times J_Y,+1\times G_Y+1\times D_Y\times I_X,-1+1\times J_X+1\times J_Y,+1+1\times C_Y],[D_Y,G_Y,I_X,J_Y,J_X,C_Y]);
print("A=(0,1,0) B=(1,0,0) C=(1,C_y,0) D=(1,D_y,0) E_x=0 E_y=0 F_x=0 F_y=1 G_x=0 H_x=1 H_y=0 I_y=0 ");

从上面方程组我们可以手工解得C_Y = -1, J_X = 1 - J_Y, G_Y = -D_Y\times I_X, D_Y = J_Y / (1 - I_X)

11棵树6行也只有一类，含两个自由参数：

print(ABCJADEKBFGKCHIKDFHJEGIJ);
solve([+1-1\times K_X+1\times I_Y\times K_X,+1\times D_Y-1\times E_Y-1\times D_Y\times K_X,+1\times A_Y+1\times D_Y-1\times E_Y,+1+1\times H_Y-1\times I_Y,-1+1\times I_X,-1+1\times E_X],[D_Y,E_Y,I_Y,K_X,A_Y,H_Y,I_X,E_X]);
print("A_x=0 B_x=0 B_y=0 C_x=0 C_y=1 D=(1,D_y,0) F=(1,0,0) G_x=1 G_y=0 H=(1,H_y,0) J=(0,1,0) K_y=0 ");

12棵树时，开始出现复杂的情况了：
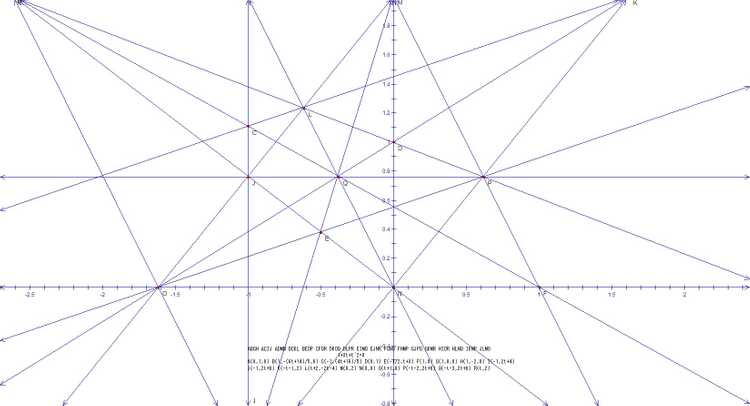
首先，我们原先求得在复数范围中得出两种点线关系不同的8行的情况，不含自由参数

print(ABCDAEFGAHIJBEHKBFILCEJLCGIKDFJKDGHL);
solve([+1-1\times L_X+1\times L_X\times L_X,-1+1\times K_X+1\times L_X,-1+1\times J_Y+1\times L_X,+1\times G_Y-1\times L_X,-1+1\times C_Y+1\times L_X,-1+1\times J_X,-1+1\times I_X,-1+1\times L_Y,+1\times D_Y+1\times L_X,-1+1\times I_Y],[L_X,K_X,J_Y,G_Y,C_Y,J_X,I_X,L_Y,D_Y,I_Y]);
print("A=(0,1,0) B=(1,0,0) C=(1,C_y,0) D=(1,D_y,0) E_x=0 E_y=0 F_x=0 F_y=1 G_x=0 H_x=1 H_y=0 K_y=0 ");

print(AEFGAHIJBEHKBFILCEJLCGIKDFJKDGHL);
solve([+1-1\times L_Y+1\times L_Y\times L_Y,-1+1\times C_Y,+1\times C_X+1\times L_Y,-1+1\times K_Y+1\times L_Y,-1+1\times L_X+1\times L_Y,-1+1\times D_Y,+1+1\times J_Y-1\times L_Y,+1+1\times I_Y,-1+1\times G_X+1\times L_Y,-1+1\times D_X+1\times L_Y],[L_Y,C_Y,C_X,K_Y,L_X,D_Y,J_Y,I_Y,G_X,D_X]);
print("A=(1,0,0) B_x=0 B_y=1 E_x=0 E_y=0 F_x=1 F_y=0 G_y=0 H=(0,1,0) I=(1,I_y,0) J=(1,J_y,0) K_x=0 ");

但是在2019年10月发现在复数范围12棵树可以达到9行，而这个解以前被maxima错误过滤了

        Parameter [+1+1\times t+1\times t^2=0]
        A[0 ,+1 , 0]
        B[+1 ,0 , 0]
        C[+1 ,+1+1\times t , 0]
        D[+1 ,+1\times t , 0]
        E[0 ,0 , +1]
        F[0 ,+1 , +1]
        G[0 ,-1\times t , +1]
        H[+1 ,0 , +1]
        I[+1 ,+1 , +1]
        J[+1 ,+1+1\times t , +1]
        K[+1+1\times t ,0 , +1]
        L[-1\times t ,+1 , +1]
ABCDAEFGAHIJBEHKBFILCEJLCGIKDFJKDGHL

其次在实数或整数范围可以有两种不同点线关系达到7行，分别含有一个和两个自由参数:

print(AHIJBCHKBDILCEJLDGJKEFIKFGHL);
solve([+1\times D_X-1\times K_Y,-1+1\times E_X+1\times K_Y,+1+1\times G_Y-1\times K_Y,+1+1\times J_Y,+1\times F_Y-1\times K_Y,+1\times E_Y-1\times K_Y,-1+1\times F_X,-1+1\times G_X],[D_X,E_X,G_Y,J_Y,F_Y,E_Y,F_X,G_X]);
print("A=(1,A_y,0) B_x=0 B_y=0 C_x=0 C_y=1 D_y=0 H=(0,1,0) I=(1,0,0) J=(1,J_y,0) K_x=0 L_x=1 L_y=0 ");
print(ABIJACDKBEFLCGILDHJLEHIKFGJK);
solve([+1\times F_Y-1\times K_Y+1\times E_X\times K_Y,-1+1\times B_X+1\times F_Y,+1\times F_X+1\times F_Y-1\times K_Y,+1\times G_X-1\times K_Y,+1\times H_Y+1\times K_Y,+1+1\times J_Y,+1\times E_Y-1\times F_Y,+1\times B_Y-1\times F_Y],[E_X,F_Y,K_Y,B_X,F_X,G_X,H_Y,J_Y,E_Y,B_Y]);
print("A_x=0 A_y=1 C_x=0 C_y=0 D=(0,1,0) G_y=0 H=(1,H_y,0) I_x=1 I_y=0 J=(1,J_y,0) K_x=0 L=(1,0,0) ");

13棵树9行还留下不超过6种模式（还需要再验算一下是否每种都是合法的），其中第二种有整数解:

print(ADEFAGHIBDGJBHKLCDKMCEILEHJMFGLMFIJK);
solve([+1+1\times M_Y+1/2\times M_Y\times M_Y,+2+1\times L_Y+2\times M_Y,+1+1\times K_X,-1+1\times L_X-1\times M_Y,+1+1\times B_X+1\times M_Y,+2+1\times C_Y+1\times M_Y,-1+1\times C_X-1\times M_Y,-1+1\times I_X-1\times M_Y,+1\times K_Y+1\times M_Y,+1+1\times H_Y,+1\times I_Y+1\times M_Y,+1\times F_Y+1\times M_Y],[M_Y,L_Y,K_X,L_X,B_X,C_Y,C_X,I_X,K_Y,H_Y,I_Y,F_Y]);
print("A_x=0 A_y=1 B_y=0 D_x=0 D_y=0 E=(0,1,0) F_x=0 G_x=1 G_y=0 H=(1,H_y,0) J=(1,0,0) M=(1,M_y,0) ");
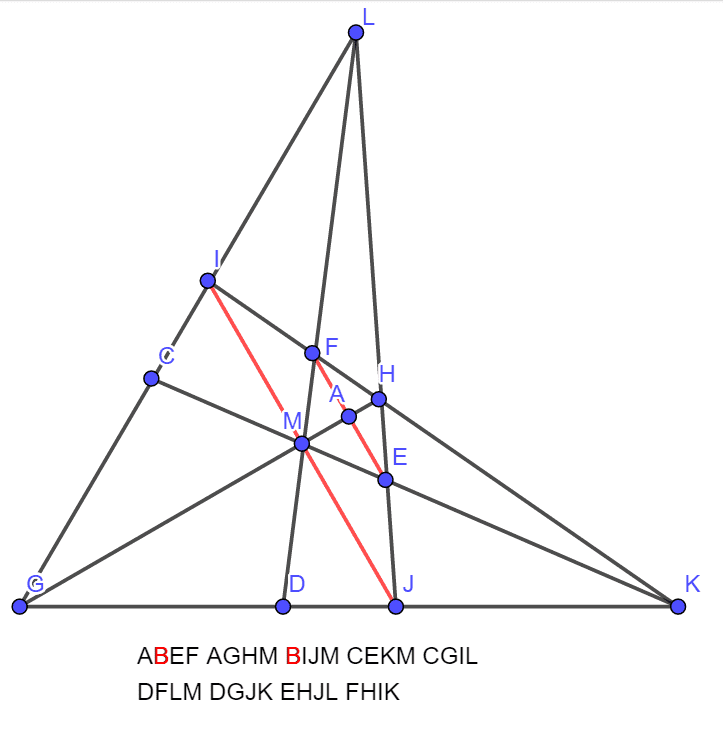
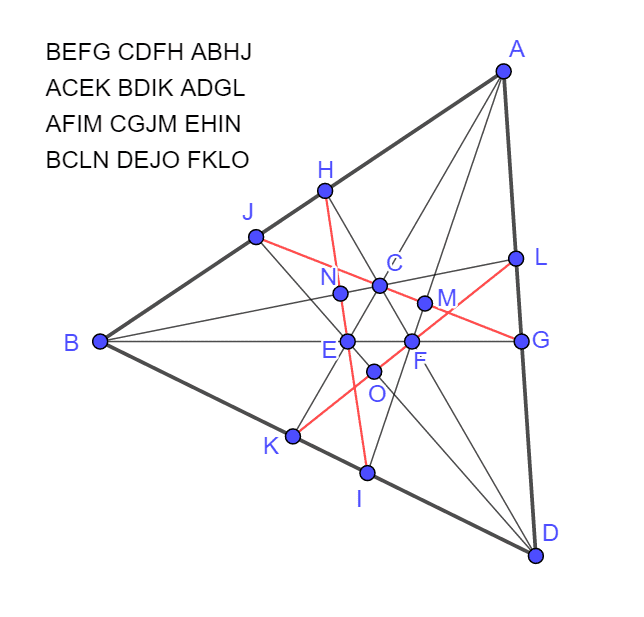
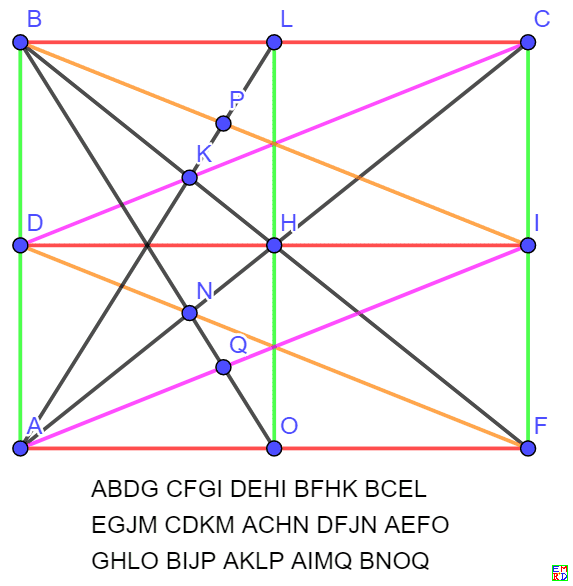
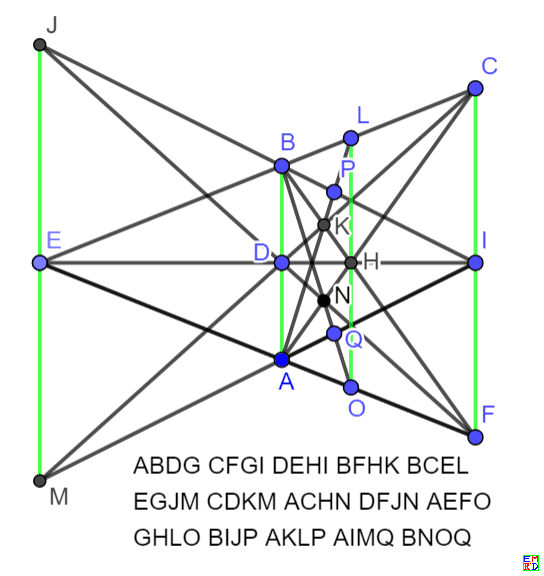
print(ABEFAGHMBIJMCEKMCGILDFLMDGJKEHJLFHIK);
solve([+2+1\times L_Y,+1+1\times L_X,-4+1\times C_Y,-3+1\times G_Y,-2+1\times K_Y,+4+1\times D_Y,+1+1\times J_Y,-1+1\times K_X,-1+1\times H_Y,-1+1\times C_X,+1+1\times D_X,+1+1\times F_X],[L_Y,L_X,C_Y,G_Y,K_Y,D_Y,J_Y,K_X,H_Y,C_X,D_X,F_X]);
print("A=(1,0,0) B_x=0 B_y=0 E_x=1 E_y=0 F_y=0 G=(1,G_y,0) H=(1,H_y,0) I_x=0 I_y=1 J_x=0 M=(0,1,0) ");
print(BCDEBFGHBIJKCFILCGJMDFKMDHJLEGKLEHIM);
solve([+1-1\times M_X+1\times M_X\times M_X,-1+1\times L_X+1\times M_X,-1+1\times K_Y+1\times M_X,+1\times H_Y-1\times M_X,-1+1\times D_Y+1\times M_X,-1+1\times K_X,-1+1\times J_X,-1+1\times M_Y,+1\times E_Y+1\times M_X,-1+1\times J_Y],[M_X,L_X,K_Y,H_Y,D_Y,K_X,J_X,M_Y,E_Y,J_Y]);
print("B=(0,1,0) C=(1,0,0) D=(1,D_y,0) E=(1,E_y,0) F_x=0 F_y=0 G_x=0 G_y=1 H_x=0 I_x=1 I_y=0 L_y=0 ");
print(AEFGAHIMBEHJBFKMCELMCGIKDGJMDHKLFIJL);
solve([+1+1\times L_Y-1\times L_Y\times L_Y,+1+1\times D_Y-1\times L_Y,-1+1\times C_Y-1\times L_Y,+2+1\times H_Y-1\times L_Y,+1+1\times J_Y,-1+1\times B_Y+1\times L_Y,+1\times L_X+1\times L_Y,-1+1\times J_X,+1\times E_X+1\times L_Y,+1\times C_X+1\times L_Y,-1+1\times D_X,+1+1\times I_Y],[L_Y,D_Y,C_Y,H_Y,J_Y,B_Y,L_X,J_X,E_X,C_X,D_X,I_Y]);
print("A=(1,0,0) B_x=0 E_y=0 F_x=0 F_y=0 G_x=1 G_y=0 H=(1,H_y,0) I=(1,I_y,0) K_x=0 K_y=1 M=(0,1,0) ");
print(ABLMAFGHBIJKCFILCGJMDFKMDHJLEGKLEHIM);
solve([+1+1\times M_Y+1\times M_Y\times M_Y,+1+1\times K_X+1\times M_Y,+1/3+1\times B_Y-1/3\times M_Y,+1+1\times D_X,+1\times E_X+1\times M_Y,+1\times J_X-1\times M_Y,-1+1\times C_X-1\times M_Y,+1\times D_Y+1\times M_Y,-1+1\times E_Y,-1+1\times K_Y,+1\times J_Y+1\times M_Y,+1\times H_Y+1\times M_Y],[M_Y,K_X,B_Y,D_X,E_X,J_X,C_X,D_Y,E_Y,K_Y,J_Y,H_Y]);
print("A=(0,1,0) B=(1,B_y,0) C_y=0 F_x=0 F_y=0 G_x=0 G_y=1 H_x=0 I_x=1 I_y=0 L=(1,0,0) M=(1,M_y,0) ");
print(ABKLAGHMBIJMCDKMCGILDHJLEFLMEHIKFGJK);
solve([+1-1\times K_X\times K_X,-1+1\times F_Y+1\times K_X,-1+1\times D_Y+1\times K_X,+1+1\times E_Y-1\times K_X,+1+1\times C_Y-1\times K_X,+1\times I_Y-1\times K_X,-1+1\times E_X,-1+1\times F_X,+1\times G_Y+1\times K_X,+1\times C_X-1\times K_X,+1+1\times H_Y,+1\times D_X-1\times K_X],[K_X,F_Y,D_Y,E_Y,C_Y,I_Y,E_X,F_X,G_Y,C_X,H_Y,D_X]);
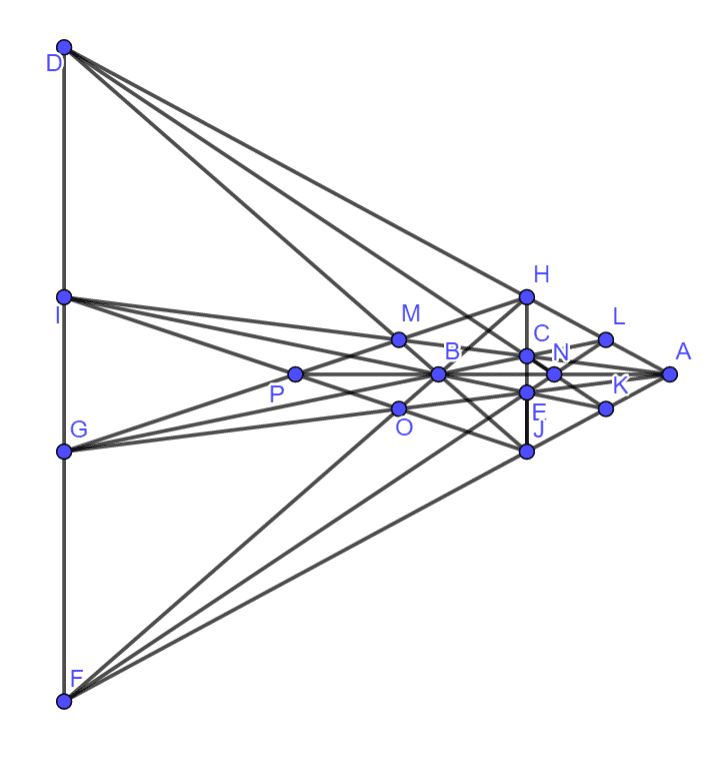
print("A=(1,0,0) B_x=0 B_y=0 G=(1,G_y,0) H=(1,H_y,0) I_x=0 J_x=0 J_y=1 K_y=0 L_x=1 L_y=0 M=(0,1,0) ");

14棵以上候选解太多了，如有需要请下载：

所有数据openf4 有限域处理结果click to download all best result candidates from 12 to 18 trees

其它优秀解

24棵复数解

2019年11月29日发现24棵33行的复数解:

print(ABGIAFHLBCHJCDIKDEJLEFGKAMOSBNPTCOQUDPRVEMQWFNRXAKRTBLMUCGNVDHOWEIPXFJQSGRSUHMTVINUWJOVXKPSWLQTXGJMPHKNQILORACWXAEUVBDSXBFVWCESTDFTU);
solve([+1-3\times X_Y+3\times X_Y\times X_Y,+2/7+1\times Q_Y-12/7\times X_Y,+1\times J_X-2\times X_Y,-8/7+1\times Q_X+6/7\times X_Y,-2/3+1\times S_X,-1/2+1\times R_Y-1/2\times X_Y,-1+1\times V_X+1\times X_Y,+1\times T_Y-3/2\times X_Y,+1\times D_X-1\times X_Y,-3/2+1\times N_X+3/2\times X_Y,-1/2+1\times P_X-1/2\times X_Y,+1\times U_Y-2\times X_Y,+3+1\times G_Y-3\times X_Y,+1/2+1\times K_Y-3/2\times X_Y,-1+1\times I_Y+3\times X_Y,-1/2+1\times T_X,-2/3+1\times O_Y,+1+1\times E_Y-3\times X_Y,-2/3+1\times O_X,+1\times M_Y-2\times X_Y,+1\times P_Y-3/2\times X_Y,-2/3+1\times M_X,-1+1\times W_X,-1+1\times X_X,-1+1\times U_X+1\times X_Y,-1+1\times E_X+1\times X_Y,+1\times D_Y-1\times X_Y,+1\times S_Y-1\times X_Y,-1+1\times W_Y,-1+1\times V_Y,+1\times N_Y-3/2\times X_Y,+1\times L_Y-2\times X_Y,-1/2+1\times R_X,-1/2+1\times K_X],[X_Y,Q_Y,J_X,Q_X,S_X,R_Y,V_X,T_Y,D_X,N_X,P_X,U_Y,G_Y,K_Y,I_Y,T_X,O_Y,E_Y,O_X,M_Y,P_Y,M_X,W_X,X_X,U_X,E_X,D_Y,S_Y,W_Y,V_Y,N_Y,L_Y,R_X,K_X]);
print("A=(0,1,0) B=(1,0,0) C_x=1 C_y=0 F_x=0 F_y=1 G=(1,G_y,0) H_x=0 H_y=0 I=(1,I_y,0) J_y=0 L_x=0 ");

26棵复数解

26棵树35行的复数解:

        Parameter [+1-1\times t+2\times t^2-2\times t^3+1\times t^4=0]                                                                                                   A[+1 ,0 , +1]
        B[+1\times t ,-1\times t , +1]
        C[-1\times t^3 ,+1+1\times t^2+1\times t^3 , +1]
        D[+1-1\times t+1\times t^2-1\times t^3 ,+1+1\times t^3 , +1]
        E[+1 ,+1\times t-1\times t^2+1\times t^3 , +1]
        F[+1\times t ,0 , +1]
        G[-1\times t^3 ,+1\times t^3 , +1]
        H[+1-1\times t+1\times t^2-1\times t^3 ,+1\times t^3 , +1]
        I[+1 ,-1\times t^2+1\times t^3 , +1]
        J[+1\times t ,-1\times t^2+1\times t^3 , +1]
        K[-1\times t^3 ,+1+1\times t^2 , +1]
        L[+1-1\times t+1\times t^2-1\times t^3 ,+1\times t-1\times t^2+1\times t^3 , +1]
        M[+1 ,-1+1\times t-1\times t^2+1\times t^3 , 0]
        N[0 ,+1 , +1]
        O[+1\times t^2-1\times t^3 ,+1-1\times t+1\times t^2 , +1]
        P[+1\times t-1\times t^2 ,+1\times t^2 , +1]
        Q[+1 ,-1+1\times t-2\times t^2+1\times t^3 , 0]
        R[0 ,+1-1\times t+1\times t^2 , +1]
        S[+1\times t^2-1\times t^3 ,+1\times t^3 , +1]
        T[+1\times t-1\times t^2 ,+1\times t-1\times t^2+1\times t^3 , +1]
        U[+1 ,0 , 0]
        V[0 ,0 , +1]
        W[+1\times t^2-1\times t^3 ,-1\times t^2+1\times t^3 , +1]
        X[+1\times t-1\times t^2 ,+1-1\times t+1\times t^2 , +1]
        Y[0 ,+1 , 0]
AEIYBFJYCGKYDHLYMQUYNRVYOSWYPTXYABMOALNXBCNPCDOQDEPREFQSFGRTGHSUHITVIJUWJKVXKLMWAFUVAHPQBGVWBIQRCHWXCJRSDIMXDKSTEJMNELTUFKNOGLOPMPSVNQTWORUX

21棵整数解

21棵树24行整数解例子:
o21.2

	A(1/4,+1)
        B(+1,2/3)
        C(3/2,4)
        D(+0,+1)
        E(+1,+0)
        F[+1,8/3,0];
        G[+1,-4/3,0];
        H(-1/2,+0)
        I(+0,-2)
        J(-1/2,2/3)
        K(-1/2,-2)
        L(3/2,-2)
        M(1/2,4/3)
        N(3/4,+1)
        O(+1,2)
        P(1/2,2)
        Q(1/2,2/3)
        R(3/2,2)
        S[+0,+1,0];
        T(+0,+0)
        U[+1,+0,0];
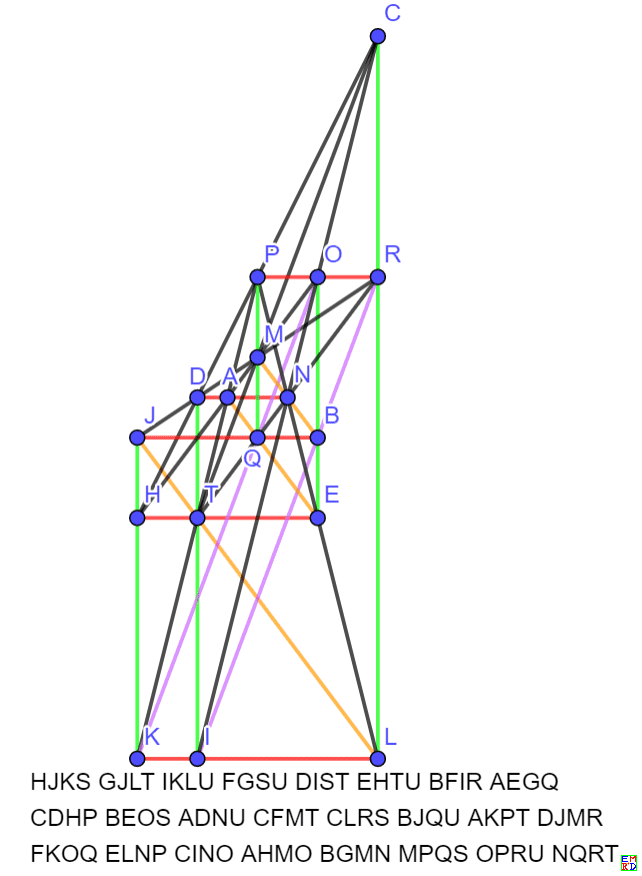
HJKSGJLTIKLUFGSUDISTEHTUBFIRAEGQCDHPBEOSADNUCFMTCLRSBJQUAKPTDJMRFKOQELNPCINOAHMOBGMNMPQSOPRUNQRT

22棵整数解

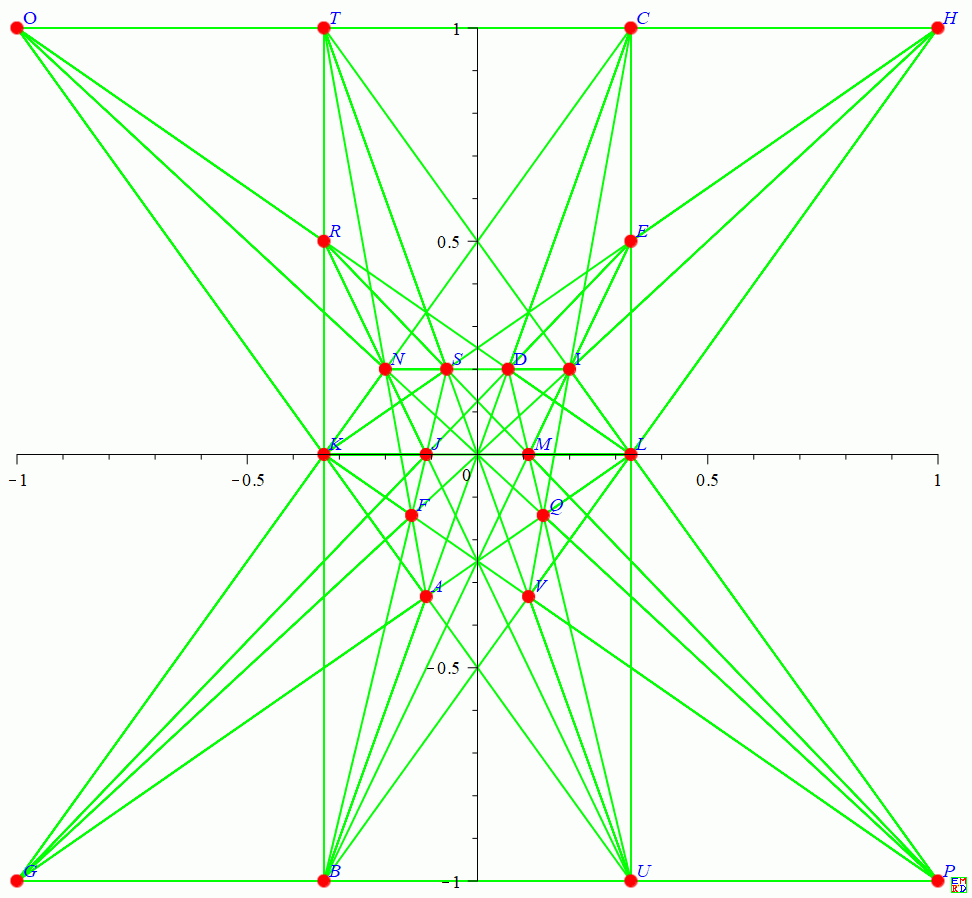
转载自efriedma 网站的22棵26行,23棵28行，24棵30行，25棵32行整数解 s22
(需要注意下面数据对上图做了额外的射影变换，和上图中点的坐标不匹配。下面数据将AKOU映射为无穷远直线）

        A[+1,1/3,0];
        B(+0,+0)
        C(+1,1/3)
        D(3/2,1/2)
        E(4/3,1/3)
        F(4,2)
        G(+1,+0)
        H(4/3,2/9)
        I(8/5,2/5)
        J(2,+1)
        K[+0,+1,0];
        L(2,1/3)
        M(2,1/2)
        N(+1,+1)
        O[+1,-1/3,0];
        P(4,+0)
        Q(5/2,1/2)
        R(+0,+1)
        S(4/3,2/3)
        T(+0,2/3)
        U[+1,+0,0];
        V(4,2/3)
ABCDAGLQAKOUAFNTBFJSBKRTBGPUBHLVBEIMCGKNCHOTCELUCIQVDEGJDINSDLORDMQUEHKSFGHIFKPVILPTJKLMJNRUMPRSNOPQSTUV

数学星空后来再次将它转化为如下对称结构：
2226

23棵整数解

23棵28行整数解
t23

       A(+0,+0)
        B(1/3,+1)
        C(1/2,3/2)
        D(5/6,5/2)
        E(-1/6,1/2)
        F(+0,+1)
        G(1/3,2)
        H(1/2,5/2)
        I(-1/6,3/2)
        J(+0,2)
        K(-1/6,5/2)
        L(-1,4)
        M[+1,1,0];
        N[+1,+0,0];
        O[+1,-1,0];
        P[+0,+1,0];
        Q(+1,+0)
        R(+1,+1)
        S(5/6,1/2)
        T(+1,2)
        U(5/6,3/2)
        V(1/2,1/2)
        W(1/3,+0)

24棵整数解

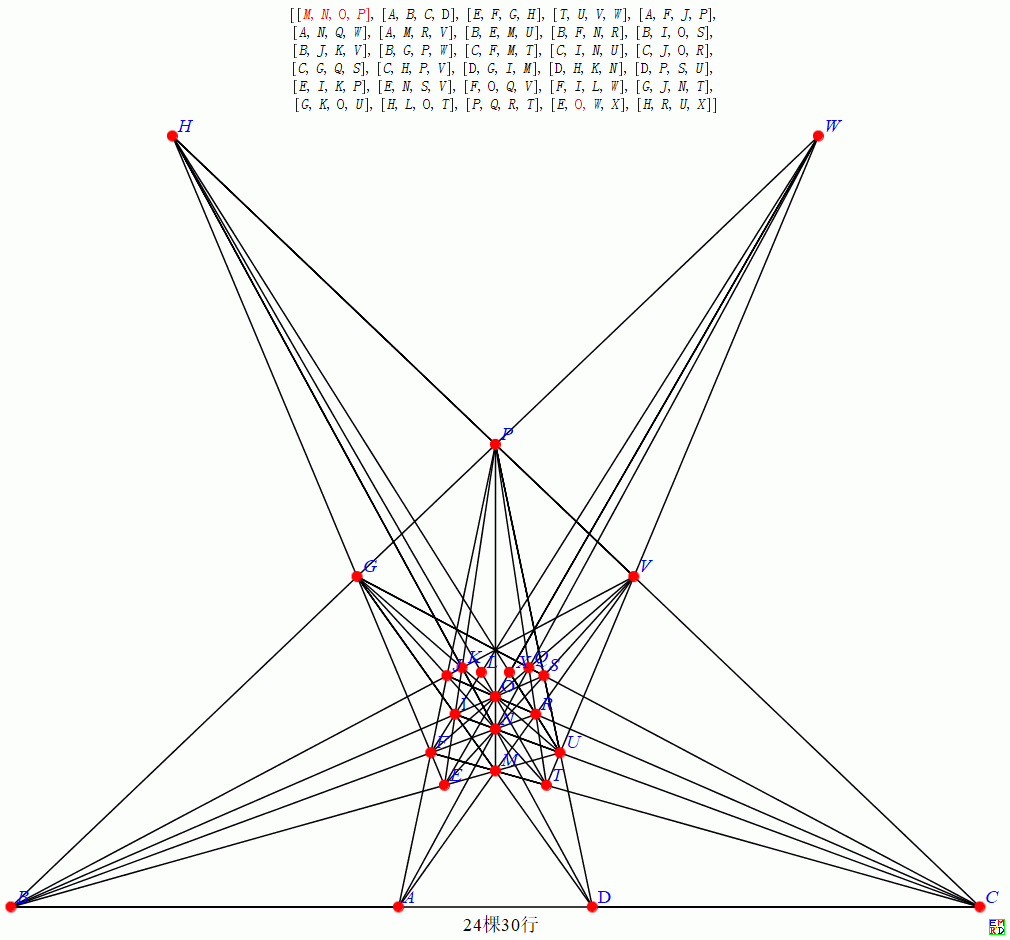
24棵30行整数解
t24.30
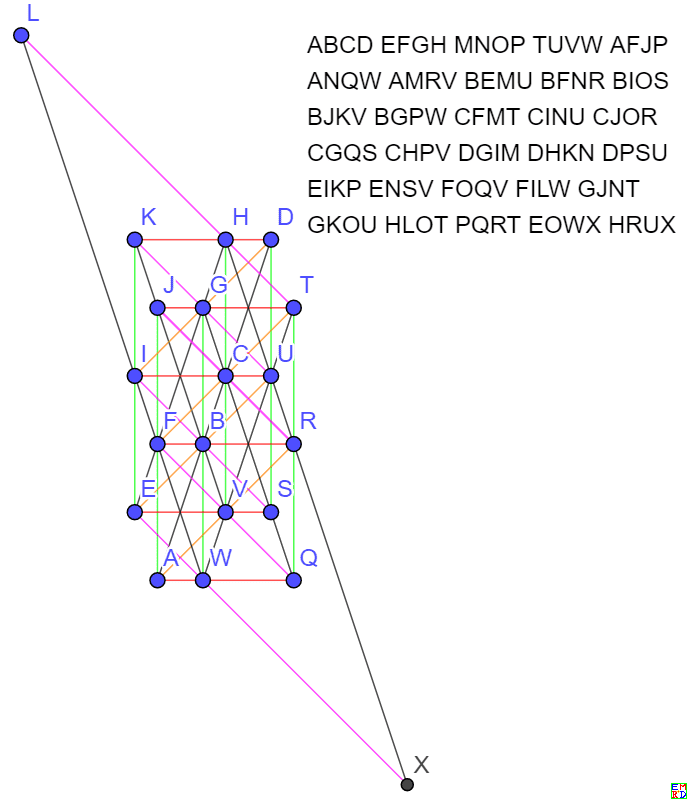
或者左右对称图
s24
和数学星空的对称结构
J2430-1
坐标同23棵28行整数解

25棵整数解

25棵32行整数解
t25

       A(+1,3/2)
        B[+0,+1,0];
        C(+1,+0)
        D(+1,2/3)
        E(3/2,2)
        F[+1,2,0];
        G(3/4,1/2)
        H(5/6,2/3)
        I(+0,+0)
        J(1/2,1/2)
        K(1/2,2/3)
        L(5/12,5/6)
        M(3/2,+1)
        N[+1,+0,0];
        O(+0,+1)
        P(3/4,+1)
        Q(3/10,6/5)
        R(5/16,5/4)
        S(1/4,3/2)
        T[+1,-1,0];
        U(+0,2)
        V(5/4,1/2)
        W(3/2,+0)
        X(1/2,2)
        Y(3/4,3/2)

随着树的数目增加，我们越来越难以穷举所有的情况。于是我们开始结合群论知识，使用开源nauty代码，仅搜索具有高度自同构结构的结果，从而找出几个高度对称的结果：

22棵实数解

2019年12月6日发现22棵28行实数解
o22

        [+1\times t^3+6\times t^2+5\times t+1]
        A[+1,+0,0];
        B[+1,1\times t-2\times (1\times t^2+6\times t+3)+2,0];
        C[+1,+1,0];
        D(-1\times (1\times t^2+6\times t+3),-1\times t+2\times (1\times t^2+6\times t+3))
        E(+1,-1\times (1\times t^2+6\times t+3))
        F(1\times t-1\times (1\times t^2+6\times t+3)+1,1\times t+1)
        G(-t,-2\times t+1\times (1\times t^2+6\times t+3)-1)
        H(-t,-t)
        I(1\times t-1\times (1\times t^2+6\times t+3)+1,(1\times t^2+6\times t+3))
        J(-1\times (1\times t^2+6\times t+3)+1,-1\times t+1\times (1\times t^2+6\times t+3)-1)
        K(+0,+1)
        L(+1,+0)
        M(-1\times (1\times t^2+6\times t+3),-1\times t+1\times (1\times t^2+6\times t+3))
        N(-1\times (1\times t^2+6\times t+3)+1,-1\times t+1\times (1\times t^2+6\times t+3))
        O(+0,+0)
        P(-t,-1\times t+1\times (1\times t^2+6\times t+3))
        Q(1\times t-1\times (1\times t^2+6\times t+3)+1,+0)
        R(+1,+1)
        S(-1\times (1\times t^2+6\times t+3),-1\times t+1\times (1\times t^2+6\times t+3)-1)
        T(-1\times (1\times t^2+6\times t+3)+1,+1)
        U(+0,-1\times t+1\times (1\times t^2+6\times t+3)-1)
        V[+0,+1,0];
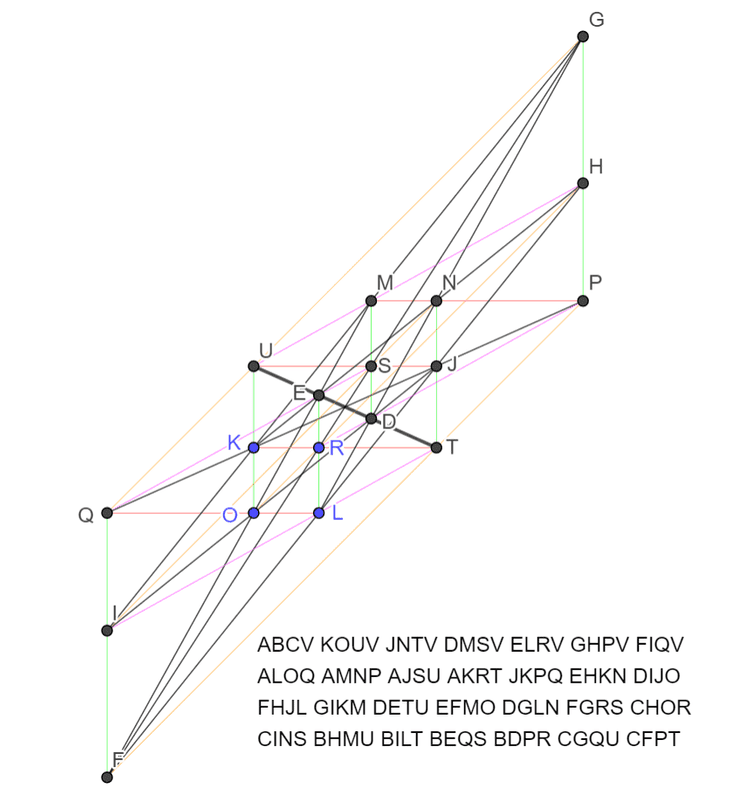
ABCVKOUVJNTVDMSVELRVGHPVFIQVALOQAMNPAJSUAKRTJKPQEHKNDIJOFHJLGIKMDETUEFMODGLNFGRSCHORCINSBHMUBILTBEQSBDPRCGQUCFPT

wayne对这个图进行射影变换后我们发现图形很像正七边形，于是我们手工制作了对应的七个方向对称的正七边形图 : w22.7

25棵复数解

2019年12月10日发现25棵35行复数解

        [+1\times t^4+4\times t^3+8\times t^2+5\times t+1]
        A(-2\times t^3 - 7\times t^2 - 12\times t - 3,t^3 + 4\times t^2 + 7\times t + 3)
        B(-2\times t^3 - 7\times t^2 - 12\times t - 4,t^2 + t + 1)
        C(-t^3 - 4\times t^2 - 8\times t - 3,-t^3 - 4\times t^2 - 6\times t - 1)
        D(-2\times t^3 - 7\times t^2 - 12\times t - 4,-t)
        E(+1,+0)
        F(+1, -t^3 - 4\times t^2 - 7\times t - 2)
        G(-t^3 - 4\times t^2 - 8\times t - 3, -t^3 - 4\times t^2 - 7\times t - 2)
        H(+1,t+1)
        I(-2\times t^3 - 7\times t^2 - 12\times t - 3,+0)
        J(-t^3 - 4\times t^2 - 8\times t - 3,t+1)
        K(-2\times t^3 - 7\times t^2 - 12\times t - 3, -t^3 - 3\times t^2 - 5\times t - 1)
        L(-2\times t^3 - 7\times t^2 - 12\times t - 4, -t^3 - 3\times t^2 - 5\times t - 1)
        M[+1,+0,0];
        N(-3\times t^3 - 11\times t^2 - 20\times t - 7,+1)
        O(-2\times t^3-7\times t^2-13\times t-4,+1)
        P(+0,+1)
        Q[+1,t^3 + 3\times t^2 + 6\times t + 2,0];
        R[+1,t,0];
        S(-2\times t^3-7\times t^2-13\times t-4,1\times t^3+3\times t^2+5\times t+2)
        T(+0,-2\times t^3-7\times t^2-13\times t-4)
        U(+0,+0)
        V(-3\times t^3 - 11\times t^2 - 20\times t - 7,t+1)
        W(-2\times t^3-7\times t^2-13\times t-4, -t^3 - 4\times t^2 - 7\times t - 2)
        X(-3\times t^3 - 11\times t^2 - 20\times t - 7, -t^3 - 3\times t^2 - 5\times t - 1)
        Y[+0,+1,0];
EFHYCGJYAIKYBDLYMQRYPTUYNVXYOSWYFGMWKLMXHJMVEIMUHKUWCLVWBCSTADUXEJRSFKQTEGQXDIRVILNTFIPSGLOUAEOTBKPVDJPWBJOXDGNSAHPRCFNRCHOQABNQMNOPRTWXQSUV

通过利用自同构群的结构，我们还可以用来判断一个图是否存在对称做法，并且找出对应的对称方案 :

24棵对称解

24棵树30行的两个高度对称图
IOPULNOXJQRVKMRTHNQWGMPSKLUVGHTXIJSWAGKOBHLRFILQDGINCHJMEJKPAJTUBIVXFGUWCLTWDKSXEHSVARWXBOSTEQUXDMVWFPTVCNSUABMNEFORCDPQ
$\frac{UA}{UT}=0.5048, \frac{UJ}{UT}=0.4378$
o24.4

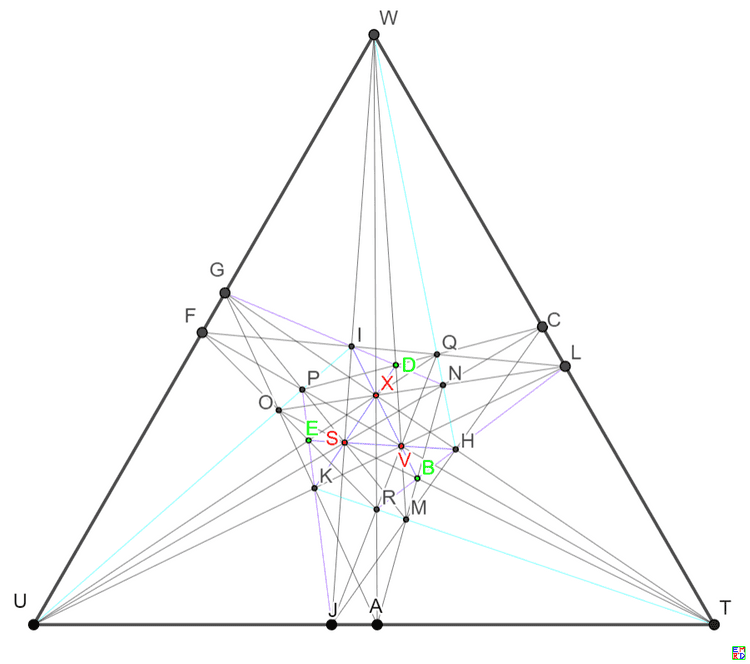
AJPWAIQVAHRXFGUVEFSXEGTWDKPTCKQUBKRSBDNVCDMXBCOWFLOPGLMRELNQHIOTHJNUIJMSAMNOLSTUKVWXIPUXJRTVHQSWCNPSDORUBMQTEMPVGOQXFNRW
$t^3-t^2-2t+1=0$ , $t=0.44504186791262880857780512899358951893$
$\frac{VA}{AQ}=1-t, \frac{VF}{FU}=t$
o24.5

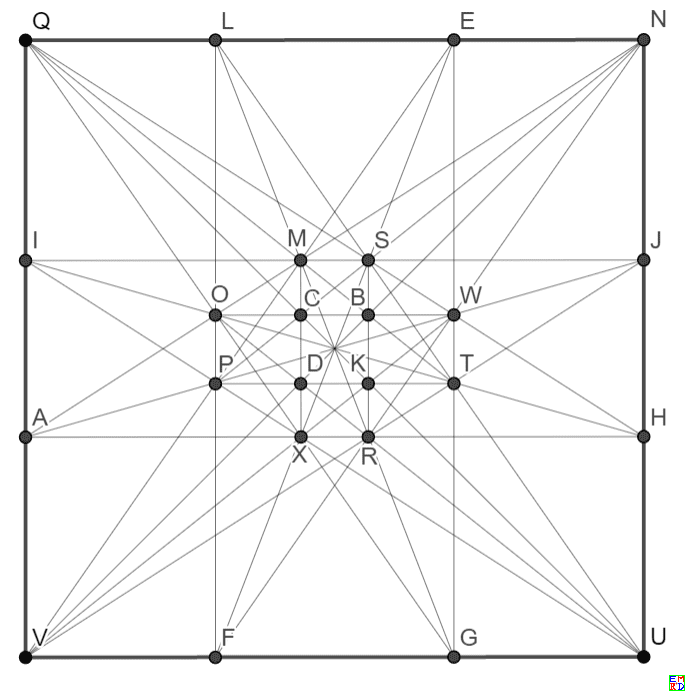
21棵24行对称解

21棵24行一个整数解竟然可以转化为3阶旋转对称的图 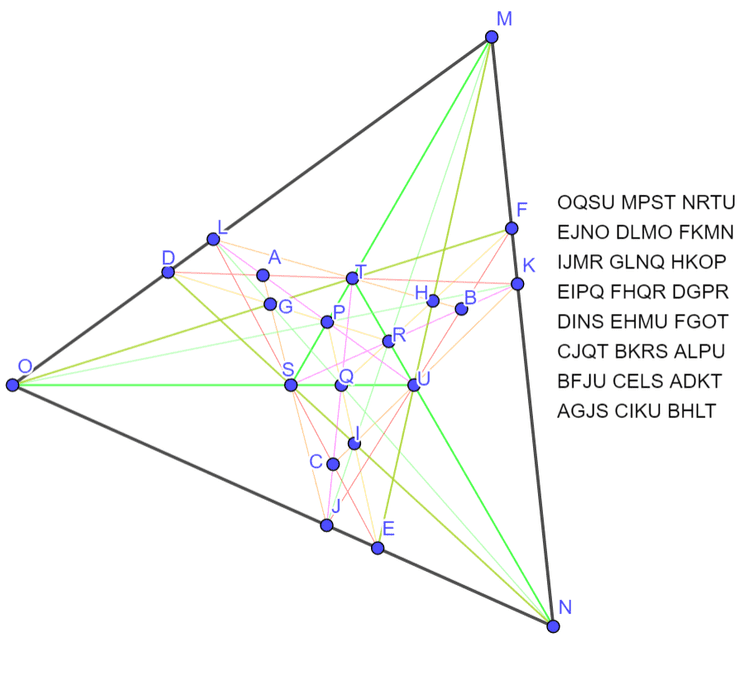t21.7 以及另外一组实数解也挺漂亮 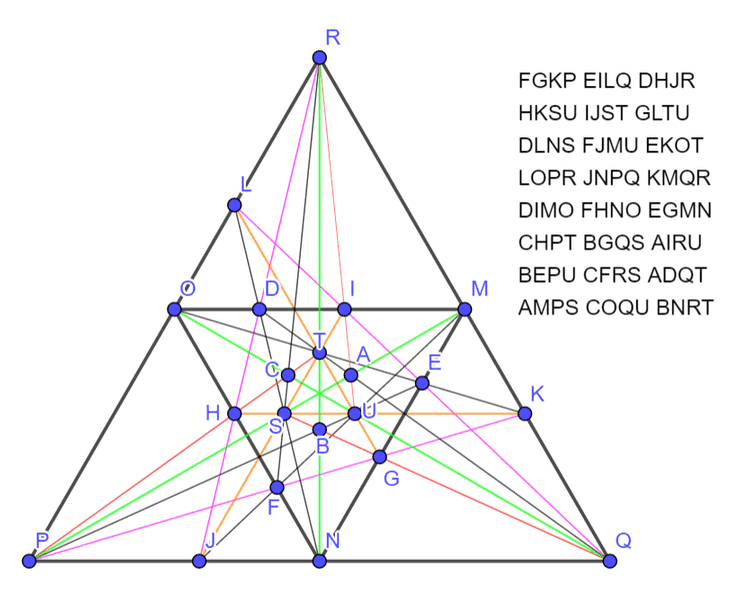t21.9 还有旋转飞镖形状的图形:
t21.10

使用nauty库计算自同构群的代码