完美相邻和之手串

Sun, 22nd December 2019Edit on Github手串数学算法

摘要

TSC999在2019年2月提问 :

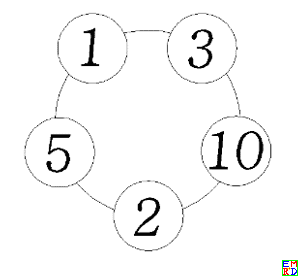
上图表示一个穿有五颗珠子的手串。每颗珠子上刻着一个数字，它们从小到大依次是 1、2、3、5、10。两颗相邻珠子上的数字之和是 4、6、7、12、13。三颗相邻珠子上的数字之和是 8、9、14、15、17。四颗相邻珠子上的数字之和是 11、16、18、19、20。五颗珠子上的数字之和是 21。

以上五组数字从小到大排列起来，是：1、2、3、4、5、6、7、8、9、10、11、12、13、14、15、16、17、18、19、20、21。从 1 到 21，不重复也不遗漏！

问题来了：如果手串是由六颗珠子穿成的，每颗珠子上也都刻有数字（其中一颗上刻的是 1），并且满足上述特性，那么这些数字是什么？它们在手串上是如何排列的？

对于六颗珠子的手串，本问题有解吗？

大家踊跃参与，最好搜索到了17棵珠子的结果并且定位到了OEIS中perfect different set ,并且和有限射影平面关联起来，得到不错的结果。

开始搜索

在问题提出的次日，TSC999用VB搜索出了所有的六颗珠子手串，其结果如果考虑其中一颗珠子上是数字 1，其余珠子上的数字假定是 x，y，z，u，v。
程序运行结果是：
k=1,x=2,y=5,z=4,u=6,v=13
k=1,x=2,y=7,z=4,u=12,v=5
k=1,x=3,y=2,z=7,u=8,v=10
k=1,x=3,y=6,z=2,u=5,v=14
k=1,x=5,y=12,z=4,u=7,v=2
k=1,x=7,y=3,z=2,u=4,v=14
k=1,x=10,y=8,z=7,u=2,v=3
k=1,x=13,y=6,z=4,u=5,v=2
k=1,x=14,y=4,z=2,u=3,v=7
k=1,x=14,y=5,z=2,u=6,v=3

【说明】程序给出了 10 个解答，但是其中 5 个是从手串背面观察的，手串翻转过来将与另 5 个解答相同。
因此真正的解答只有 5 组，见下图：

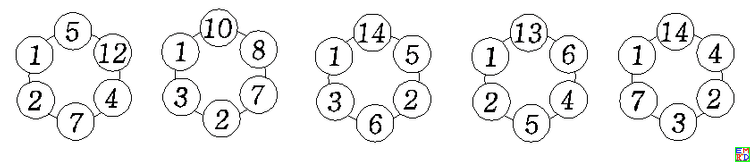
并且他提供了对应的VB代码。

wayne很快予以确认的确只有五组解，并且提供了TSC999需要的效率更高的Mathematica代码

n=6;
arr=a/@Range[n];
target=Flatten[{Total[arr],Table[Total[RotateLeft[arr,i][[1;;k]]],{i,0,n-1},{k,1,n-1}]}];
data=Subsets[Range[n (n-1)]+2,{n-2}];
Monitor[Reap[Timing[Do[tmp=Select[Permutations[Join[{2},data[[i]]]],Length[Tally[Differences[Sort[target/.Thread[arr->Join[{1},#]]]]]]==1&];If[Length[tmp]>0,Sow[tmp]],{i,Length[data]}]]],{i,Length[data]}]

其后TSC999得出不存在七颗珠子的手串。
wayne进一步改进其代码并且使用多核得出所有的八颗珠子的手串：

{{3,4,6,7,12,22},{{4,22,7,3,6,2,12},{12,2,6,3,7,22,4}}},
{{3,4,6,8,12,21},{{6,12,4,21,3,2,8},{8,2,3,21,4,12,6}}},
{{3,4,8,10,11,18},{{4,2,10,18,3,11,8},{8,11,3,18,10,2,4}}},
{{3,5,6,11,12,17},{{3,5,11,2,12,17,6},{6,17,12,2,11,5,3}}},
{{3,5,7,8,15,16},{{3,8,2,16,7,15,5},{5,15,7,16,2,8,3}}},
{{4,5,7,9,10,19},{{2,10,19,4,7,9,5},{5,9,7,4,19,10,2}}}

对应的Mathematica代码如下

n=8;
arr=a/@Range[n];
target=Flatten[{Total[arr],Table[Total[RotateLeft[arr,i][[1;;k]]],{i,0,n-1},{k,1,n-1}]}];
data=Select[IntegerPartitions[(-1+n) n-2,{n-2}],Length[Union[#]]==n-2&&Min[#]>2&];
Timing[ParallelTable[{d,Select[Permutations[Join[{2},d]],Length[Tally[Differences[Sort[target/.Thread[arr->Join[{1},#]]]]]]==1&]},{d,data}]]

并且穷举了九颗珠子的手串:

{{1, 14, 8, 2, 28, 3, 6, 7, 4}, {1, 4, 7, 6, 3, 28, 2, 8, 14}},
{{1, 8, 12, 2, 3, 13, 24, 4, 6}, {1, 6, 4, 24, 13, 3, 2, 12, 8}},
{{1, 16, 22, 2, 3, 4, 6, 8, 11}, {1, 11, 8, 6, 4, 3, 2, 22, 16}},
{{1, 2, 4, 8, 16, 5, 18, 9, 10}, {1, 10, 9, 18, 5, 16, 8, 4, 2}}

风云剑也提供了一段python代码。

此后mathe提供了一种手工穷举五颗珠子手串的方案 ,然后采用上面思路使用C代码编程计算到17颗珠子以内的结果:

N=1
1
N=2
1 2
N=3
1 2 4
N=4
1 3 2 7
4 1 2 6
N=5
3 1 5 2 10
N=6
1 3 6 2 5 14
1 7 3 2 4 14
1 3 2 7 8 10
5 1 2 7 4 12
1 2 5 4 6 13
N=7

N=8
4 1 12 2 6 3 7 22
10 2 4 1 8 11 3 18
6 1 3 5 11 2 12 17
2 8 3 1 5 15 7 16
3 2 8 1 6 12 4 21
10 2 1 5 9 7 4 19
N=9
3 6 7 4 1 14 8 2 28
4 6 1 8 12 2 3 13 24
16 1 11 8 6 4 3 2 22
9 10 1 2 4 8 16 5 18
N=10
1 5 4 13 3 8 7 12 2 36
10 3 11 1 4 2 20 8 9 23
1 4 3 10 2 9 14 16 6 26
18 1 3 9 11 6 8 2 5 28
11 9 6 1 18 3 2 8 4 29
18 6 2 1 10 4 16 5 7 22
N=11

N=12
21 12 5 1 7 2 22 4 16 3 11 29
1 15 5 3 25 2 7 4 6 12 14 39
10 9 2 15 16 6 7 1 4 20 3 40
1 4 7 3 16 2 6 17 20 9 13 35
20 19 4 1 11 2 8 7 25 6 3 27
2 6 1 4 16 3 15 10 12 14 17 33
9 1 7 13 12 3 11 5 18 4 2 48
1 8 10 5 7 21 4 2 11 3 26 35
1 22 14 20 5 13 8 3 4 2 10 31
12 3 1 25 7 6 5 9 8 2 21 34
6 1 3 8 9 5 19 23 16 13 2 28
23 3 1 8 5 2 18 11 10 22 6 24
1 14 10 20 7 6 3 2 17 4 8 41
1 14 3 2 4 7 21 8 25 10 12 26
4 14 8 9 2 1 24 5 10 6 7 43
4 14 2 1 9 13 6 5 27 8 7 37
12 14 2 1 7 13 18 4 5 6 19 32
12 2 1 5 16 11 7 10 9 4 25 31
N=13

N=14
5 4 22 8 6 1 10 2 16 32 20 3 21 33
12 1 14 4 5 11 10 7 22 3 38 2 6 48
3 9 10 1 5 2 24 15 29 14 21 13 4 33
8 4 1 14 7 10 6 24 9 2 18 25 3 52
8 19 1 4 6 31 3 13 2 7 14 12 17 46
31 1 4 20 2 12 3 6 7 33 11 8 10 35
4 2 14 15 17 7 18 1 8 3 10 23 5 56
27 12 3 5 11 2 4 26 14 9 1 28 7 34
5 9 1 12 11 6 2 18 16 35 21 4 3 40
2 16 6 5 8 4 3 25 21 9 1 33 14 36
27 23 5 1 8 16 10 12 19 2 11 4 3 42
22 10 1 17 8 5 24 14 2 4 3 12 27 34
7 2 8 5 16 19 1 3 24 6 12 14 11 55
14 20 7 12 3 1 9 8 28 2 24 5 6 44
25 6 5 3 1 12 22 7 17 2 18 10 23 32
21 8 1 25 23 4 10 2 3 17 11 7 6 45
10 1 15 34 2 3 17 7 6 8 4 19 9 48
15 12 7 1 2 21 17 11 5 9 4 26 6 47
14 5 7 13 2 1 8 21 17 18 33 4 6 34
18 4 13 16 7 1 2 28 14 5 6 9 12 48
N=15

N=16

N=17
5 10 19 1 7 31 2 11 3 9 36 17 4 22 6 18 72
24 5 33 15 3 7 1 34 12 19 9 4 17 6 14 2 68
14 9 28 17 1 3 12 10 31 7 27 2 6 5 19 20 62
12 7 1 23 11 3 2 13 33 22 6 4 17 9 41 25 44
11 21 1 27 8 7 2 3 26 25 16 14 4 6 13 39 50
13 10 29 5 17 18 1 2 4 8 16 32 27 26 11 9 45

wayne根据上面的搜索结果从OEIS网站找到了A058241 ，并发现问题等价于Perfect Difference Set

mathe的代码紧接着又找出了所有N=18的解:

N=18
9 26 1 17 2 10 4 7 38 5 8 24 15 42 6 22 3 68
17 14 1 7 3 27 6 12 23 5 19 2 51 9 4 16 34 57
2 8 12 31 3 26 1 6 9 32 18 5 14 21 4 13 11 91
6 1 11 26 35 20 2 8 13 4 15 9 5 31 3 50 16 52
4 34 1 27 3 13 2 6 50 5 9 11 12 10 7 19 41 53
4 12 17 5 23 2 24 15 31 6 3 10 1 7 35 32 36 44
1 14 39 19 2 10 28 8 35 6 3 13 4 7 18 5 32 63
16 5 34 12 1 30 2 8 17 37 7 4 15 3 6 14 36 60
6 4 18 39 1 41 7 17 8 5 14 2 31 3 9 11 15 76
8 7 4 6 23 1 12 9 5 38 16 28 3 32 37 2 18 58
17 32 4 24 5 1 13 25 2 10 8 3 52 26 9 7 15 54
3 8 2 15 16 32 7 29 1 5 14 4 22 12 9 50 27 51
29 25 16 30 1 5 9 8 4 7 32 24 18 2 35 3 10 49
17 28 1 12 36 19 25 7 11 4 5 30 3 21 2 8 6 72
14 1 12 23 3 7 21 16 18 22 2 6 11 32 20 5 4 90
12 4 25 2 5 1 9 13 40 11 3 21 26 19 20 18 34 44
4 5 1 19 3 12 2 16 43 8 13 26 24 7 41 27 11 45
24 1 15 28 6 12 11 3 5 2 20 36 35 13 4 38 9 45
13 27 4 1 15 26 8 30 18 7 3 9 2 22 29 6 17 70
27 4 1 35 15 33 25 39 14 8 16 18 3 7 2 11 6 43
12 2 20 9 16 8 13 17 6 4 1 51 19 7 32 3 15 72
36 10 1 4 16 7 17 25 8 26 3 6 13 39 2 12 18 64
7 6 3 14 8 12 27 19 2 24 18 10 1 4 36 35 32 49
28 7 17 3 18 19 13 1 9 2 4 43 36 5 26 8 22 46
1 22 20 7 9 10 5 29 3 8 17 13 48 4 2 12 21 76
31 27 8 15 3 14 16 12 9 1 19 5 39 36 7 4 2 59
2 4 27 9 5 3 12 1 22 32 19 7 11 28 25 24 10 66
14 20 1 30 37 23 15 10 16 2 4 7 33 9 3 5 19 59
35 22 6 13 21 18 9 11 5 26 23 1 29 3 4 8 2 71
43 1 17 9 31 6 2 12 16 5 47 3 4 15 10 13 11 62
37 3 4 10 1 5 22 24 12 13 8 26 9 30 2 29 19 53
1 4 2 16 12 13 8 24 38 44 15 27 10 9 17 3 11 53
14 34 16 10 15 12 1 4 3 36 23 6 18 22 9 2 19 63
6 13 14 8 9 11 1 3 34 2 45 7 18 5 48 16 10 57
7 10 20 5 13 11 3 1 8 31 44 2 19 26 34 16 6 51
38 14 21 1 3 8 45 9 18 10 6 7 17 2 29 15 5 59
1 3 11 20 7 33 10 9 17 22 6 2 16 5 32 12 13 88
2 17 14 8 1 3 25 7 20 30 46 15 38 10 6 5 13 47
9 20 3 1 6 8 26 11 5 12 31 22 13 36 25 2 19 58
13 8 31 17 1 9 2 3 23 7 43 4 20 16 6 19 34 51
10 17 1 7 15 24 20 9 2 3 38 13 6 26 4 12 21 79
2 3 12 6 7 19 8 14 36 1 9 29 4 20 11 45 16 65
21 35 14 23 10 1 6 36 9 16 13 26 2 3 15 4 8 65
10 27 19 24 12 13 32 8 1 6 11 3 2 28 34 35 4 38
1 37 11 24 26 16 29 23 18 33 6 8 13 4 3 2 10 43
12 6 20 2 1 8 5 19 34 10 7 39 4 21 27 30 15 47
6 8 1 2 27 7 13 5 21 22 19 12 4 24 32 10 23 71
7 8 11 16 13 32 12 5 33 1 2 18 4 6 37 9 14 79
1 2 41 12 5 6 8 7 9 4 29 36 18 22 10 27 25 45
38 25 12 16 4 15 24 2 1 6 49 11 10 8 5 17 14 50
10 9 16 5 1 2 42 13 4 11 23 14 12 20 7 29 18 71

有限射影平面

此后mathe找到了一篇关于Perfect Difference Set的文章 ,里面给出一种使用有限射影平面构造特殊解的方案:
文章主要思路如下：
如果我们要找 $K$ 棵珠子的手串，其中 $K=p^e+1$ ,其中 $p$ 是素数，记 $r=p^e,q=r^2+r+1$ , 我们计算的和将要覆盖1,2,...,q。我们先选择r阶有限域 $F_r$ ,比如取r=3,那么就是模3运算。另外我们需要选择 $F_{r^3}$ 中一个生成元g, 比如说我们选择 $g$ 使得 $g^3=g-1$ ,于是 $F_{3r}$ 中任意一个元素可以写成 $a+bg+cg^2$ 形式，其中a,b,c都是 $F_r$ 中元素（也就是0,1,2)。
经计算可以得知这样选择的g的阶是 $3^3-1=26$ ,所以验证了g是生成元，也就是 $F_{r^3}$ 中任意一个非零元还可以写成 $g^h$ 的形式，其中 $0\le h\le r^3-2=25$ 。由于，对于任意h满足 $0\le h\le r^3-2$ ,存在唯一的 $a_h,b_h,c_h$ 使得 $g^h=a_h+b_hg+c_hg^2$ ，我们记 $h=H(a_h,b_h,c_h)$ 或 $h=H(a_h+b_hg+c_hg^2)$
现在我们把 $F_{r^3}$ 中任意一个非零元素 $a+bg+cg^2$ 看成 $F_r$ 中射影平面上一个点 $(a,b,c)$ ,那么需要注意如果有两个点u,v使得 $H(u)-H(v)$ 是q的倍数，那么它们表示的是射影平面上的同一个点，或者说存在 $k\in F_r^{\times }$ 使得u的每个分量都是v对应分量的k倍。文章证明对于此射影平面任意直线上的点列 $P_0,P_1,...,P_r$ (每条直线上正好r+1个点), 那么 $H(P_0),H(P_1),...,H(P_r)$ 两两差关于q的余数各不相同。
比如我们选择直线 $z=0$ ,所以上面的点分别为 $(1,0,0), (0,1,0), (1,1,0),(1,2,0)$
对应 $F_{r^3}$ 中的数 $1,g,1+g,1+2g$ ,对应 $g^0,g^1,g^9,g^3$ ,所以我们选中了数 $0,1,3,9$ ，选中的数中必然有两个数相差1，通过平移将它们变为0和1，这里这一步可以省略
所以两两差模 $q=13$ 分别为 $1,3,9, 12, 2, 8, 10, 11, 6, 4, 5, 7$ 互不相同，验证了我们的结论。对应4棵珠子为 $1-0=1,3-1=2,9-3=6,13-9=4$
选择不同的直线结果会相同。为了获取不同的结果，我们需要选择不同的生成元g，对应的，相当于找到 $H(P_0),H(P_1),...,H(P_r)$ ，我们将每个 $H(.)$ 在乘上一个和q互素的数字在模q就可以得到在不同坐标系下的 $H(.)$
比如，我们可以将 $g^0,g^1,g^9,g^3$ 全部指数乘以2得到 $g^0,g^2,g^5,g^6$ ,然后平移为 $g^8, g^10, g^0,g^1$ ,对应四颗珠子为 $1-0=1,8-1=7,10-1=2,13-10=3$ . 通过这种方法，我们可以在 $O(r^6)$ 的时间内构造出所有的解，但是这种方法不能证明不存在其它解.

其中，含 $k+1$ 颗珠子的手串的构造的解的数目满足下面表格的最后一列的数目

$k=p^n$	p	n	$q=k^2+k+1$	$\frac{\varphi(q)}{6n}$
3	3	1	13	2
4	2	2	21	1
5	5	1	31	5
7	7	1	57	6
8	2	3	73	4
9	3	2	91	6
11	11	1	133	18
13	13	1	183	20
16	2	4	273	6
17	17	1	307	51
19	19	1	831	42
23	23	1	553	78
25	5	2	651	30
27	3	3	757	42
29	29	1	871	132
31	31	1	993	110
32	2	5	1057	30

可以看出到现在为止找到的解都是符合文章模式的解。
另外mathe找到了另外一篇关于有限射影平面的文章 , 里面说如果 $n\equiv 1 (\mod 4)$ 或者 $n \equiv 2(\mod 4)$ 而且n包含4k+3形式的素因子的奇数次方，那么不存在长度为n+1的手串.
由此我们可以在A058241 后面添加三个零。
mathe还给出了一段Pari/gp代码实现上面的构造方法, 使用方法如下：

(11:34) gp > normresult(8)
%216 =
[1 2 10 19  4  7  9  5]

[1 8 11  3 18 10  2  4]

[1 3  8  2 16  7 15  5]

[1 6 17 12  2 11  5  3]

[1 4 22  7  3  6  2 12]

[1 6 12  4 21  3  2  8]