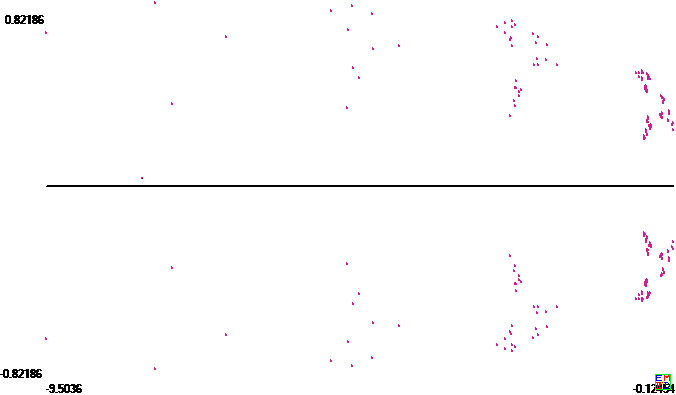数学星空于2015年底提问 :
对于a(n+1)=a(n)+a(n)21,a(1)=1,
我们可以利用微分方程求解a(n)的第一阶项.
设a(n)=y
又a(n+1)−a(n)=a′(n)
则有y′y2=1
求解得到:a(n)=y≈(3n)31
接下来,我们可设
(a(n))3=3n+a+bln(n)+nc+n2d+n3e+n4f+…
本主题的任务是如何求解a,b,c,d,e?
或者利用数学计算软件或者数学理论给出更精确的表达式?
注:Kuing(郭子伟)已证明(P111,kuingluing20151222)
(3n)31<a(n)<(3n)31+(3n)−31
并指出(彩色の夢∩o∩)给出下面结果,但并未给出证明过程:
(a(n))3=3n+2+ln(n+2)−9n+61−ln(5)+151
最终我们通过努力,得出这个数列的无穷项展开形式。而且这种方法可以使用在很多类似的数列上,比如:
2010年初数学星空提问的一个数列不等式 也可以用类似方法分析:
若数列an满足 :
a1=21,an+1=21(an2+1)
则: 1−n2+n22ln(3n)+128n2417≤an≤1−n2+2n25lnn+3
初步逼近
mathe很快给出如下分析方案 :
a(n+1)=a(n)+a(n)21
得出
a(n+1)3=a(n)3+3+a(n)33+a(n)61
归纳容易得出对于n≥2有a(n)3≥3n+2于是重新代入上面得出
a(n)3≤8+3(n−2)+3∑k=2n−13k+21+∑k=2n−1(3k+2)21
然后我们可以利用积分估算得出
a(n)3≤8+3(n−2)+ln(3(n−1)+2)−ln(8)+81−3(n−1)+21=3n+ln(3n−1)−3n−11+81+2−ln(8)<3n+2+ln(n)
而在得到这个上界后,我们有可以利用它来估计下界得出
a(n)3≥8+3(n−2)+3∑k=2n−13n+2+ln(n)1
而且容易看出后面求和式3∑k=2n−13n+21的差在n趋向无穷收敛到一个常数
所以可以知道存在常数C是的a(n)3≥3n+ln(n)+C
也就是我们可以非常轻松证明a(n)3−3n−ln(n)有界,进一步分析还可以得出其极限存在,但是求这个极限比较有难度
而数值计算Δ(n)=a(n)3−3n−ln(n),有
Δ(10)=1.220832
Δ(100)=1.151530
Δ(1000)=1.137657
Δ(10000)=1.135573
Δ(100000)=1.135295
Δ(1000000)=1.135261
Δ(10000000)=1.135256
所以可以看出1#彩色の夢∩o∩)估计公式中常数项偏离比较大,倒是本楼开头估计是中对应常数项ln(3)+81+2−ln(8)只略微大了一些
同样要数值计算这个极限值,也可以先计算前面若干项,然后对于余下部分求和式和近似公式求差值,而差值部分误差可以非常容易估计,这样就可以得出极限值一个较好的估计范围了。
无穷展开
次日Buffalo给出了一个神奇的含ln(n)的无穷展开式形式 :
首先令bn=an3,得到bn+1=bn+3+bn3+bn21。渐近式前三项当然是3n+lnn+a,但是后面的项可不是n1的简单级数,而应该是∑i=1∞niPi(lnn,a),这里的Pi(lnn,a)是lnn的i次多项式(事实上同时也是a的i次多项式)。用待定系数法,令fm(n)=3n+lnn+a+∑i=1mniPi(lnn,a)让mathematica在n=∞处展开fm(n+1)−fm(n)−3−fm(n)3−fm(n)21到O(nm+11)逐次得到Pi(lnn,a)。计算发现Pi(lnn,a)实际上很神奇地仅仅是是lnn+a的i次多项式,而且系数有很明显的规律,可以把一部分项合并降低次数,目前做到bn≈3n+lnn+a+ln(1+3nlnn+a)−6(3n+lnn+a)5+3n+lnn+aln(1+3nlnn+a)+∑i=2∞ni+2Qi(lnn+a),想进一步降低多项式次数遇到数列{270, 870, 1725, 2780, 4000, 5361},找不到规律。
前的结果用于快速计算任意初值的数列极限值已经足够了:已经知道bn≈3n+lnn+a+ln(1+3nlnn+a)−6(3n+lnn+a)5+3n+lnn+aln(1+3nlnn+a)−6n21+∑i=1∞ni+2Qi(lnn+a),从初值出发计算N项,定义Δ(n)=bn−3n−lnn,Δ(N)就是极限a的粗略值d0,然后令di+1=Δ(N)−ln(1+3NlnN+di)+6(3N+lnN+di)5−3N+lnN+diln(1+3NlnN+di)+6N21,这样迭代数次直至结果不变,这个值和真实极限值的误差是O(N3lnN)。
费点功夫把展开式多计算几项就可以得到更好的逼近效果O(Ni+2(lnN)i)。
作为例子,选初值为1,计算100项,迭代几次后得到极限值为1.1352567349497837,计算10000项,迭代几次后得到极限值为1.1352558474127066,两者相差8.9×10−7,小于估计的O(N3lnN)≈5×10−6
假设已经求得初值为b1的数列的通式bn=f(n,b1)≈3n+lnn+hb1+R(n,a(b1)),现在来看对极限值hb1我们能了解到什么程度。
递推方程是平移不变的,因此f(n,bi)=f(n,f(i,b1))=f(n+i−1,b1),所以有hbi=limn→∞(f(n,bi)−3n−lnn)=limn→∞f(n+i−1,b1)−3n−lnn=hb1+3i−3,这是个严格的等式。由bi=f(i,b1)≈3i+lni+hb1+R(i,hb1)可以迭代求得3i≈bi−ln3bi−hb1+...,最后得到hx≈x−ln3x−3+6x5+3x22+108x377+240x4133−5400x52669−567x61676+O(x71)。非常神奇的是尽管f(n,a)里含有巨量的lnn+a,可是后面的项里面不仅hb1合情合理地消失了,连lnx也无影无踪。
对于很大的初值b1,可以直接用这个表达式作为近似值。如果b1不太大,可以先迭代i−1次得到较大的bi,算出hbi,然后用等式hb1=hbi−3i+3计算。
mathe对Buffalo的结果做进一步推导 :
对于bn+1=bn+3+bn3+bn21,假设
bn=3n+ln(n)+a+∑k=1+∞nkPk(ln(n)+a)
我们先查看(n+1)kPk(ln(n+1)+a)=nk×(1+n1)kPk(ln(n)+a+ln(1+n1)),
这个式子展开后是一个无穷级数,可以写成形如∑h=k+∞nhQk,h(ln(n)+a)的级数,其中
每个Qk,h(.)都是次数不超过k的多项式,而且同a无关。
所以从形式上,这种形式的级数应该是可以用于这种递推式的,但是得出的结果不一定是收敛的,如同Γ函数的Stirling级数就是不收敛的,而只是一种渐近式。
为了计算方便,我们可以将bn=3n+ln(n)+a+∑k=1+∞nkPk(ln(n)+a)中n用y1代替,而ln(n)+a用X代替,写成形式级数
bn=y3+X+∑k=1+∞Pk(X)yk
而其中如果我们将y替换为1+yy,然后再将X替换为X+ln(1+y),就可以得出bn+1=y3(1+y)+X+ln(1+y)+∑k=1+∞(1+y)kPk(X+ln(1+y))yk
然后代入原始递推式即可。
比如在Pari/Gp,我们可以输入
(16:47) gp > 3/y+X+(b00+b01\times X)\times y+(b10+b11\times X+b12\times X^2)\times y^2+O(y^3)
%1 = 3\times y^-1 + X + (b01\times X + b00)\times y + (b12\times X^2 + b11\times X + b10)\times y^2 + O(y^3) //这个即$b_n$二阶近似
(16:49) gp > subst(%1,y, y/(1+y))
%3 = 3\times y^-1 + (X + 3) + (b01\times X + b00)\times y + (b12\times X^2 + (-b01 + b11)\times X + (-b00 + b10))\times y^2 + O(y^3)
(16:51) gp > subst(%3,X,X+log(1+y))
%4 = 3\times y^-1 + (X + 3) + (b01\times X + (b00 + 1))\times y + (b12\times X^2 + (-b01 + b11)\times X + (-b00 + (b01 + (b10 - 1/2))))\times y^2 + O(y^3)//这个为$b_{n+1}$的二阶近似
(16:52) gp > %4-%1-3-3/%1-1/%1^2
%6 = ((-b01 + 1/3)\times X + (-b00 + (b01 - 11/18)))\times y^2 + O(y^3)
由此得出b01=1/3,b00=-5/18.
类似可以得出
bn=3n+ln(n)+a+n31(ln(n)+a)−185+n2−181(ln(n)+a)2+5411(ln(n)+a)−61+n3811(ln(n)+a)3−817(ln(n)+a)2+16229(ln(n)+a)−1458157+n4−3241(ln(n)+a)4+2438(ln(n)+a)3−972115(ln(n)+a)2+729122(ln(n)+a)−17496013327+...
公式:
∑k=1+∞(1+y)kPk(X+ln(1+y))yk−∑k=1+∞Pk(X)yk=bn3+bn21
(y3+X+∑k=1+∞Pk(X)yk)2(∑k=1+∞(1+y)kPk(X+∑h=1∞h(−1)h−1yh)yk−∑k=1+∞Pk(X)yk)=3(y3+X+∑k=1+∞Pk(X)yk)+1
上面表达式中常数a的值的计算是一个大问题,Buffalo最早给出了7位左右的精度,后来wayne 和mathe都尝试予以改进, Buffalo 随后给出了
30位精度的值1.135255847315503714195394347748。
快速计算方案
Buffalo随后表示:
绕开数列通式的渐近式直接快速求极限值的渐近展开式方法。
根据前面的分析,我们知道h(bi)=h(b1)+3i−3,因为b2=b1+3+b13+b121,所以h(x)应该满足函数方程h(x+3+x3+x21)=h(x)+3,从这个函数方程即可快速求得极限值a(x)的渐近式:前面的几项为
h(x)≈x−ln3x−3+6x5+3x22+108x377+240x4133−5400x52669−567x61676−317520x7788279+362880x87762807+12247200x9886072583−111375x1021193112−28226880x1151269552749+14010796800x1213179813953723+127498250880x137041436522468181+1218979125x1497349629390438+⋯
除了系数可以乘以n(n+1)!3n化为整数实在是看不出规律,连符号都无法预测。
公式证明
mathe尝试对上面的计算过程给出比较严格的证明过程 :
记f(x)=x+3+x3+x21,f1(x)=f(x),fk+1(x)=f(fk(x))。那么fk(x)相当于保持数列b(n)递推关系不变,但是第零项b(0)改变成x,那么第k项就变为fk(x)了。
设y=g(a,m)为使得n→∞limfn(y)−3(n+m)−ln(n+m)=a的数而且y≥2 。
根据前面的分析过程,不管数列fn(y)中第零项y是多少,极限n→∞limfn(y)−3n−ln(n)都是存在的,
于是对于给定的m极限n→∞limfn(y)−3(n+m)−ln(n+m)也存在只是和前一个极限差了常数3m。
于是y=g(a,m)表示如果保持数列b(n)的递推关系,其中第m项b(m)为y,那么n→∞limb(n)−3n−ln(n)的极限正好为a。
而比较有意思的是这时候的m我们可以推广到任意一个实数而不仅仅是整数,从而将数列ba(m)推广为一个定义在正实数范围以m为自变量的函数
于是容易得出g(a,m)=g(a+3d,m−d),而且对于我们以前定义的ba(m)=g(a,m)
而根据前面分析应该有g(a,n)≈3n+ln(n)+a+∑k=1∞nkPk(ln(n)+a)
由于g(a,n)=g(a−3d,n+d),如果我们选择适当d使得ln(n+d)+a−3d=0,记其中m=n+d,得到
那么结果可以简化为g(a,n)=g(a−3d,m)≈3m+∑k=1∞mkPk(0).
由此,对于任意n,ba(n)=g(a,n), 如果我们可以先利用上面公式反解出对应的m,就可以求出对应的d=m−n,然后利用a=3d−log(m)得出a.
于是问题就变成求渐进式s(x)≈3x+∑k=1∞xkPk(0),以及其逆函数.
然后我们假设当将n替换成n+1时,对应的m变化为m′,于是根据m的定义必然有m′−3ln(m′)=m+1−3ln(m)
这里m′可以看成是m的隐函数,显然可以看出在m→∞时,m′=m+1+o(1),代入递推式m′=m+1+3ln(mm′),可以看出对于一般情况的f,这里m′,m之间关系式直同f中常数项相关
得出m′=m+1+3m1+o(m1),反复迭代可以得出m′=J(m)=m+1+3m1−18m21−54m31+324m47+…
系数依次为31,−181,−541,3247,−486031,−29160107,6123602833,−459270621,…
然后再次利用公式ba(n+1)=ba(n)+3+ba(n)3+ba(n)21,并且ba(n+1)=s(m′),ba(n)=s(m),将m′=J(m)代入,
也就是求s(J(m))=s(m)+3+s(m)3+s(m)21
比较系数,就可以得出Pk(0)的值,
分别为−185,−61,−1458157,−17496013327,−7873200444191,−33067440014533499,−20832487200776933609
从前面的结果来看都是负数而且绝对值小于1,也就是级数很可能是收敛的
于是H(x)=s(x1)1满足H(0)=0而且展开式非常容易算出,于是H的逆函数在0的展开式也可以计算出来,由此可以得出s的逆函数的展开式,也是罗兰级数形式.
可以用来计算更高精度结构,然后结果再倒数一下可以得到s的逆函数形式,也就是可以用ba(n)直接计算对应的m,最后可以推导出对应的a
最后m的公式应该是31x+18x5+2x21+324x3239+6480x45227+….
前面得出m(x)的形式是m(x)=3x+∑k=1∞xkuk。于是当x取bn得出结果为m,而当x取bn+1时得到结果为m′,那么m′和m恰好有关系m′=J(m).
也就是J(m(x))=m(x+3+x3+x21).
由此直接可以解出m(x)的系数.
在得到m(x)后可以求出对应的m再求出a.在得到a和给定项数n,那么可以先算m使得m−3ln(m)=n+3a,然后就可以用m→x的函数s求出这一项的值.
现在比如选择b30=94.577173180254437058800379657718614759
那么根据前4项可得m=31.5287182224435829596913315304969568,a=1.13525584723432304669623826092662724,精度在8位
如果b1000=3008.045412232225615137583957841337992049977740047149556926283
那么根据m(x)前4项可得m=1002.681896477635973673360401688986574721554051620745012411842,a=1.1352558473155037114596749643830028099868785719581459235494458精度在17位,基本接近x51左右的精度.
而如果我们计算m(x)更多项数,就可以有更好的收敛精度,甚至对于较小的x也可以计算出高精度的a.
推广
wayne随后提出对问题进行一般化推广
此题目抽象出来,本质上是一个非线性函数在无穷迭代后的函数性态分析。
设x1=1, xn=g(xn−1)=g(g(xn−2))=....g(n−1)(x1)
在本题里面,
对于a数列,x1=1,g(x)=x+x21
对于b数列,x1=1,g(x)=x(1+x1)3
我们可否站在这个层面,即通过分析g(x)的函数性态,来分析对于给定的点x0,g(n)(x0)的稳定性态。
比如,x1=1,n→+∞, g(n)(x1)≈f(n)+c,求f(n)和c。 更进一步,f(n)和c是否跟初始值x1无关?
比如,x1=x,h(x)=g(+∞)(x) ,求h(x)?
mathe认为:
一般情况是迭代x1=g(x0),..xn=g(xn−1)=..=gn(x0)有一个不动点x.,也就是x.=g(x.),而且迭代过程会收敛到x.,我们需要分析收敛情况.
我们可以先做分式线性变换h(x)=g(x1+x.)−x.1,将不动点变化到无穷远点。而对于本题中,是属于单侧接近x.,对应可以转化为迭代充分大次数后数值单调增到无穷大
设g(x)=x.+∑k=1∞ak(x−x.)k, 如果a1<1那么会收敛比较快,那么如果其中a1=1于是收敛会很慢,其中
h(x)=∑k=1∞xkak1=x+∑k=0∞xkbk
而对于特殊迭代h(x)=x+xhu,可以利用xn+1h+1=xnh+1+uh+…来替换成b0=0的模式.
当然如果只分析收敛速度,就不需要展开这么多项,基本只要分析常数项b0的值即可.
Buffalo给出了公式形式:
对于方程an+1=αan+anmPk(n),Pk(n)=∑i=0kβini(所有参数都大于零)有以下一般性结论
- 若α>1,则an≈cαn+...
- 若α=1,则an≈(k+1m+1βknk+1)m+11+...
- 若0<α<1,则an≈(1−αβknk)m+11+...
α≥1时上面的结论没问题。
0<α<1时用代换an=(1−αβknk)m+11bn重新定标得到方程bn+1=αbn+bnm1−α+o(n1)。
非线性极限普适方程Sn+1=αSn+Snm1−α有不动点,情况比较复杂。随着m的取值变化数列的“极限”会出现分岔、混沌现象。第一个分岔点在m=1−α1+α处。
记g(1)(x)=g(x)=x2(1+x)3,g(k+1)(x)=g(g(k)(x))我们知道h(g(x))=h(x)+3
那么我们知道对于所有n>0,方程g(n)(x)=x的解都必然是h(x)的非解析点.
试做了一下g(5)(x)=x的零点图如下
Buffalo做了总结:
做个小结:
考察满足递推关系an+1=αan+anmPk(n)的初值为x的数列的极限行为。这里的Pk(n)=∑i=0kαini,不妨设αk=1。所有的参数都是非负正实数,特别是m也不限于整数。现在根据α取值范围分情况讨论。
- α>1
此时an≈h(x)αn−1+h(x)mQk(n)α−mn+⋯。多项式Qk(n)满足Qk(n+1)−αm+1Qk(n)=α2mPk(n)。第二项已经很小了,后面的没必要计算下去。
若Pk(n)=1,则h(x)满足h(αx+xm1)=αh(x),由这个等式可以求得h(x)≈x(1+(αm+1−1)xm+1αm−∑i=2∞(i−1)!m∏j=1i(α(m+1)j−1)R(i,αm+1)(−xm+1αm)i)。R(i,t)是的t的2i(i−1)−1次多项式,系数除了1次、2i(i−1)−2次为零之外都是m的i−2次正整系数多项式,而且2i(i−1)−1次系数为m!(m+i−2)!,常数项为∏j=1i−2(im+j),二次项系数为(i−2)(m+1)∏j=2i−2(im+j)。
前几个R(i,t)是R(2,t)=1,R(3,t)=3m+1+(m+1)t2。
- 0<α<1
作代换an=(1−ααknk)m+11bn可以得到bn+1=αbn+bnm1−α+O(n1)。普适极限方程Sn+1=αSn+Snm1−α有不动点Sn=1,随着参数的变化数列的趋势会出现分岔、混沌现象。当0<m<1−α1+α时Sn→1,m>1−α1+α时不动点不稳定,开始变成两周期以至更长周期的循环,而且很快就变成混沌的。
- α=1
作代换bn=anm+1可以得到bn+1=bn+m+1+∑i=2∞Cm+1i(bnPk(n))i−1,所以bn≈Qk+1(n)+2mlnn+h(Pk,x)+O(nlnn),多项式Qk+1(n)满足Qk+1(n+1)−Qk+1(n)=Pk(n)。
如果Pk(n)=1可以进一步得到bn≈(m+1)n+2mln(n+m+12mlnn+h(x))+h(x)−12((m+1)n+2mlnn+h(x))m(2m+1)+(m+1)x+2mlnn+h(x)4m2ln(1+2(m+1)n2mlnn+h(x))−48(m+1)2n27m3+4m2+∑i=3∞niRi−2(2mlnn+h(x))
这时候h(x)满足h(xm(1+x)m+1)=h(x)+m+1,h(x)≈x−2mlnm+1x−(m+1)+12xm(2m+1)+48x2m2(3m+2)+⋯。后面的−k次项系数含m((k+1)m+k)因子,如果k是偶数还有一个额外的m因子。
更多计算结果
数学星空试着对更多递推数列进行类似计算 ,得出
对于an+1=an+an21
1.令bn=an3,得到
bn+1=bn+3+bn3+bn21
2.由m′−3ln(m′)=m+1−3ln(m)渐近展开:
m′=J(m)=m+1+3m1−18m21−54m31+324m47−4860m531−29160m6107+612360m72833−459270m8641−2755620m93001+66134880m1087961−2182451040m11817951−65473531200m1224880117+2553467716800m131118093573−612832252032m1467495517−4178401718400m15603350659+965210796950400m16150300871447+⋯
3.由m(x+3+x3+x21)=J(m(x)),设m(x)=3x+∑k=1∞xkuk,渐近展开:
m(x)=3x+18x5+2x21+324x3239+6480x45227+32400x57297−226800x6382271−3175200x712524549+342921600x8709670963+1028764800x928761656717−226328256000x106137702104697−829870272000x11516199738730261−4369266982080000x121429968790523743403+113600941534080000x132050189135375425012401+795206590738560000x1435895037045177279350019−9542479088862720000x156198573918031962345943781−16031364869289369600x1653515807461516509490031169+⋯
4.极限值a0由下式求出:
m(an)−3ln(m(an))=n+3a0
5.关于bn渐近展开式计算:y=n1,X=ln(n)+a0
F1=f(y,X)=y3+X+(b00+b01X)y+(b10+b11X+b12X2)y2+(b20+b21X+b22X2+b23X3)y3+(b30+b31X+b32X2+b33X3+b34X4)y4+(b40+b41X+b42X2+b43X3+b44X4+b45X5)y5+(b50+b51X+b52X2+b53X3+b54X4+b55X5+b56X6)y6+(b60+b61X+b62X2+b63X3+b64X4+b65X5+b66X6+b67X7)y7+(b70+b71X+b72X2+b73X3+b74X4+b75X5+b76X6+b77X7+b78X8)y8+⋯
F2=f(1+yy,X+ln(1+y))
由F2=F1+3+F13+F121求解得到:
b00=18−5,b01=31,b10=6−1,b11=5411,b12=18−1,b20=1458−157,b21=16229,b22=81−7,b23=811,b30=174960−13327,b31=729122,b32=972−115,b33=2438,b34=324−1,b40=7873200−444191,b41=13122020647
b42=8748−1321,b43=2187139,b44=2916−35,b45=12151,b50=330674400−14533499,b51=944784138391,b52=157464−28573,b53=787328273,b54=6561−200,b55=43740187,b56=4374−1,b60=20832487200−777322409,b61=24800580033909461
b62=314928−65179,b63=131222047,b64=17496−1097,b65=1312201787,b66=131220−197,b67=153091
类似于mathe提供的求解思路,我们来讨论稍一般的情形
对于an+1=an+ank−11
1.令ank=bn,得到
bn+1=bn+k+2bnk(k−1)+6bn2k(k−1)(k−2)+24bn3k(k−1)(k−2)(k−3)+120bn4k(k−1)(k−2)(k−3)(k−4)+720bn5k(k−1)(k−2)(k−3)(k−4)(k−5)+⋯
2.由m′−kln(m′)=m+1−kln(m)渐近展开:
m′=J(m)=m+1+km1−2k2m2k−2+6(k3m3)−9k+6+2k2−12k4m43k3−22k2+36k−12+60k5m512k4−125k3+350k2−300k+60−120k6m6−120+900k−1700k2+1125k3−274k4+20k5+840k7m7−8820k+24500k2−25725k3+11368k4+840−2058k5+120k6−2520k8m8−2520+35280k+315k7−6534k6−135240k2+205800k3−142149k4+45962k5+2520k9m9−45360k+229320k2−476280k3+471429k4+2520−235494k5+59062k6−6849k7+280k8−10080k10m10−1461600k2+3969000k3−5314932k4+3770550k5+226800k−1447360k6+293175k7−28516k8+1008k9−10080+⋯
3.由m(x+k+2xk(k−1)+6x2k(k−1)(k−2)+24x3k(k−1)(k−2)(k−3)+120x4k(k−1)(k−2)(k−3)(k−4)+720x5k(k−1)(k−2)(k−3)(k−4)(k−5)+⋯)=J(m(x))
设m(x)=kx+∑k=1∞xkuk,渐近展开:
注:上面m(x)形式解不正确,需要重新研究其形式才能求解渐近展开式
4.极限值a0由下式求出:
m(an)−kln(m(an))=n+ka0
5.关于bn渐近展开式计算:y=n1,X=ln(n)+a0
$F_1=f(y,X)=\frac{k}{y}+X+(b_{00}+b_{01}X)y+(b_{10}+b_{11}X+b_{12}X^2)y^2+(b_{20}+b_{21}X+b_{22}X^2+b_{23}X^3)y^3+(b_{30}+b_{31}X+b_{32}X^2+b_{33}X^3+b_{34}X^4)y^4+(b_{40}+b_{41}X+b_{42}X^2+b_{43}X^3+b_{44}X^4+b_{45}X^5)y^5+(b_{50}+b_{51}X+b_{52}X^2+b_{53}X^3+b_{54}X^4+b_{55}X^5+b_{56}X^6)y^6+(b_{60}+b_{61}X+b_{62}X^2+b_{63}X^3+b_{64}X^4+b_{65}X^5+b_{66}X^6+b_{67}X^7)y^7+(b_{70}+b_{71}X+b_{72}X^2+b_{73}X^3+b_{74}X^4+b_{75}X^5+b_{76}X^6+b_{77}X^7+b_{78}X^8)y^8+\cdots$
F2=f(1+yy,X+ln(1+y))
由F2=x+k+2F1k(k−1)+6F12k(k−1)(k−2)+24F13k(k−1)(k−2)(k−3)+120F14k(k−1)(k−2)(k−3)(k−4)+720F15k(k−1)(k−2)(k−3)(k−4)(k−5)+⋯求解得到:
注:上面F1形式解不正确,需要重新研究其形式才能求解渐近展开式
对于k=4,我们可以得到:
对于an+1=an+an31
1.令an4=bn,得到
bn+1=bn+4+bn6+bn24+bn31
2.由m′−83ln(m′)=m+1−83ln(m)渐近展开:
m′=J(m)=m+1+8m3−64m23−512m317+4096m4105−163840m5297−1310720m611111+14680064m776737+587202560m8492243−14092861440m940474549+7516192768m109274267+…
3.由m(x+4+x6+x24+x31)=J(m(x)),设m(x)=4x+∑k=1∞xkuk,渐近展开:
m(x)=4x+16x7+64x275+384x31001+2560x411637+76800x5292843−716800x68813443−30105600x71962519689+342921600x8709670963+1028764800x928761656717−226328256000x106137702104697+…
4.极限值a0由下式求出:
m(an)−83ln(an)=n+4a0
5.关于bn渐近展开式计算:y=n1,X=23ln(n)+a0
F1=f(y,X)=y4+X+(b00+b01X)y+(b10+b11X+b12X2)y2+(b20+b21X+b22X2+b23X3)y3+(b30+b31X+b32X2+b33X3+b34X4)y4+(b40+b41X+b42X2+b43X3+b44X4+b45X5)y5+(b50+b51X+b52X2+b53X3+b54X4+b55X5+b56X6)y6+(b60+b61X+b62X2+b63X3+b64X4+b65X5+b66X6+b67X7)y7+(b70+b71X+b72X2+b73X3+b74X4+b75X5+b76X6+b77X7+b78X8)y8
F2=f(1+yy,X+23ln(1+y))
由F2=F1+4+F16+F124+F131求解得到:
b00=16−7,b01=83,b10=256−75,b11=41,b12=64−3,b20=6144−1295,b21=512123,b22=512−41,b23=1281,b30=163840−27387,b31=81922033,b32=1024−123,b33=204847,b34=2048−3,b40=1960800−2743793,b41=32768085369
b42=16384−2771,b43=16384797,b44=16384−103,b45=102403,b50=734003200−89215957,b51=3145728855727,b52=524288−118521,b53=39321634883,b54=262144−4603,b55=327680551,b56=16384−1,b60=41104179200−4615268183,b61=4587520013043753
b62=2097152−605645,b63=26214438351,b64=2097152−83575,b65=13107207731,b66=1310720−581,b67=2293763
类似于mathe提供的求解思路,我们来讨论稍一般的情形
对于an+1=an+ank−11
1.令ank=bn,得到
bn+1=bn+k+2bnk(k−1)+6bn2k(k−1)(k−2)+24bn3k(k−1)(k−2)(k−3)+120bn4k(k−1)(k−2)(k−3)(k−4)+720bn5k(k−1)(k−2)(k−3)(k−4)(k−5)+…
2.由m′−2k(k−1)ln(m′)=m+1−2k(k−1)ln(m)渐近展开:
m′=J(m)=m+1+2kmk−1−4k2m2k−1−24k3m3−5k2+2k3+3+48k4m46k+k4+4k3−14k2+3+480k5m5−73k4+50k3+13k5+100k2−75k−15−960k6m6325k3+50k2−248k4+17k6+6k5−135k−15+13440k7m71225k2−6125k3+2744k5−1441k6+1911k4+1470k+105+111k7+80640k8m8−32340k3−17052k4−13584k6−2652k7+43316k5+14700k2+6300k+997k8+315+161280k9m9102312k4−112896k5+42108k7−10721k8−12092k6+35280k3−35280k2+109k9−8505k−315+…
3.由m(x+k+2xk(k−1)+6x2k(k−1)(k−2)+24x3k(k−1)(k−2)(k−3)+120x4k(k−1)(k−2)(k−3)(k−4)+720x5k(k−1)(k−2)(k−3)(k−4)(k−5)+…)=J(m(x)),设m(x)=kx+∑k=1∞xkuk,渐近展开:
m(x)=kx+12kx1+2k2−3k+48kx27k3+13k−17k2−3+4320kx3−442k−1420k3+437k4+1490k2−67+2k5+12096kx4−6573k+42315k3−17661k2+7014k5−30072k4+4901+76k6+1209600kx5−117880k2+301049k4−151018k3+25666k6−160888k5+119816k+738k7−17483−4838400kx63163257k2+411621k4−2145479k3−35273k6+207669k5−2315013k−27849k7+738931+2136k8−203212800kx7−357561276k3−98841666k5+225077818k4−20753016k7+46893306k6+320183186k2+4159831k8−134911902k−37644k9+15791307+56k10+⋅
4.极限值a0由下式求出:
m(an)−2k(k−1)ln(an)=n+ka0
5.关于bn渐近展开式计算:y=n1,X=2(k−1)ln(n)+a0
F1=f(y,X)=yk+X+(b00+b01X)y+(b10+b11X+b12X2)y2+(b20+b21X+b22X2+b23X3)y3+(b30+b31X+b32X2+b33X3+b34X4)y4+(b40+b41X+b42X2+b43X3+b44X4+b45X5)y5+(b50+b51X+b52X2+b53X3+b54X4+b55X5+b56X6)y6+(b60+b61X+b62X2+b63X3+b64X4+b65X5+b66X6+b67X7)y7+(b70+b71X+b72X2+b73X3+b74X4+b75X5+b76X6+b77X7+b78X8)y8
F2=f(1+yy,X+2(k−1)ln(1+y))
由F2=F1+k+2F1k(k−1)+6F12k(k−1)(k−2)+24F13k(k−1)(k−2)(k−3)+120F14k(k−1)(k−2)(k−3)(k−4)+720F15k(k−1)(k−2)(k−3)(k−4)(k−5)+…求解得到:
b00=12k−(2k−1)(k−1),b01=2kk−1,b10=48k2−(7k−3)(k−1)2,b11=12k2(5k−4)(k−1),b12=4k2−(k−1),b20=4320k3−(k−1)(2k4+559k3−1221k2+659k+37),b21=24k3(12k−7)(k−1)2,b22=24k3−(13k−11)(k−1),b23=6k3k−1,b30=120960k4−(k−1)(76k5+15910k4−48812k3+46423k2−10298k−3011),b31=1440k4(k−1)(2k4+919k3−2151k2+1439k−173),b32=48k4−(49k−32)(k−1)2,b33=24k4(15k−13)(k−1),b34=8k4−(k−1)
b40=3628800k5−(k−1)(3334k6+511322k5−2033962k4+2779595k3−1359379k2+30191k+38659),b41=60480k5(k−1)(194k5+51077k4−162094k3+168236k2−54448k−2389),b42=1440k5−(k−1)(4k4+2573k3−6252k2+4573k−826),b43=144k5(241k−167)(k−1)2,b44=48k5−(33k−29)(k−1),b45=10k5k−1,b50=14515200k6−(k−1)(18908k7+2272111k6−11151258k5+19937499k4−14363838k3+637575k2+4729396k−2469193),b51=725760k6(k−1)(4498k6+816620k5−3312988k4+4761575k3−2695483k2+342545k+52993)
b52=120960k6−(k−1)(1138k5+363283k4−1181120k3+1295830k2−498998k+22747),b53=864k6(k−1)(4k4+3296k3−8199k2+6298k−1327),b54=576k6−(1403k−1009)(k−1)2,b55=240k6(177k−157)(k−1),b56=12k6−(k−1)