六阶模幻方
Tue, 14th January 2020Edit on Githubmodular
摘要
上的最优幻方
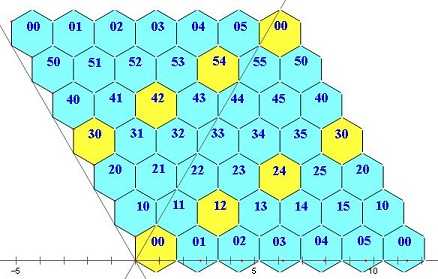
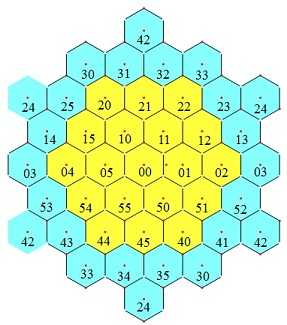
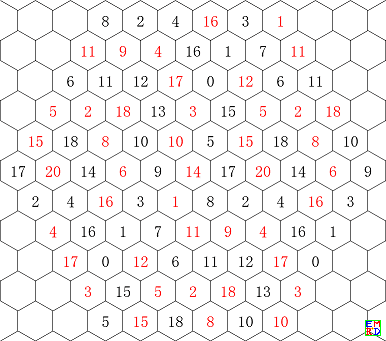
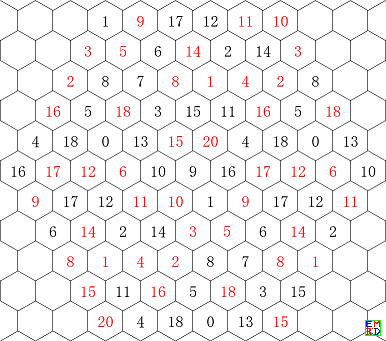
在编排6阶全对称幻方时,排成蜂窝状网格(又称为等距网格)比排成方格可体现更高的对称性,如图1所示。图中坐标相同的格为同一格,表现了所谓全对称幻方是嵌入到一个三维环面(轮胎面)的。在平面上表现时,可以按这个局部呈现的相邻关系扩展到整个平面上。扩展后,将视野取为一个如图2那样的正六角形区域时,呈现了6阶幻方的旋转对称性。在等距格网上,原来方格网上的一条对角线(x=y)看起来成为一条主轴。等距网格的对角线定义为相距次近的两格的连线,如图1中的黄色格列(在图2的正六角形视野中,呈现为正六角形的长对角线方向)。按此定义,6阶幻方有3条主轴方向和3条对角线方向,我们要求在其中的每一个方向上直线排列的6格数之和都等于幻方和数。这就比通常所谓的“全对称幻方”约束更多,对称性更高。
|
 |
|---|---|
| 图1 菱形视野 | 图2 六角形视野 |
用代数学的语言来描述,6阶幻方就是→{1, 2, 3, ..., 36}的一个映射f, f 满足某些函数方程,即幻方编排者所称的幻方律。比如关于行的幻方律即
(是36个填入数的平均值)
由于 f 的定义域为模, 所以这类幻方宜可称之为模上的幻方,简称模幻方。
除了定义时给出的2条幻方律(其实是6条,但是可用主轴线和对角线分别概括),6阶模幻方还有一些导出的幻方律,展现了其6阶旋转对称性。
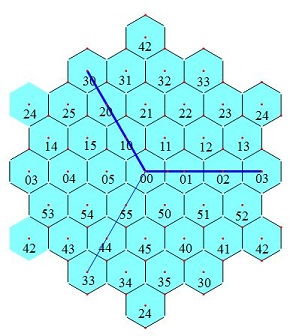
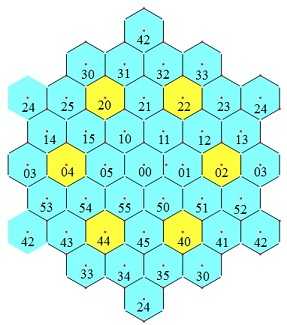
导出律1:对角线上的相间三格之和等于3A。如图3所示。变换视野,一条对角线的相间3格布成一个正三角形。图4显示两条这样的半对角线布成了一个正六角形,六角之和等于6A(导出律2)。 导出律3:见图5,4个黄色格(其中格33带红色纹线)之和等于4A。格33也可以在带纹线的青色格的位置,在此视野中这四格呈菱形。
 |
 |
|
|---|---|---|
| 图3 导出律1:对角线上的相间三格之和等于3A | 图4 导出律2:正六角形的六角之和等于6A | 图5 导出律3:边长为4格的菱形四角之和等于4A |
还有更多的表现6阶旋转对称性的导出律,下帖给出。这些导出律并非观察具体的数字而来,而是依据定义所给的约束方程消元而得。要用具体的数字来验证这些幻方律,我暂时还没有实例,因为我至今也没有编排出一个6阶模幻方的实例。事实上,对于这样的6阶幻方,用{1, 2, 3, ..., 36}是填不成功的。因为,图5中的4格减去图3中3格=4A-3A=A,所以A必须是整数。若用{1, 2, 3, ..., 36},总和Σ=18×37,A=Σ/36 非整数。
为了编出6阶模幻方,f 只能取其它的值域。为了保持幻方的数字之美,值域应该满足一定的要求。我们的要求是尽可能接近自然数前段{1~36}。由于18×37≡18(mod 36), 所以要使A为整数,最接近{1~36}的数组是从中去掉18,添上0,即{0~17,19~36}。
这就是本擂的目标:用{0~17,19~36}填入构建6阶模幻方。
更多规律分析
hujunhua接着给出了更多的规律分析 :
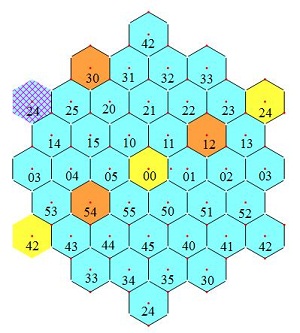
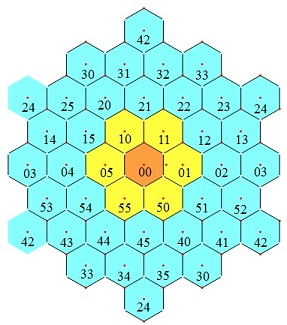
导出律4:如图6所示的边平行于主轴的最小正六角形(黄色格),六角之和加上中心格的2倍等于8A
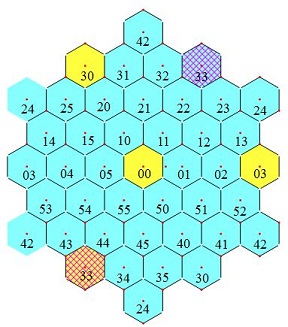
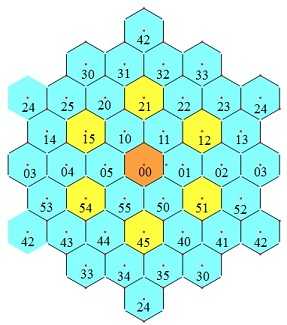
导出律5:如图7所示的边平行于对角线的最小正六角形(黄色格),六角之和减去中心格等于5A
 |
|
|---|---|
| 图6 导出律4 | 图7 导出律5 |
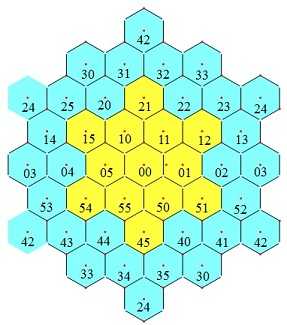
导出律6:图8所示正六角形区域的13个黄格之和等于13A. 由图6与图7叠加即得。 导出律7:图9所示正六边形区域的19个黄格之和等于19A. 由图8与图4叠加即得。 [attachimg]4355[/attachimg][attachimg]4356[/attachimg] 图8 导出律6 图9 导出律7
|
|
|---|---|
| 图8 导出律6 | 图9 导出律7 |
参数方案
接着hujunhua给出了参数方案分析 :
导出律1和导出律3涉及的格子少,导出律4涉及的格子密集,这很有利于手工得出参数解。图10就是一个在36个填入数之和为零(称为零和幻方)的条件下的参数布置方案。如果我们用填入数{±1, ±2, ±3, ..., ±18},就会产生零和幻方。
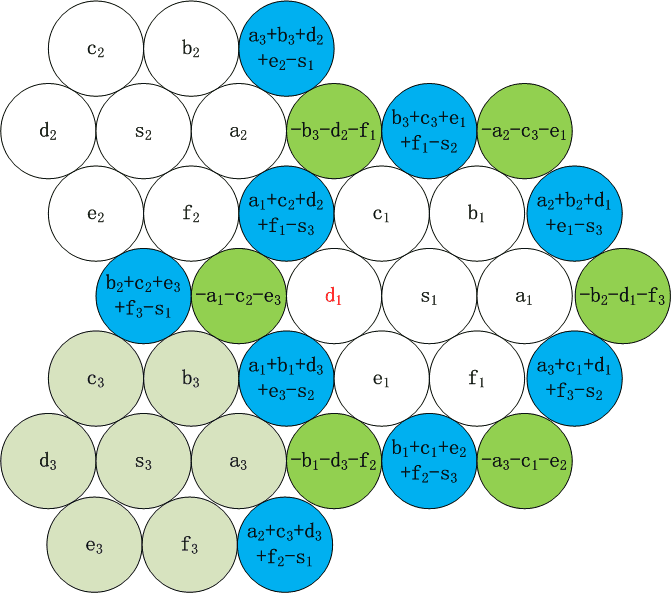
图10 参数解
6阶零和模幻方的定义中给出的36个约束方程的秩为24,所以参数解的维数为12. 上图中我们选两个白六角形的六个角a1,b1,...,f1, a2,b2, ..., f2为参数,其它格就可以由上述导出律得到。s1=-(a1+b1+...+f1)/2, s2=-(a2+b2+...+f2)/2, s3=-(s1+s2), a3=-(a1+a2),....
mathe后来也给出了类似的分析结果
单孔6阶模幻方不存在
hujunhua先开始用程序进行搜索 ,发现52小时才运行了大概5%的进度,没有找到任何合法的结果,终止了代码的运行。
mathe开始用C编写代码穷举,但是代码里面出现多次bug, 屡败屡战,终于穷举证明了只有一个空缺的6阶模幻方是不存在的 。
最小6阶模幻方
后来mathe的代码找到了3孔6阶模幻方 :
0~39:
Find:
| 第一列 | 第二列 | 第三列 | 第四列 | 第五列 | 第六列 |
|---|---|---|---|---|---|
| a_(0,0)=28 | a_(0,1)=7 | a_(0,2)=38 | a_(0,3)=8 | a_(0,4)=29 | a_(0,5)=10 |
| a_(1,0)=17 | a_(1,1)=25 | a_(1,2)=13 | a_(1,3)=22 | a_(1,4)=19 | a_(1,5)=24 |
| a_(2,0)=21 | a_(2,1)=18 | a_(2,2)=27 | a_(2,3)=15 | a_(2,4)=23 | a_(2,5)=16 |
| a_(3,0)=11 | a_(3,1)=32 | a_(3,2)=2 | a_(3,3)=33 | a_(3,4)=12 | a_(3,5)=30 |
| a_(4,0)=4 | a_(4,1)=35 | a_(4,2)=9 | a_(4,3)=37 | a_(4,4)=1 | a_(4,5)=34 |
| a_(5,0)=39 | a_(5,1)=3 | a_(5,2)=31 | a_(5,3)=5 | a_(5,4)=36 | a_(5,5)=6 |
Find:
| 第一列 | 第二列 | 第三列 | 第四列 | 第五列 | 第六列 |
|---|---|---|---|---|---|
| a_(0,0)=4 | a_(0,1)=3 | a_(0,2)=38 | a_(0,3)=22 | a_(0,4)=23 | a_(0,5)=30 |
| a_(1,0)=11 | a_(1,1)=35 | a_(1,2)=31 | a_(1,3)=8 | a_(1,4)=19 | a_(1,5)=16 |
| a_(2,0)=21 | a_(2,1)=32 | a_(2,2)=9 | a_(2,3)=5 | a_(2,4)=29 | a_(2,5)=24 |
| a_(3,0)=17 | a_(3,1)=18 | a_(3,2)=2 | a_(3,3)=37 | a_(3,4)=36 | a_(3,5)=10 |
| a_(4,0)=28 | a_(4,1)=25 | a_(4,2)=27 | a_(4,3)=33 | a_(4,4)=1 | a_(4,5)=6 |
| a_(5,0)=39 | a_(5,1)=7 | a_(5,2)=13 | a_(5,3)=15 | a_(5,4)=12 | a_(5,5)=34 |
hujunhua将它们转化为图案后发现它们其实是等价的

mathe还验证 了也不存在双孔6阶模幻方,并且穷举出所有可能的三孔6阶模幻方 。
美图秀
hujunhua首先对数据进行了分析处理,得出 :
把数据平移为-19~+19后,发现大部分都是正负对称的,即都缺 0,剩下的两洞对称。
我还没有发现缺奇数的,目前只发现缺±2、±4、±6、±8、±10、±12、±14、±16的。
相反数对的分布有中心对称、旋转对称、镜像对称、分块对称和不对称的。
不对称的只有少数.
数据预处理完成(转化为M10规则表), 去重前的分类统计结果:
{0~38}的48个,化为{-19~19}后全都为非对称数组(即都不含0洞)。
{洞组, 频数}如下:
{{-18, -12, -6}, 24},
{{-16, -14, -6}, 12}
{{-14, -12, -10},12}。
可见皆为非零和幻方,总和为36。化为零和幻方,每格-1,成为{-20~18},倒是全部为奇数洞了。
{1~39}的6792个,化为{-19~19}后,全部为零和幻方,其中6624个为对称数组,其余168个为非对称数组(含0)。
{洞组, 频数}
{{-2, 0, 2}, 180},
{{-4, 0, 4}, 240},
{{-6, 0, 6}, 972},
{{-8, 0, 8}, 540},
{{-10, 0, 10}, 768},
{{-12, 0, 12}, 888},
{{-14, 0, 14},312},
{{-16, 0, 16}, 780},
{{-18, 0, 18}, 1944},(\times 这个洞组的最多,先前104例中居然没碰到\times )。
{{-10, -8, 18}, 36},(\times 非对称洞组\times )
{{-18, 8, 10}, 36},(\times 与上行对称,重合情况有待分析\times )
{{-10, -6, 16}, 12},
{{-16, 6, 10}, 12}, (\times 与上行对称,重合情况有待分析\times )
{{-14, -4, 18},36},
{{-18, 4, 14}, 36}}(\times 与上行对称,重合情况有待分析\times )
按洞组分离后,就有利于去重了。(免于在不同洞组间进行比较)
手工处理了48个{0~38}的去重,结果只有4个本原解。每个本原解重复12次(含自身)。
把数组化成了{-20~18}, 使总和为0,相应的{洞组, 本原解数}如下:
{{-19, -13, -7}, 2}
{{-17, -15, -7}, 1}
{{-15, -13, -11}, 1}
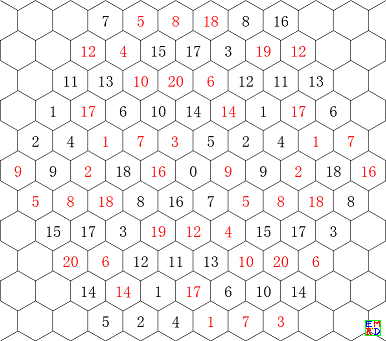
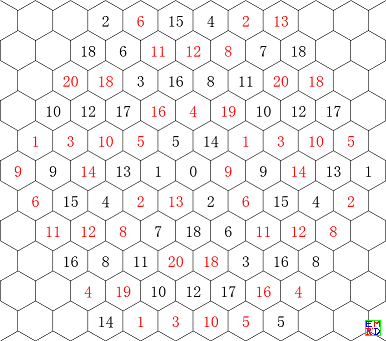
然后他设计了一个画图的mathematica代码
RulesArray =Solve[x + y + z == 15 && 0 <= x <= 10 && 0 <= y <= 10 && 0 <= z <= 10, {x, y, z}, Integers];
mf[n_] := m13906[[n, Mod[5 - z, 6, 1], Mod[y + 1, 6, 1]]]
Graphics3D[{Sphere[{x, y, z}], Text[Style[Abs@mf[100], Medium, Bold, If[mf[100] > 0, Black, Red]], {x, y, z}]} /. RulesArray, ViewPoint -> {100, 100, 100}, Boxed -> False]可以给出类似如下的图 :
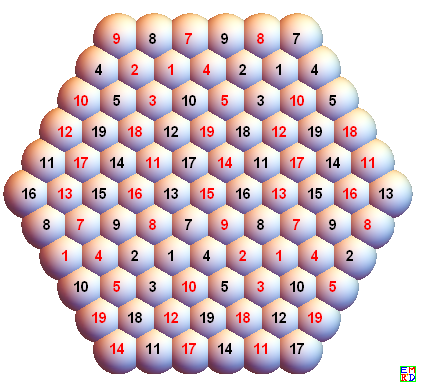
程序中的坐标{5-z,y+1}的选择是为了使画出来的图的左上角幻方与 mathe 的解的排列顺序一致。
坐标使用±{-x, y}, ±{-y, x}, ±{-y, z}, ±{-z, y}, ±{-z, x}或±{-x, z}都是可以的,无非是旋转和镜像的关系。
或者在此基础上再加一个常数也行(比如我们用的+5和+1),这是平移。
画法原理:就是在平面 x+y+z=15 的下图所示整点上画单位球,利用球的相贯线自动形成蜂巢状。
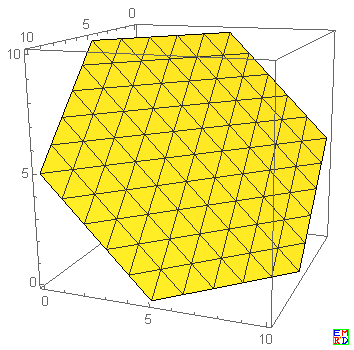
于是他继续分析余下数据,并给出如下图解:
{{-10, -8, 18}, 36}
{{-18, 8, 10}, 36}
两组正负对应重复,共有3个本原解,每解重复24次。旋转6X转置2X正负2.



{{-10, -6, 16}, 12},
{{-16, 6, 10}, 12}
两组正负对应重复,共有1个本原解,重复24次。

{{-14, -4, 18},36},
{{-18, 4, 14}, 36}}
两组正负对应重复,共有3个本原解,每解重复24次。



最后剩下6624个{1~39}对称洞组的
{洞组, 频数}
{{-2, 0, 2}, 180},
{{-4, 0, 4}, 240},
{{-6, 0, 6}, 972},
{{-8, 0, 8}, 540},
{{-10, 0, 10}, 768},
{{-12, 0, 12}, 888},
{{-14, 0, 14}, 312},
{{-16, 0, 16}, 780},
{{-18, 0, 18}, 1944}
注意到其中有些频数不是24的倍数,所以不可能都是每解24重。
失重的应该是正负对称,那些中心对称、镜像对称和平移对称的可能会正负失重,因为它们是自对称的。
所有频数都是12的倍数,由于不存在旋转和转置自对称者,故可预料每解至少12重。
{{-2, 0, 2}, 180}去重:
mathe是固定 a(3, 2)=2,化为对称数组后即红18不动。下面画图时,a(3, 2)位于中心。
去掉旋转和镜像重复后得15个解 ,它们的相反数对全都是平移对称的,因此没有取反重复,故此即本原解。

{{-4, 0, 4}, 240}去重,16个本原解
先按上述方法去掉镜像和旋转重复,得20解

审核这20解的取反重复,发现3、6、7、8、10、11、12、15、16、17、19、20 这 12 个的相反数对是平移对称的,因此是取反自对称的。
1 与 9,2 与 18, 4 与 13, 5 与14 是取反重复的。
4与13, 5与14 的相反数对关系很诡异,即我前面所称的分块对称,其实这四个貌似也有某种取反自对称。
中心对称12图
mathe 给的3孔数组幻方中,第1个就是中心对称幻方(见27楼和34楼),所以最初以为会有很多中心对称幻方的。
没想到最终只有12个。不多则可以全列出来了。

去重汇总
一、6624个对称数组去重结果汇总:
| 洞组 | 频数 | 去旋转和镜像 | 取反平移对称 | 取反中心对称 | 取反对称对 | 本原解数 |
|---|---|---|---|---|---|---|
| {-2,0,2} | 180 | 15 | 15 | 0 | 0 | 15 |
| {-4,0,4} | 240 | 20 | 10 | 0 | 5对 | 15 |
| {-6,0,6} | 972 | 81 | 37 | 6 | 19对 | 62 |
| {-8,0,8} | 540 | 45 | 7 | 0 | 19对 | 26 |
| {-10,0,10} | 768 | 64 | 14 | 0 | 25对 | 39 |
| {-12,0,12} | 888 | 74 | 49 | 1 | 12对 | 62 |
| {-14,0,14} | 312 | 26 | 20 | 2 | 2对 | 24 |
| {-16,0,16} | 780 | 65 | 29 | 0 | 18对 | 47 |
| {-18,0,18} | 1944 | 162 | 87 | 3 | 36对 | 126 |
| 合计 | 6624 | 552 | 268 | 12 | 136对 | 452 |
二、非对称数组,7个本原解,
所以共是459个本原解。其中取反自对称的为280个.
不对称的种种(一)
对称幻方虽然多,模式就那两种。不对称的可以想像必是各种各样了。
如何表征、识别各种不对称呢?为了使用程序处理,我们找的是相反数对的中点。
设#是幻方 x 中的一个数,通过计算Position(x,#)+Psition(x,-#)(mod 6)搜索生成中点表.
然后累计各中点被搜到的次数,形成权数表。显然权数之和为18.
排序后的权数表就成为幻方相反数对的分布特征。
两个不同对称分布的幻方,权数表可能不一样,而两个不同权数表的幻方,肯定有不同的对称分布。
例如:中心对称幻方的权数表为{18}, 平移对称幻方的权数表为{2, 2, 2, 2, 2, 2, 2, 2, 2}.
注意我们计算中点坐标时没有除以2,而模仍然取的是6。原因如下:
如34#所示,由于周期性,每对相反数实际上有4个中点,这4个中点扩展铺开形成的网格周期为3。
因此如果中点坐标不除以2,则把这四个中点的权数合并(视为同一个)时需要取模6.
以下是M10程序生成的去掉旋转和镜像重复和平移对称后的282个本原解的权数表的频数。
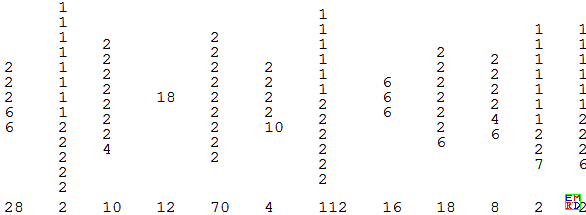
我们看到有3个权数表的频数为2,表明按这种对称分布的幻方各只有一对(取反重复)。
权数表最短的{18},显然就是中心对称的了。
权数表为{6,6,6}的就是所谓“镜像对称”。
权数表为6个2并6个1的频数最大,达112,表明这是一种典型分布,虽不如中心对称和平移对称简单,应该也是一种很有规律的分布。
权数表为9个2的与平移对称的权数表一样,但显然两者不同。说明权数表有丢失信息,可能合并了不同的分布细类。
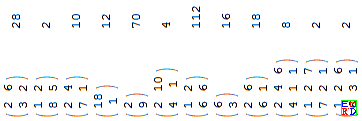 中点权数表的合并横放版
中点权数表的合并横放版
不对称的种种(二)
既然中点权数表不能完全区分幻方相反数偶的分布,我们再寻找一种表征:向量表。
#是幻方 x 中的一个数,相反数偶的向量= Position(x, #)-Position(x, -#)(mod 6, -2)
注:(mod 6, -2)表示取模6的绝对值最小剩余,即剩余系取 {-2, -1, 0, 1, 2, 3).
统计向量权重时,方向相反的等长向量合并计权,然后将所得权重除以2。
去除旋转和镜像对称后的552个幻方的相反数偶向量表统计频数如下:

显然,{向量, 权重} 表最短的{{3, 0}, 18}即平移对称幻方,它的18个相反数偶向量均相同。
程序计算结果中,包括{{3, 0}, 18} 和 {{3, 3}, 18}两种形式,实为同一种分布,旋转120°而已。
程序并不排除{{0, 3}, 18}, 但却没有发现,那就是竟然在旋转、镜像去重中都滤掉了。
那个频数为12的{向量, 权重} 表,即属中心对称幻方。
不对称的种种(三)
从中点权重表与相反数偶向量表的频数并不能一一对应。
已经验证的一一对应关系有三项:
1、平移对称
2、中心对称
3、频数为112者,说明这种不再细分了。
剩下的向量表有一个频数为72,超过了剩下的中点权重表中的最大频数。可见向量表也不能完全区分相反数偶的分布。
也许把两都交叉起来,就比较确定了。