钝角三角形的概率

Thu, 30th January 2020Edit on Github概率三角形正方形

倪举鹏于14年1月份提问:
54张牌,地主里面，地主得到20张牌，那么地主得到炸弹的概率是多少（得到4个一样或者对王）?

wayne快速给出了答案，然后他们引申出了平面图形中随机选择三个点，构成钝角三角形的一系列概率问题.

扑克牌问题

对于扑克牌问题，wayne首先计算出三个人都没有炸弹的概率:
1）计算54张牌分成17,17,20三堆，且不存在4条和对王的所有情况：
母函数 $((x+y+z)^4-x^4-y^4-z^4)^{13} ((x+y+z)^2-x^2-y^2-z^2 )$ 的 $x^{20}y^{17}z^{17},x^{17}y^{20}z^{17},x^{17}y^{17}z^{20}$ 的系数。

Select[CoefficientRules[((x+y+z)^4-x^4-y^4-z^4)^13 ((x+y+z)^2-x^2-y^2-z^2 ),{x,y,z}],Min[#[[1]]]==17&&Max[#[[1]]]==20&]

算得 $341495369180333055148032\times 3= 1024486107540999165444096$
2）计算54张牌分成17,17,20三堆的所有可能情况：Multinomial[17, 17, 20] =749991557119474188218700
3）有炸弹的概率就是：
$1-\frac{341495369180333055148032}{749991557119474188218700}=\frac{79350463857642022741}{145686005656463517525} \approx 0.5446677153$
所以有54.5%的概率至少有一人出现炸弹。并且给出了模拟结果:
123
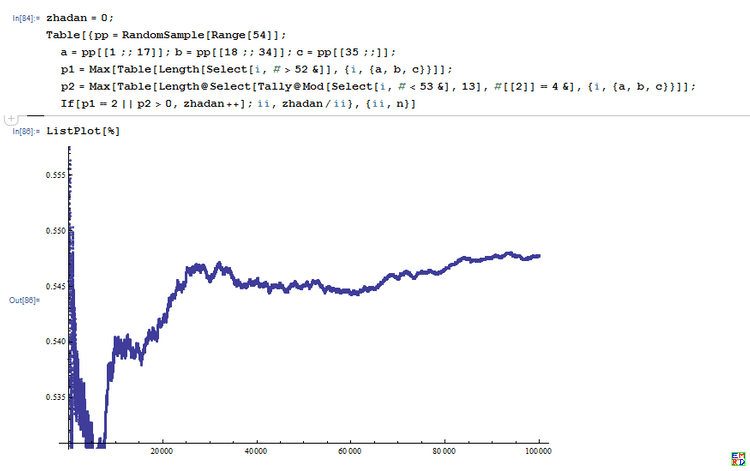
从54张牌里随机取20张出来，没有炸弹(4条或对王)的概率：
$((x+1)^4-x^4)^13 ((x+1)^2 -x^2)$ 中 $x^{20}$ 的系数 223786474655744 除以 $C_{54}^{20}$ .
于是有炸弹的概率： $1- \frac{223786474655744}{321387366339585} =\frac{1072537271251}{3531729300435}\approx 0.303686$ .
模拟结果:
321

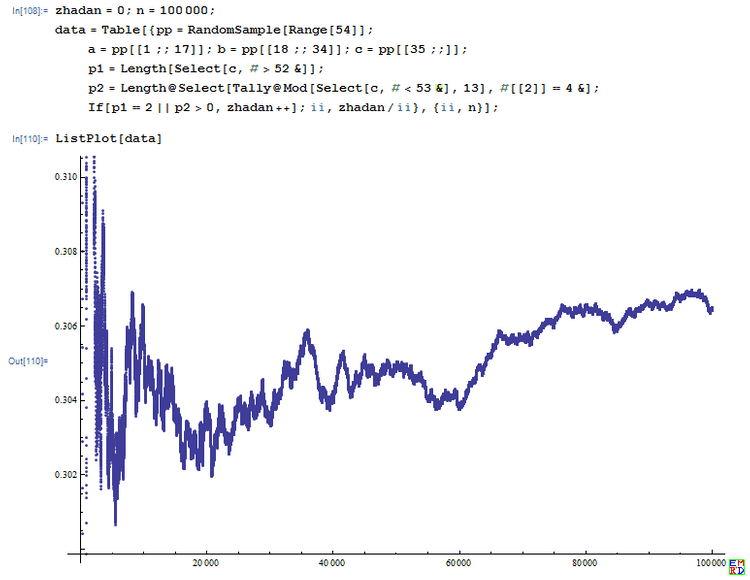
钝角三角形概率问题

倪举鹏由此引申出一个扩展的问题:
随机给定一个三角形，是钝角三角形的概率是多少？wayne指出结果依赖于三个点的限定区域

圆周问题

圆周上随机选择三点构成钝角三角形的概率是多少呢？ Lwins_G认为还可以推广到“在超球面 $S_n$ 上任意取 $k$ 个点，求这 $k$ 个点可以被全部分配在半个超球面上的概率”。
sheng_jianguo给出如下的解答:
因为是均匀分布，所以取到每个点的概率密度与取到其对径点的概率密度是一样的。每个点都有一个对径点，这样便有 $k$ 对点。在每对点中各取一点，共有 $2^k$ 中取法，每种取法的概率密度是相同的。现在只要计算这 $2^k$ 种取法中，有多少种取法(记为 $F(k)$ )是落在同一半球上的，则所求概率为 $\frac{F(k)}{2^k}$ 。
上面有个假设，即认为 $F(k)$ 的值只与 $k$ 有关，而跟 $k$ 个点的具体位置无关。这个是可以证明的（忽略两点重合，三点共大圆的零概率情况）。而且，还可以证明， $F(k)$ 等于球面上 $k$ 个大圆（任意两个大圆不重合，任意三个大圆不共点）把球面分割成小片的片数。这个数目等于 $k^2-k+2$ 。
于是三维球面情况所求概率等于 $\frac{k^2-k+2}{2^k}$ 。
hujunhua给出了对应的二维情况的图解：
在一个圆周上随机取3点，构成钝角三角形的概率为3/4. 计算方法可以不用积分，使用sheng_jianguo的方案即可:
twodcircle
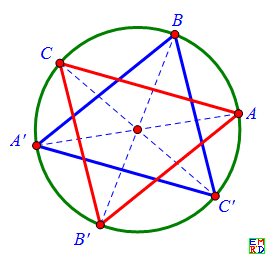
随机取三点，再考虑其对径点，取点或其对径点的概率是相同的，共有8个三角形，只有图中的2个才是锐角三角形，其它6个都是钝角三角形。
并且进一步给出:
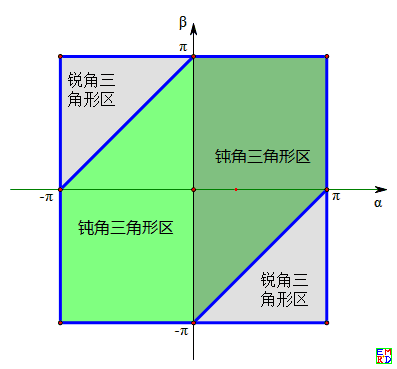
如下图1，当 $0\lt \alpha\lt \pi$ 时（黑标记角）, 点B位于OA弧的对顶角弧上时才是锐角三角形，这时 $-\pi\lt\beta\lt\alpha-\pi$ ，对应下图2右下角的灰色三角区。在其它位置都是钝角三角形，对应于下图2中的深绿色区。
当 $\pi\lt\alpha\lt0$ 时（红标记角）, 点B同样位于OA弧的对顶角弧上时才是锐角三角形，这时 $\pi+\alpha\lt\beta\lt\pi$ ，对应于下图2左上角的灰色三角区。在其它位置都是钝角三角形，对应于下图2中的浅绿色区。
钝角区
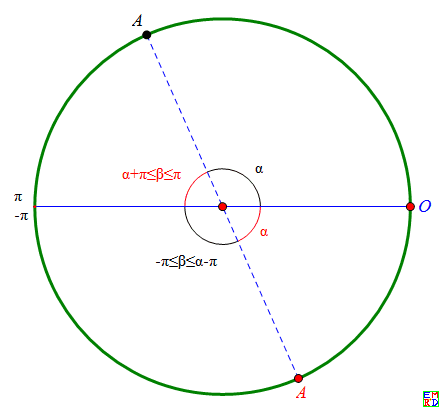
kastin基于三个点的不同分布概率，使用积分模型也给出了很多不同的结论。
mathe给出了一种通过积分计算的方案:
圆周上随机取n个点，落在半圆上概率可以如下计算。
对于任意t, $0\lt t\le\frac12$ ,我们设n个点落在角度不超过 $t\times 2\pi$ 上概率为 $F_n(t)$ ,于是我们知道 $F_2(t)=2t$ .
而且 $F_{n+1}(t)=\int_{s=0}^t (2t-s)dF_n(s)$ .
然后 $F_n(\frac12)$ 就是所求的结果.
比如:
$F_3(t)=\int_{s=0}^t(4t-2s)ds=3t^2$ ,
$F_4(t)=\int_{s=0}^t(2t-s)\times 6sds=4t^3$ .
猜测 $F_n(t)=nt^{n-1}$ ,于是 $F_{n+1}(t)=\int_{s=0}^t (2t-s)\times n(n-1)s^{n-2}ds=\int_{s=0}^n(2n(n-1)ts^{n-2}-n(n-1)s^{n-1}ds=2nts^{n-1}-(n-1)s^n|_{s=0}^t=(n+1)t^n$ ,归纳假设成立.
于是n个点落在半圆上概率为 $\frac n{2^{n-1}}$ .
对于这种情况，hujunhua也用他的方法得出相同的结果:
圆周上任取n点偏于一个半圆的概率，可以如下计算：
首先，不用考虑其中任意两点处于一种固定的相对位置的情况，比如两点重合或者处于对径位置情况。对于连续的圆周来说，这样的特例概率是零。所以只需要考虑n个不同点，并且没有两点处于对径位置的情况，这样的一个n点组，我们称为一个样本。
任一特定样本s，将其中的1个点或者更多的点换成其对径点所得的新样本 s’ 称为它的一个相关样本。显然，s 连同它自身共有 $2^n$ 个相关样本，对于对径变换，它们组成一个封闭的簇。
于是整个样本空间可以划分为一个个簇, 所有的簇组成样本空间的一个商集。显然，每个簇恰好有2n个半偏样本，所以取到半偏样本的概率是 $\frac{2n}{2^n}=\frac{n}{2^{n-1}}$ .
关于每个簇恰好有2n个半偏样本，说明一下。一个簇有2n点，分为n对对径点，将圆周分成了n对相对弧段。在任意一段半圆周上，都恰好包含其中的n个点（直径端无点）或者n+1个点（直径端有点，我们不用考虑这种零概率情况），这就是一个半偏样本。当半圆的直径端在一对相对弧段上滑动时，所包含的半偏样本是不变的，所以一对相对弧段对应于1对半偏样本。故共有n对半偏样本。
n点偏于半圆周
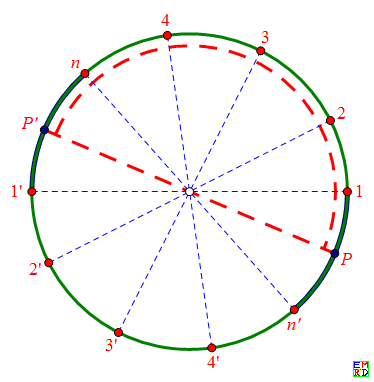
如图，红色虚线半圆（为了清晰，将它缩到了圆内，实际上应该与圆重合的）包含了一个半偏样本｛1,2,3,4,..., n｝,当半圆的直径端P,P'在相对弧段1n', 1'n上滑动时，半圆弧所包含的点仍然是{1,2,3,4, n}. 所以相对弧段1n'&1’n 就对应于一对相对的半偏样本｛1,2,3,4,...,n｝&｛1',2,',3,',4',...,n'｝.

sheng_jianguo进一步将问题推广到高维：
若在 $r+1$ 维空间中， $n$ 个 $r-1$ 维超球面最多可以把 $r$ 维超球面切割成 $F(n,r)$ 部分，则当 $r$ 为奇数时 $F(n,r)= 2\binom{n}{1}+2\binom{n}{3}+\dots+2\binom{n}{r}$ 当 $r$ 为偶数时 $F(n,r)= 2\binom{n}{0}+2\binom{n}{2}+\dots+2\binom{n}{r}$ （其中， $\binom{n}{i}=\frac{n!}{i!\cdot{(n-i)!}}$ 表示 $n$ 个数中取 $i$ 个数组合的个数 $(i=0,1,2,\dots,r)$ ，当 $n\lt r$ 时， $\binom{n}{i}=0$ ). 所以，若在 $r+1$ 维空间中，在 $r$ 维超球面上任意取 $n$ 个点，则这 $n$ 个点可以被全部分配在半个超球面上的概率为 $p=\frac{F(n,r)}{2^n}$ 。请各位高手看看上面组合公式是否还能简化。举例：当 $r=1$ 时，即2维空间中， $n$ 个双点（0维球面）最多可以把圆（1维球面）分为 $F(n,1)=2\binom{n}{1}=2n$ ，故 $r=1$ 时, $p=\frac{2n}{2^n}$ 。当 $r=2$ 时，即3维空间中， $n$ 个圆（1维球面）最多可以把球面（2维球面）分为 $F(n,2)=2\binom{n}{0}+2\binom{n}{2}=n^2-n+2$ 部分，故 $r=2$ 时， $p=\frac{n^2-n+2}{2^n}$ 。当 $r=3$ 时，即4维空间中， $n$ 个2维球面最多可以把3维球面分为 $F(n,3)=2\binom{n}{1}+2\binom{n}{3}=\frac{n^3-3n^2+8n}3(n>2时)$ 部分，故 $r=3$ 时， $p=\frac{n^3-3n^2+8n}{3\cdot{2^n}}$ ，当 $n\gt 2$ 时， $p=1$ ，当 $n\lt 3$ 时。

正方形情况

那么在单位正方形内,随机取三点,构成三角形是钝角三角形的概率为多少?
wayne发现百度贴吧里面已经有人通过复杂的符号计算得出了结果 $\frac{97}{150}+\frac{\pi}{40}\approx0.72520648300641149763$ 并且这个结果和他的数值模拟结果非常匹配。
Lwins_G给出:
简要思想是：

一个角是否为钝角，可以用形成该角的两条有向边的内积（有向边看作向量）的正负来判别。
一个三角形为钝角三角形，当且仅当其恰好有一个钝角。
故而，这归结为计算
$3 \int_0^1 \int_0^1 \int_0^1 \int_0^1 \int_0^1 \int_0^1 f((x_2 - x_1)(x_3 - x_1) + (y_2 - y_1)(y_3 - y_1)) dx_1 dy_1 dx_2 dy_2 dx_3 dy_3 .$
其中 $f(x)$ 当 $x \lt 0$ 时取 $1$ ，否则取 $0$ 。

从而验证了百度贴吧中结果的正确性。