超立方体中的最大立方体

Mon, 28th October 2019Edit on Githubbubbles

zhouguang 提出了一个关于超立方体的最大嵌套问题:
设d(m,n)表示在单位n维方（n为1、2、3时，分别对应线段、正方形、立方体）中的最大的m维方的大小（这个大小在m为1、2、3时，分别对应长度、面积、体积，并且此处m不大于n）。求d(m,n)。

他首先给出: 对于一些简单的情况，已知如下结果：
1、d(k,k)=1；
2、d(1,k)=k\sqrt{k}，均为体对角线的长度；
3、d(2,3)=98\frac 98，d(2,3)表示单位立方体内能够容纳的最大正方形的面积。
大家还能算一些其它的d(m,n)的值么？

补充内容 (2018-9-4 09:53):
补充m为2时的情况：
4、d(2,2k)=k，当n为偶数时，最大正方形的对角线和n维方的主对角线（体对角线）重合。
5、d(2,2k+1)=k+18\frac 18，当n为奇数时，最大正方形的顶点在某条棱的14\frac 14处。

这个问题非常复杂，zhouguang, wayne, zgg__, mathe等参与了讨论，最终我们解决了m=3的情况，即解决了在单位n维方种能够嵌入的最大的三维立方体。

详细内容

为了解决 d(3,4)，zhouguang写了一段mathematica代码用一个三维超平面去截取一个四维超立方体获取对应的三维交集对象

ll[p1_, p2_] := Dot[p1 - p2, p1 - p2];
cr[l_, s_, t_] := Module[{p1 = First[l], p2 = Last[l], x},
   If[s.p1 != s.p2, x = (s.p2 - t)/(s.p2 - s.p1); If[0 <= x <= 1, Return[x p1 + (1 - x) p2], Return[0]],  Return[0]];];
dr[ps_] := Module[{ss, pn, q, x, y, ans, i},
   If[Length[ps] <= 3, Print["Err Short"]];
   ss = {{0, 0, 0}, {0, Sqrt[ll[ps[[1]], ps[[2]]]], 0}};
   pn = {x, y, 0};  q = Map[ll[pn, #] &, ss] == Map[ll[ps[[3]], #] &, Take[ps, 2]];
   AppendTo[ss, pn /. Last[Solve[q, {x, y}]]];
   Do[pn = {x, y, z};   q = Map[ll[pn, #] &, ss] == Map[ll[ps[[i + 4]], #] &, Take[ps, i + 3]];
    ans = Solve[q, pn]; If[Length[ans] < 1, Print["Err"];];
    AppendTo[ss, pn /. Last[ans]];
    , {i, 0, Length[ps] - 4}]; ss];
pcs = (Table[IntegerDigits[i, 2, 4], {i, 0, 15}] 2 - 1)/2
pcs // Length
ls = Select[Subsets[pcs, {2}], ll[First[#], Last[#]] == 1 &];
ls // Length

然后把图做出来，比如
tesseract1
tesseract2
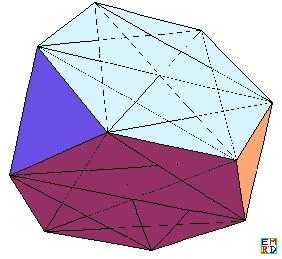
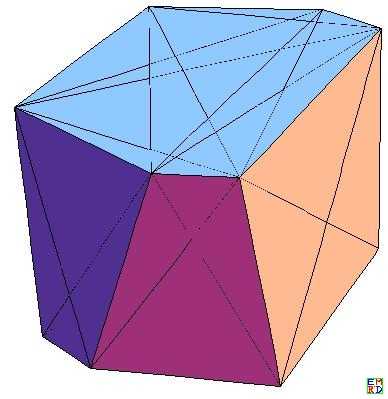
然后他在上面第二个图得出一个边长为1.0074347568842812，得出d(3,4)≥1.02247050844335d(3,4)\ge 1.02247050844335。
接下去他分析认为d(3,5)=342−273=1.31789d(3,5)=34\sqrt{2}-27\sqrt{3}=1.31789。其中对应立方体的八个顶点分别为：(1212−t−t1212−t12−t12−t−t121212−t12−t1212tt−12−12−12t−12t−12−12−12−12tt−12−12t−12t−12)\begin{pmatrix}\frac12&\frac12&-t&-t&\frac12\\ \frac12&-t&\frac12&-t&\frac12\\ -t&-t&\frac12&\frac12&\frac12\\ -t&\frac12&-t&\frac12&\frac12\\ t&t&-\frac12&-\frac12&-\frac12\\ t&-\frac12&t&-\frac12&-\frac12\\-\frac12&-\frac12&t&t&-\frac12\\-\frac12&t&-\frac12&t&-\frac12 \end{pmatrix}，其中t=3−62=0.275255t=\frac{3-\sqrt{6}}2=0.275255.
并且他给出对应的下图 tesseract3

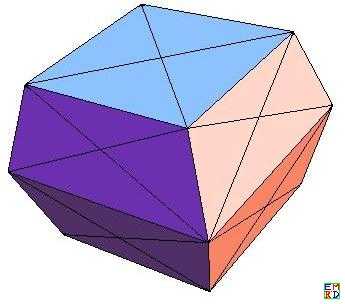
继续计算他得出如下表格:

d(m,n) m=1 m=2 m=3 m=4 m=5 m=6
n=1 1 - - - - -
n=2 1.414213562 1[/td][td]- - - -
n=3 1.732050808 1.125 1 - - -
n=4 2 2 1.022470508 1 - -
n=5 2.236067977 2.125 1.317889316 1 -
n=6 2.449489743 3 2.828427125 1
n=7 2.645751311 3.125 2.828427125
n=8 2.828427125 4 3.267669390
n=9 3 4.125
n=10 3.162277660 5

但是接下去zgg__得出了d(3,7)更好的结果d(3,7)=2.892895457:

mm = {{-a, 1/2, -d, -(1/2), -(1/2), -(1/2), -(1/2)}, {1/2, -b, c, -(1/2), -(1/2), -(1/2), -(1/2)}, {c, -b, 1/2, -(1/2), -(1/2), 1/2, 1/2}, {-d, 1/2, -a, -(1/2), -(1/2), 1/2, 1/2}, {-c, b, -(1/2), 1/2, 1/2, -(1/2), -(1/2)}, {d, -(1/2), a, 1/2, 1/2, -(1/2), -(1/2)}, {a, -(1/2), d, 1/2, 1/2, 1/2, 1/2}, {-(1/2), b, -c, 1/2, 1/2, 1/2, 1/2}};
ll[p1_, p2_] := Dot[p1 - p2, p1 - p2];
c[x_, y_] := ll[mm[[x]], mm[[y]]];
e1 = {c[1, 2], c[2, 3], c[3, 4], c[4, 1], c[5, 6], c[6, 7], c[7, 8], c[8, 5], c[1, 5], c[2, 6], c[3, 7], c[4, 8]};
e2 = {c[1, 6], c[2, 5], c[3, 8], c[4, 7], c[1, 8], c[4, 5], c[2, 7], c[3, 6], c[1, 3], c[2, 4], c[5, 7], c[6, 8]};
e3 = {c[1, 7], c[2, 8], c[3, 5], c[4, 6]};
e = Join[Map[# - z &, e1], Map[# - 2 z &, e2], Map[# - 3 z &, e3]];
ans = Solve[e == 0, {a, b, c, d, z}][[3]];
ans // N // MatrixForm
zz = RootReduce[Sqrt[z /. ans]];
f = First[zz][x]
N[zz^3, 10]

然后mathe使用拉格朗日乘数法验证了zhouguang的d(2,n)的结论并且尝试把方法推广到d(3,n) 然后他把问题转化为求一个m×nm\times n阶矩阵问题:
我们可以对坐标进行平移，使得外面的n维超立方体中离里面m维超立方体一个顶点A最接近的顶点坐标为(0,0,...,0)(0,0,...,0),最远顶点坐标为(1,1,...,1)(1,1,...,1)
这时设A(a1,a2,...,an)A(a_1,a_2,...,a_n), 和A有边相连接的m条边为Xh(a1+th1,a2+th2,...,an+thn)X_h(a_1+t_{h1},a_2+t_{h2},...,a_n+t_{hn})
于是对于任意i,有∑h=1mthi=1−2ai\sum_{h=1}^m t_{hi}=1-2a_i,以及边界条件∑{h∣thi≥0}thi≤1−ai=1+∑h=1mthi2,∑{h∣thi≤0}thi≥−ai=∑h=1mthi−12\sum_{\{h|t_{hi}\ge 0\}}t_{hi}\le 1-a_i=\frac{1+\sum_{h=1}^mt_{hi}}2, \sum_{\{h|t_{hi}\le 0\}}t_{hi}\ge -a_i=\frac{\sum_{h=1}^mt_{hi}-1}2
或者说∑{h∣thi≥0}thi−∑{h∣thi≤0}thi≤1\sum_{\{h|t_{hi}\ge 0\}}t_{hi}-\sum_{\{h|t_{hi}\le 0\}}t_{hi}\le 1,即∑h=1m∣thi∣≤1\sum_{h=1}^m |t_{hi}|\le 1 （取最大值时，这n个不等式应该大部分会变为等式)
以及对于任意h,有∑i=1nthi2\sum_{i=1}^n t_{hi}^2都相等（要求等于1m∑i=1n(1−2ai)2=1m∑i=1n(∑h=1mthi)2)\frac 1m\sum_{i=1}^n (1-2a_i)^2=\frac 1m\sum_{i=1}^n (\sum_{h=1}^mt_{hi})^2)
还有对于任意不同的h1,h2h_1,h_2,有∑i=1nth1ith2i=0\sum_{i=1}^n t_{h_1i}t_{h_2i}=0
而我们的目标是让∑i=1nthi2\sum_{i=1}^n t_{hi}^2或∑i=1n(1−2ai)2=∑i=1n(∑h=1mthi)2\sum_{i=1}^n (1-2a_i)^2=\sum_{i=1}^n (\sum_{h=1}^mt_{hi})^2最大化.
为了得到最大值解，我们除了使用(m+2)(m−1)2\frac{(m+2)(m-1)}2组已知的二次等式约束，以及上面n组不等式的部分改为等式的表达式外，另外选择若个独立的thit_{hi}将它们变为0来求得可能的最优解
我们可以查看m×nm \times n阶矩阵
T=(t11t12...t1nt21t22...t2n............tm1tm2...tmn)T=\begin{pmatrix}t_{11}&t_{12}&...&t_{1n}\\t_{21}&t_{22}&...&t_{2n}\\...&...&...&...\\t_{m1}&t_{m2}&...&t_{mn}\end{pmatrix}
于是要求矩阵各行的元素平方和都相同，不同两行之间内积为0（也就是行向量长度都相等而且两两正交）。
而任意一列中数字的绝对值之和不超过1.
得到任意这样的矩阵，我们就可以构造出满足条件的超立方体。而上面构造的目标是使得行向量长度尽量大。
由于最大值必然在所有变量的边界条件取到，所以如果矩阵中一个数字不是0，那么所在列所有非零数字绝对值之和必须为1，由此得出最优解任意一列数字绝对值之和为一。
由此可以得到矩阵中非零数字数目最多是(m+2)(m−1)2+n\frac{(m+2)(m-1)}2+n个。

比如用这种方法计算d(3,4)
首先我们需要列出所有列绝对值和为1，行之间正交，而且所有行向量长度相同的潜在的不等价3×43\times 4矩阵（交换两行或两列得出的矩阵认为是等价）本质上只有四种:
(−ad1−g1b−eg01−a−b1−d−e00)\begin{pmatrix}-a & d& 1-g& 1\\b& -e&g & 0\\1-a-b&1-d-e&0&0\end{pmatrix}
(−adg0b−e1−g01−a−b1−d−e01)\begin{pmatrix} -a&d&g&0\\ b&-e&1-g&0\\1-a-b&1-d-e&0&1\end{pmatrix}
(−ad1−f0b1−d0hc0fh−1)\begin{pmatrix}-a&d&1-f&0\\b&1-d&0&h\\c&0&f&h-1\end{pmatrix}
(0ff01−f1−ff−11−f−f00f)\begin{pmatrix}0&f&f&0\\1-f&1-f&f-1&1-f\\ -f&0&0&f\end{pmatrix}
再分别根据任意两行之间正交和行向量长度都相等可以得出约束方程求解，最后可以得出只有第一种可以使得行向量长度最大 这时b满足方程16b4+8b3−23b2+14b−2=016b^4+8b^3-23b^2+14b-2=0, 数字结果为e=b=0.20490155350665129314330190383234265145e=b=0.20490155350665129314330190383234265145，a=d=0.082734498297453867827044842101191253555,g=0.96486035057909231410839945902474434917a=d=0.082734498297453867827044842101191253555,g=0.96486035057909231410839945902474434917 对应边长的平方为1.0149247893784870917727027004682468871，于是d(3,4)为这个数的1.5次方。

类似经过一系列及其复杂的人机结合的运算，穷举分类d(3,n)可能出现的矩阵类型，得出d(3,n)的结论

n≡0(mod3)n\equiv 0(mod 3)， 最大棱长平方 n3\frac n3
n≡2(mod3)n\equiv 2(mod 3), 已知最大棱长平方n−23+0.20204102886728760721086370117643443213\frac{n-2}3+0.20204102886728760721086370117643443213
n≡1(mod3)n\equiv 1(mod 3),
 当n≤4n\le 4时,已知最大棱长平方n−13+0.014924789378487091772702700468246887087\frac{n-1}3+0.014924789378487091772702700468246887087,
 而在n=7n=7时，已知最大棱长平方为n−13+0.030276368395549006911606670186456882565\frac{n-1}3+0.030276368395549006911606670186456882565
 而在n≥10n\ge 10时，已知最大棱长平方n−13+0.0333704529042344576650050707338027930\frac{n-1}3+0.0333704529042344576650050707338027930

最后他另外提供了一段C代码对上面结论再进行数值验算

#include <stdio.h>
#include <math.h>

#define MAXSOL   50
#define N 6
double solbuf[MAXSOL][N];
int solc;
#define A(i,j) a[(i)*N+(j)]
void solve(double *a, double *b)
{
    int i,j,k;
    for(i=0;i<N;i++){//in i column
       double maxv = -1.0;
       int index=-1;
       for(j=i;j<N;j++){
          if(fabs(A(i,j))>maxv){
              maxv=fabs(A(i,j));
              index = j;
          }
       }
       if(index != i){//swap row index and i
         double tmp;
         for(j=i;j<N;j++){
             tmp = A(i,j);
             A(i,j)=A(index,j);
             A(index,j)=tmp;
         }
         tmp = b[i];
         b[i]= b[index];
         b[index]=tmp;
       }
       //divid by A(i,i) in row i
       for(j=i+1;j<N;j++)A(i,j)/=A(i,i);
       b[i]/=A(i,i);A(i,i)=1.0;
       for(j=0;j<N;j++){
          if(j==i)continue;
          for(k=i+1;k<N;k++){
             A(j,k)-=A(i,k)*A(j,i);
          }
          b[j]-=b[i]*A(j,i);
          A(j,i)=0.0;
       }
    }
}

void init_b(double *b, double x0, double y0, double z0, double a0, double b0, double c0, int N1, int N2)
{
    b[0]=x0+y0+z0-1.0;
    b[1]=x0*y0-a0*(1-a0);
    b[2]=y0*z0-b0*(1-b0);
    b[3]=z0*x0-c0*(1-c0);
    b[4]=x0*x0+a0*a0+(1-c0)*(1-c0)-y0*y0-(1-a0)*(1-a0)-b0*b0-N1;
    b[5]=x0*x0+a0*a0+(1-c0)*(1-c0)-z0*z0-(1-b0)*(1-b0)-c0*c0-N2;
}

void init_a(double *a, double x0, double y0, double z0, double a0, double b0, double c0,int N1, int N2)
{
    A(0,0)=1.0;A(0,1)=1.0;A(0,2)=1.0;A(0,3)=0.0;A(0,4)=0.0;A(0,5)=0.0;
    A(1,0)=y0;A(1,1)=x0;A(1,2)=0.0;A(1,3)=-1.0+2*a0;A(1,4)=0.0;A(1,5)=0.0;
    A(2,0)=0.0;A(2,1)=z0;A(2,2)=y0;A(2,3)=0.0;A(2,4)=-1+2*b0;A(2,5)=0.0;
    A(3,0)=z0;A(3,1)=0.0;A(3,2)=x0;A(3,3)=0.0;A(3,4)=0.0;A(3,5)=-1+2*c0;
    A(4,0)=2*x0;A(4,1)=-2*y0;A(4,2)=0.0;A(4,3)=2.0;A(4,4)=-2*b0;A(4,5)=-2+2*c0;
    A(5,0)=2*x0;A(5,1)=0.0;A(5,2)=-2*z0;A(5,3)=2*a0;A(5,4)=2-2*b0;A(5,5)=-2.0;
}

#define MAXITER 20
#define MINERR  0.00001
#define DELT    (4*MINERR)
void pushs(double x0, double y0,double z0, double a0,double b0,double c0)
{
    int i;
    for(i=0;i<solc;i++){
       if(fabs(x0-solbuf[i][0])<DELT&&fabs(y0-solbuf[i][1])<DELT&&
          fabs(z0-solbuf[i][2])<DELT&&fabs(a0-solbuf[i][3])<DELT&&
          fabs(b0-solbuf[i][4])<DELT&&fabs(c0-solbuf[i][5])<DELT){
            break;//find a matched solution
       }
    }
    if(i>=solc){
       if(solc>=MAXSOL){
          fprintf(stderr, "buffer overflow\n");
          return;
       }
       solbuf[solc][0]=x0;solbuf[solc][1]=y0;solbuf[solc][2]=z0;
       solbuf[solc][3]=a0;solbuf[solc][4]=b0;solbuf[solc][5]=c0;
       printf("x=%f,y=%f,z=%f,a=%f,b=%f,c=%f\n",
            x0,y0,z0,a0,b0,c0);
       solc++;
    }
}

int main(int argc, char *argv[])
{
    int N1=atoi(argv[1]);
    int N2=atoi(argv[2]);
    int count;
    double a1,b1,c1;
    double a[N*N],b[N];
    for(a1=0.1;a1<=0.9;a1+=0.1)for(b1=0.1;b1<=0.9;b1+=0.1)for(c1=0.1;c1<=0.9;c1+=0.1){
        double a0=a1,b0=b1,c0=c1,x0,y0,z0;
        double r=sqrt(a0*(1-a0)*b0*(1-b0)*c0*(1-c0));
        z0=r/(a0*(1-a0));x0=r/(b0*(1-b0));y0=r/(c0*(1-c0));
        if(0<x0&&x0<1&&0<y0&&y0<1&&0<z0&&z0<1){
          for(count=0;count<MAXITER;count++){
            init_a(a,x0,y0,z0,a0,b0,c0,N1,N2);
            init_b(b,x0,y0,z0,a0,b0,c0,N1,N2);
            solve(a,b);
            double maxerr=-1.0;
            int u;
            for(u=0;u<N;u++){
               if(fabs(b[u])>maxerr)maxerr=fabs(b[u]);
            }
            x0-=b[0];y0-=b[1];z0-=b[2];a0-=b[3];b0-=b[4];c0-=b[5];
            if(0<x0&&x0<1&&0<y0&&y0<1&&0<z0&&z0<1&&
                0<a0&&a0<1&&0<b0&&b0<1&&0<c0&&c0<1){
                 if(maxerr<MINERR){
                     
                     pushs(x0,y0,z0,a0,b0,c0);
                     break;
                 }
            }else{
                break;
            }
          }
        }
    }
}

至此，我们解决了超立方体嵌入最大三维立方体，但是嵌入更高维子立方体问题还有待大家的继续努力,按照上面的方法，对计算量要求会很大。

Github