谢尔宾斯基铜钱

Fri, 13th December 2019Edit on Githubcoin fractal 铜钱分形

摘要

KeyTo9_Fans在2017年9月提出一个问题：
我们把边长为1的正方形挖成谢尔宾斯基地毯，如下图所示： xebsj1

我们假设这个地毯的“面积”为1，

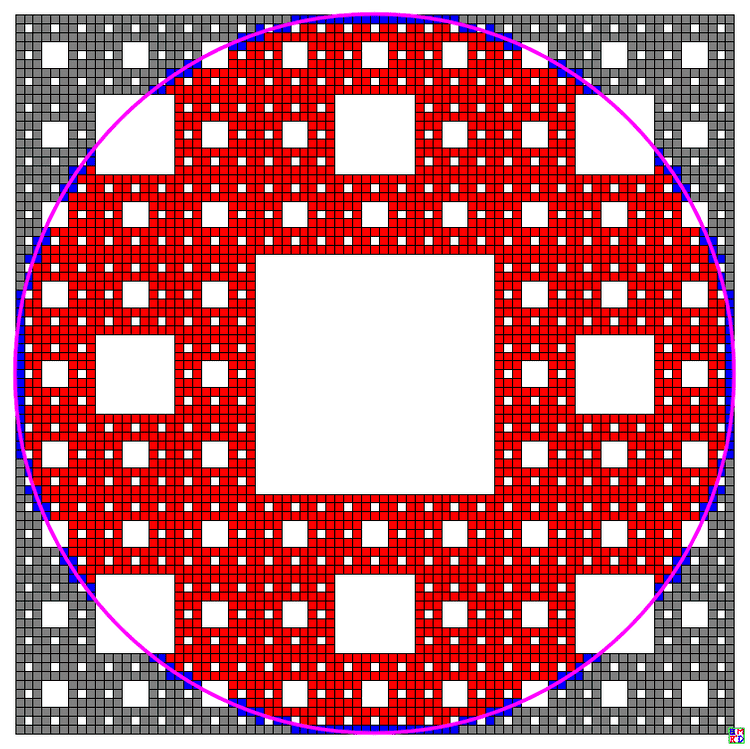
然后把该地毯“裁剪”成直径为1的圆，变成“谢尔宾斯基铜钱”，如下图红色部分所示： xebsj2

问：这个“谢尔宾斯基铜钱”的“面积是多少？

注：

严格来说，这不能称为【面积】，因为该地毯的维数不足2，其分形维只有 $\log_3 8=1.89...$ 维，是没有【面积】的。

这里的【面积】指的是豪斯多夫维积，也就是它在 $\log_3 8=1.89...$ 维空间里，所占空间的大小。

最后Ickiverar把谢尔宾斯基地毯计算到32层，使得我们可以得到21位有效精度的结果。

chyanog还把问题推广到三维情况，Ickiverar把这个问题也计算到了18层。

详细内容

对于这个题目，hujunhua首先给出了自己的看法 :
待我有空了，编个M10程序来计算一下这个孔方兄的“面积”。初步设想是这样的：
1、面积公式：将正方形划分成 $3^n\times 3^n$ 个小方块，则每个非白小方块的“面积”等于 $\frac1{8^n}$ 。设圆内的非白方块数为 $a(n)$ ,则孔方兄的“面积”大于并约等于 $\frac{a(n)}{8^n}$ 。
2、递进细分：把那些被圆周穿过的非白小方块扔到一个集C中，然后将集C中的每小方块划分为 $3\times 3$ 个更小的方块，设这些更小方块位于圆内的非白者数量为 $d(n)$ ，则孔方兄的面积增量等于 $\frac{d(n)}{8^{n+1}}$ 。
3、重复2. 直到达到指定的精度

mathe建议，由于图像上下左右的四块是一模一样的，我们只要看左下那四分之一部分。
wayne开始用Mathematica进行计算，不过开始出了点错。mathe建议同时统计正好落在圆上的小方块数目，就可以同时给出上下界了。hujunhua进一步建议取这个上下界的中值得出更好的估计值。
wayne使用了如下的代码

kernel=DeleteCases[Tuples[{-1,0,1},{2}],{0,0}];
kernel={{-1,-1},{0,-1},{1,-1},{1,0},{1,1},{0,1},{-1,1},{-1,0}};
rect={{-1,-1},{-1,1},{1,1},{1,-1}};
g[points_]:=Module[{ps=points},{Flatten[Table[Table[Join[k,{t=MinMax[Norm[ps[[2]]/6 #+k]&/@rect];(Sign[1/2-t[[1]]]+Sign[1/2-t[[2]]])/2}],{k,ps[[2]]/3 #+p[[1;;2]]&/@kernel}],{p,ps[[1]]}],1],ps[[2]]/3}]
pp=Nest[g,{{{0,0,1}},1},3];
Graphics[{EdgeForm[Thickness[.001]],Flatten[Table[{Which[j[[3]]==-1,Gray,j[[3]]==0,Blue,j[[3]]==1,Red],Rectangle[j[[1;;2]]+{-1,-1}*pp[[2]]/2,j[[1;;2]]+{1,1}*pp[[2]]/2]},{j,pp[[1]]}],1],Thickness[.005],RGBColor[1,0,1],Circle[{0,0},1/2]}]

给出了最初的结果,
统计所有的圆外，圆上，圆内的格子数目分别如下：

{{1},{1.},8}
{{1/16,7/16,1/2},{0.0625,0.4375,0.5},64}
{{13/64,19/128,83/128},{0.203125,0.148438,0.648438},512}
{{123/512,51/1024,727/1024},{0.240234,0.0498047,0.709961},4096}
{{259/1024,145/8192,5975/8192},{0.25293,0.0177002,0.72937},32768}
{{2117/8192,389/65536,48211/65536},{0.258423,0.00593567,0.735641},262144}
{{34119/131072,1045/524288,386767/524288},{0.26030731,0.0019931793,0.73769951},2097152}
{{547243/2097152,2801/4194304,3097017/4194304},{0.26094580,0.00066781044,0.73838639},16777216}

并且给出了两个不同分辨率的孔方兄快照
xebsj3
xebsj4

lsr314也给出了他的方案，不考虑与圆相交而被切割的误差，只以小正方形的中心位置来划分圆内圆外，那么可以用三进制来判断，代码如下：

f[x_, y_] :=
MemberQ[(IntegerDigits[Min[x, y], 3] - 1)^2 +
   Take[IntegerDigits[Max[x, y], 3] -
      1, -Length[IntegerDigits[Min[x, y], 3]]]^2, 0]
ff[l_] := (s = t = 0;
  Do[If[f[i, j], ,
    If[((i + 1/2)/3^l - 1/2)^2 + ((j + 1/2)/3^l - 1/2)^2 < 1/4,
     s = s + 1, t = t + 1]], {j, 0, 3^l - 1}, {i, 0, 3^l - 1}];
  s/(s + t))
Do[Print[{l, N[ff[l]]}], {l, 7}]

结果如下： {1,1.}
{2,0.8125}
{3,0.734375}
{4,0.742188}
{5,0.739502}
{6,0.738739}
{7,0.738728}

chyanog给出了两个版本的Mathematica代码
第一个需要11.1版本，使用了MengerMesh和计算几何相关的函数，代码简单易懂，不过效率不高

Clear["`*"];

n=3;

poly=MeshPrimitives[MengerMesh[n],2];

Graphics[{
Antialiasing->False,
EdgeForm[Black],
Red,Select[poly,RegionWithin[Disk[{0.5,0.5},0.5],#]&],
Blue,Select[poly,!RegionDisjoint[Circle[{0.5,0.5},0.5],#]&],
Gray,Select[poly,!RegionWithin[Disk[{0.5,0.5},0.5],#]&&RegionDisjoint[Circle[{0.5,0.5},0.5],#]&],
Thick,Magenta,Circle[{0.5,0.5},0.5]
}]

第二个版本速度快一些，不限于版本11

Clear["`*"];

carpet[n_]:=Nest[ArrayFlatten[{{#,#,#},{#,0,#},{#,#,#}}]&,1,n];

n=3;

ArrayPlot[carpet[n],Mesh->All]

p=Rescale[{{#1,#2},{#1+1,#2},{#1+1,#2+1},{#1,#2+1}}&@@@N@Position[carpet[n],1]];

Graphics[{
EdgeForm[Black],
Antialiasing->False,
Red,Polygon@Select[p,AllTrue[#,Norm[#-0.5]<0.5&]&],
Blue,Polygon@Select[p,With[{m=Norm[#-0.5]&/@#},Min@m<0.5&&Max@m>0.5]&],
Gray,Polygon@Select[p,AllTrue[#,Norm[#-0.5]>0.5&]&],
Thick,Magenta,Circle[{0.5,0.5},0.5]
}
]

补充内容 (2017-9-27 10:46):
次数，圆上，圆内，圆外，“面积”
{1, 8, 0, 0, 0.5}
{2, 28, 32, 4, 0.71875}
{3, 76, 332, 104, 0.72265625}
{4, 204, 2908, 984, 0.73486328125}
{5, 580, 23900, 8288, 0.73822021484375}

并且chyanog给出了几个小孔方兄的快照
xebsj5

hujunhua指出，当考察整个小方格是否位于圆内/外或者被圆穿越时，有没有人担心两个对顶格所公共的对顶格点刚好在圆上，使得两格刚好一内一外？或者像lsr314那样仅仅考察格子的中心时，有没有考虑过一个格子的中心刚好在圆上？
一个简单而有趣的事实是：无论分辨率多大，不可能有一个格子，它的中心或者一个顶点刚好在圆上。

wayne发现，其实这里面有大量的重复计算。当确定了某个正方形已经是整体的在圆内，或者圆外时，下一次迭代的时，由此产生的8个小正方形跟圆的关系没必要重复判断。我们只需进行简单的计数就行。这样程序只进行圆上的方格个数的统计。这样能大大的降低空间复杂度和时间复杂度。
然后他得到更新的结果

{{0,8,0},8,{0,1.0000000,0}}
{{4,28,32},64,{0.062500000,0.43750000,0.50000000}}
{{104,76,332},512,{0.20312500,0.14843750,0.64843750}}
{{984,204,2908},4096,{0.24023438,0.049804688,0.70996094}}
{{8288,580,23900},32768,{0.25292969,0.017700195,0.72937012}}
{{67744,1556,192844},262144,{0.25842285,0.0059356689,0.73564148}}
{{545904,4180,1547068},2097152,{0.26030731,0.0019931793,0.73769951}}
{{4377944,11204,12388068},16777216,{0.26094580,0.00066781044,0.73838639}}
{{35052688,29724,99135316},134217728,{0.26116288,0.00022146106,0.73861566}}
{{280499768,79276,793162780},1073741824,{0.26123577,0.000073831528,0.73869040}}
{{2244206376,212076,6345516140},8589934592,{0.26126001,0.000024688896,0.73871530}}
{{17954209288,565692,50764701756},68719476736,{0.26126813,8.2319020*10^-6,0.73872364}}

KeyTo9_Fans开始出手，一下子把迭代次数提升到18次

{0,8,0},8,{0.0000000000000000,1.0000000000000000,0.0000000000000000}
{4,28,32},64,{0.0625000000000000,0.4375000000000000,0.5000000000000000}
{104,76,332},512,{0.2031250000000000,0.1484375000000000,0.6484375000000000}
{984,204,2908},4096,{0.2402343750000000,0.0498046875000000,0.7099609375000000}
{8288,580,23900},32768,{0.2529296875000000,0.0177001953125000,0.7293701171875000}
{67744,1556,192844},262144,{0.2584228515625000,0.0059356689453125,0.7356414794921875}
{545904,4180,1547068},2097152,{0.2603073120117188,0.0019931793212891,0.7376995086669922}
{4377944,11204,12388068},16777216,{0.2609457969665527,0.0006678104400635,0.7383863925933838}
{35052688,29724,99135316},134217728,{0.2611628770828247,0.0002214610576630,0.7386156618595123}
{280499768,79276,793162780},1073741824,{0.2612357661128044,0.0000738315284252,0.7386904023587704}
{2244206376,212076,6345516140},8589934592,{0.2612600075080991,0.0000246888957918,0.7387153035961092}
{17954209288,565692,50764701756},68719476736,{0.2612681315513328,0.0000082319020294,0.7387236365466379}
{143635171632,1509332,406119132924},549755813888,{0.2612708551750984,0.0000027454589144,0.7387263993659872}
{1149085383304,4026028,3248957101772},4398046511104,{0.2612717669999256,0.0000009154127838,0.7387273175872906}
{9192693786392,10740796,25991667561644},35184372088832,{0.2612720716795138,0.0000003052717830,0.7387276230487032}
{73541578891856,28646804,207933369171996},281474976710656,{0.2612721732896830,0.0000001017738924,0.7387277249364246}
{588332707461496,76396620,1663467029827132},2251799813685248,{0.2612722071855238,0.0000000339269146,0.7387277588875616}
{4706661863240488,203728972,13307736442512524},18014398509481984,{0.2612722184847365,0.0000000113092298,0.7387277702060338}

hujunhua利用上面数据统计上下界的平均值，然后KeyTo9_Fans估计极限为0.738727775865795。

wayne随后表示还可以利用y=x的对称性于是只需要计算 $\frac1 8$ 的面积即可，他的代码由此突破了KeyTo9_Fans迭代18次的结果。
但是他的代码遇到了内存使用的瓶颈。后来他利用KeyTo9_Fans的代码并且略作修改使用2天12小时27分把结果迭代到了30次。

19: {37653295449008288,543283204,106461892083564380},{0.26127222225314139514,3.7697845123307871518*10^-9,0.73872777397707409253}
20: {301226365040331144,1448779164,851695138117736668},{0.26127222350931090383,1.2566156136484263328*10^-9,0.73872777523407348252}
21: {2409810924185402784,3863345612,6813561108806027412},{0.26127222392811149179,4.1886477055927406887*10^-10,0.73872777565302373765}
22: {19278487403784147304,10302538780,54508488880751520380},{0.26127222406771505802,1.3962543659240198024*10^-10,0.73872777579265950539}
23: {154227899257743649824,27473690092,436067911073488311796}
24: {1233823194135208730288,73263231116,3488543288661173252292}
25: {9870585553277031899992,195369181668,27908346309484760627908}
26: {78964684426737227956608,520985280228,223266770476399080439708}
27: {631717475415287101141792,1389296277316,1786134163812581951993244}
28: {5053739803326001562892000,3704793953044,14289073310504360438453772}
29: {40429918426617891895941808,9879454623900,114312586484044763011824820}
30: {323439347412969480294205216,26345219429236,914500691872384449385489772}

并且把极限估计到了0.73872777586246736918。

KeyTo9_Fans根据结果给出如下上下界
xebsj6
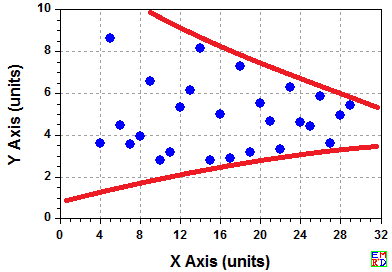
并预测20位有效结果为 $0.738727775862478009946(3)$

zeroieme也给出了一种横向分割的思路
 Ickiverar提供了一种思路避免int64之间的乘法并且提供了相应的C代码
并且在仅花费了1.6天就计算到了32层

{0, 8, 0}
{4, 28, 32}
{104, 76, 332}
{984, 204, 2908}
{8288, 580, 23900}
{67744, 1556, 192844}
{545904, 4180, 1547068}
{4377944, 11204, 12388068}
{35052688, 29724, 99135316}
{280499768, 79276, 793162780}
{2244206376, 212076, 6345516140}
{17954209288, 565692, 50764701756}
{143635171632, 1509332, 406119132924}
{1149085383304, 4026028, 3248957101772}
{9192693786392, 10740796, 25991667561644}
{73541578891856, 28646804, 207933369171996}
{588332707461496, 76396620, 1663467029827132}
{4706661863240488, 203728972, 13307736442512524}
{37653295449008288, 543283204, 106461892083564380}
{301226365040331144, 1448779164, 851695138117736668}
{2409810924185402784, 3863345612, 6813561108806027412}
{19278487403784147304, 10302538780, 54508488880751520380}
{154227899257743649824, 27473690092, 436067911073488311796}
{1233823194135208730288, 73263231116, 3488543288661173252292}
{9870585553277031899992, 195369181668, 27908346309484760627908}
{78964684426737227956608, 520985280228, 223266770476399080439708}
{631717475415287101141792, 1389296277316, 1786134163812581951993244}
{5053739803326001562892000, 3704793953044, 14289073310504360438453772}
{40429918426617891895941808, 9879454623900, 114312586484044763011824820}
{323439347412969480294205216, 26345219429236, 914500691872384449385489772}
{2587514779303826096159159104, 70253935029820, 7316005534979145849098804868}
{20700118234430796112810254760, 187343834543092, 58528044279833354136899152484}

据此KeyTo9_Fans给出了21位有效值估计 $0.7387277758624780099409(3)$ 。 KeyTo9_Fans把结果提交oeis形成了A293288 和A293289 。

三维扩展

chyanog建议再把问题推广到三维，
首先我们需要推广到门格海绵

然后他给出了对应的的门格海绵球的快照
xebsj7
hujunhua发现对于门格海绵球，会出现两个对顶小正方形正好分局分界球内外的情况（公共顶点在球面上），也会出现小正方体中心在球面的情况。
chyanog首先给出三维的计算结果
xebsj8
代码下载

2019年12月9日，Ickiverar给出了一个性能更高的C Source Code
并且在2019年12月13日计算到18层

迭代次数	球外	球上	球内的方块的个数
1	0	20	0
2	140	216	44
3	4456	1224	2320
4	97232	7968	54800
5	1999432	54456	1146112
6	40353584	367944	23278472
7	809527216	2444520	468028264
8	16206910376	16284576	9376805048
9	324246978160	108525168	187644496672
10	6485663211680	723469800	3753613318520
11	129718088017720	4822582872	75077089399408
12	2594393910475736	32150080560	1501573939443704
13	51888092541794104	214334797104	30031693123408792
14	1037763279756760904	1428893539656	600635291349699440
15	20755275121141905208	9525966857976	12012715352891236816
16	415105565929448931272	63506419362240	240254370564131706488
17	8302111741965441176320	423376135436184	4805087834658423387496
18	166042237661816931869288	2822507323770168	96101759515675744360544

结果被收集到A329302